Теория вероятностей – математическая наука, изучающая закономерности случайных явлений и событий, способных многократно повторяться при воспроизведении определенного комплекса условий.
Испытание – неопределяемое понятие, понимается как наблюдение того или иного явления. Событие – возможный исход того или иного испытания.
Определение1 : Результат наблюдения или эксперимента, который при данном испытании может произойти, а может и не произойти, называется случайным событием.
Определение2 : Событие, которое обязательно наступает при каждом испытании, называется достоверным.
Определение3 : Событие, которое заведомо не может произойти, называется невозможным.
Определение4 : Два события называются равносильными, если при каждом испытании они либо оба наступают, либо оба не наступают.
Определение5 : События, которые не могут произойти одновременно в результате испытания, называются несовместными.
Определение6 : Под множеством элементарных событий задачи понимают полное множество взаимоисключающих исходов эксперимента.
Пример: 1) Пусть эксперимент состоит в подбрасывании монеты. Два элементарных события: «выпадание орла» и «выпадание решки».
2) Пусть эксперимент состоит в подбрасывании кости. Шесть элементарных событий: выпадание единицы на верхней грани кости, выпадание двойки, тройки и т.д…
Определение7 (классическое определение вероятности) : Вероятностью события называется число, равное отношению числа исходов испытания, благоприятствующих событию (m) к числу всевозможных исходов испытания (n). Обозначается: P(A)= 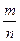 , P – вероятность случайного события, A – само событие.
, P – вероятность случайного события, A – само событие.
Пример: 1) Пусть эксперимент состоит в подбрасывании монеты. Два элементарных события: «выпадание орла» и «выпадание решки», значит n=2. Тогда вероятность события-«выпадание орла» равна P(A)= 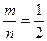 , где m=1.
, где m=1.
2) Пусть эксперимент состоит в подбрасывании кости. Шесть элементарных событий: выпадание единицы на верхней грани кости, и т.д… Вероятность события «выпадание шести очков на грани кости» равна P(A)= 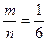 , где m=1.
, где m=1.
Определение 8. Событие (А и B), т. е. событие, состоящее в наступлении обоих событий А и B, называется произведением событий А и B и обозначается через
АB
Определение 9. Событие (А или B), т. е. событие, состоящее в наступлении хотя бы одного из событий А и B, называется суммой событий А и B и обозначается через
А + B
Теорема сложения вероятностей (для попарно несовместимых событий): вероятность того, что произойдет хотя бы одно из попарно несовместимых событий, равна сумме вероятностей этих событий P ( A + B + C ) = P ( A ) + P ( B ) + P ( C ).
Теорема произведения вероятностей (для попарно независимых событий): вероятность того, что произойдут одновременно независимые события, равна произведению вероятностей P ( A • B ) = P ( A ) • P ( B ).
Примеры решения задач
Задача 1. В двух коробках лежат карандаши. В первой коробке – 4 синих и 3 красных карандаша. Во второй коробке – 2 синих, 2 красных. Одновременно из двух коробок извлекают по одному карандашу. Найти вероятность того, что оба карандаша окажутся красными.
Решение: Пусть А- событие, что вынут красный карандаш из первой коробки. По классическому определению вероятности P(A)= 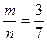 , где m=3, так как благоприятных исхода 3- в первой коробке 3 красных карандаша, а всего карандашей 7, значит n=7. Пусть В – событие, что вынут красный карандаш из второй коробки. Аналогично, P(В)=
, где m=3, так как благоприятных исхода 3- в первой коробке 3 красных карандаша, а всего карандашей 7, значит n=7. Пусть В – событие, что вынут красный карандаш из второй коробки. Аналогично, P(В)= 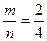 . Тогда по теореме произведения вероятностей, так как события происходят одновременно P ( A • B ) = P ( A ) • P ( B )=
. Тогда по теореме произведения вероятностей, так как события происходят одновременно P ( A • B ) = P ( A ) • P ( B )= 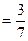
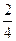 =
= 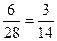 .
.
Дата: 2018-11-18, просмотров: 322.