1.1. Понятие множества, способы задания множеств
Определение 1. Множество есть любое собрание или совокупность различных между собой объектов. Эти объекты называются элементами или членами множеств.
Обозначатся множества большими буквами латинского алфавита A,B,C,D…, а элементы малыми (x 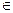 А. x
А. x 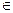 А).
А).
Примеры: 1. Множество студентов группы;
2. Множество R – всех действительных чисел

 Множества
Множества
Конечные – состоят из конечного Бесконечные
числа элементов.
Круги Эйлера
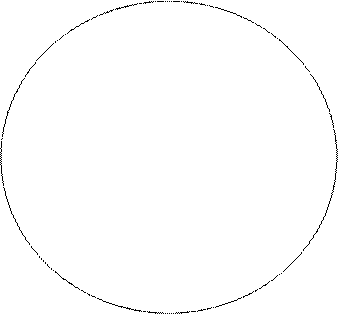
 R
R
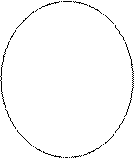 Q
Q
Z 
 I
I
N
C
N – множество натуральных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
I - множество иррациональных чисел;
R – множество действительных чисел;
С – множество комплексных чисел.
Способы задания множеств
Перечисление элементов.
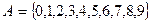 порядок перечисления элементов значения не имеет.
порядок перечисления элементов значения не имеет.
Указание характеристического свойства.
В множестве всех четных чисел (чисел, делящихся на 2).
 Читается:
Читается:
Множество В состоит из элементов x-целых чисел, таких, что x делится на 2.
-2 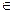 B; 7
B; 7 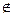 B.
B.
Операции над множествами.
Определение 2. Пересечением множеств А и В называется множество, состоящее из всех элементов принадлежащих каждому из множеств А и В, т.е.одновременно принадлежащих и множеству А и множеству В.
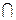 - знак пересечения
- знак пересечения
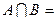 {x/x
{x/x 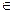 A и x
A и x 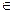 B}.
B}.
A B 


 N – конъюнкция «и» .
N – конъюнкция «и» .
 x
x 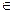 A
A 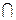 B
B 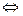 x
x 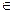 A
A 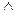 x
x 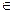 B;
B;
x 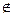 A
A 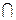 B
B 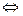 x
x 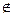 A
A 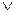 x
x 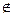 B.
B.
Определение 3. Объединением множеств A и B называется множество состоящие из элементов принадлежащих хотя бы одному из множеств А и В, т.е. или множеству А или множеству В.
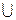 - знак объединения
- знак объединения

 А В
А В

 А
А 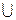 В = {x/ х
В = {x/ х 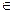 А
А 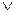 х
х 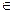 В}.
В}.
 х
х 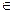 А
А 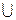 В
В 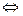 х
х 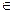 А
А 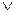 х
х 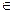 В
В
х 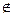 А
А 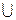 В
В 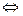 х
х 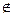 А
А 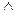 х
х 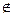 В
В
Определение 4. Разностью множеств А и В называется множество состоящее из элементов принадлежащих только множеству А.
\ - знак разности
А В


 А \В ={x / x
А \В ={x / x 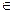 A
A 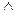 x
x 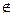 B}.
B}.

 x
x 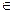 A \B
A \B 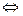 x
x 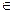 A
A 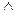 x
x 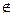 B.
B.
x 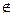 A \ B
A \ B 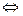 x
x 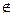 A
A 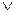 x
x 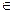 B.
B.
Определение 5. Дополнение множества А называется множество, состоящие из элементов х 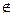 А.
А.
С - знак дополнения
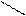





 СА
СА 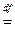 {x / x
{x / x 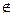 A}. А
A}. А
x 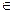 CA
CA 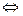 x
x 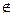 A
A




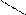 x
x 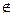 CA
CA 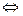 x
x 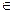 A.
A.
Примеры решения задач
Задача 4.1. Задать с помощью перечисления элементов множества 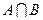 ,
, 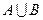 ,
, 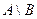 ,
, 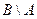 , если
, если 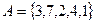 ,
, 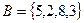 .
.
Решение. Пользуясь только определениями операций объединения, пересечения, разности множеств, получаем:
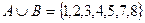 - множество - объединение множеств А и В, состоящее из элементов принадлежащих хотя бы одному из множеств А или В.
- множество - объединение множеств А и В, состоящее из элементов принадлежащих хотя бы одному из множеств А или В.
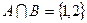 - множество - пересечение множеств А и В, состоящее из элементов, принадлежащих одновременно каждому из множеств А и В.
- множество - пересечение множеств А и В, состоящее из элементов, принадлежащих одновременно каждому из множеств А и В.
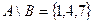 - множество – разность множеств А и В, состоящее из элементов, принадлежащих множеству А, но не принадлежащих множеству В.
- множество – разность множеств А и В, состоящее из элементов, принадлежащих множеству А, но не принадлежащих множеству В.
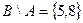 - множество - разность множеств В и А, состоящее из элементов, принадлежащих множеству В, но не принадлежащих множеству А.
- множество - разность множеств В и А, состоящее из элементов, принадлежащих множеству В, но не принадлежащих множеству А.
Задача 4.2. Заданы множества 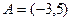 и
и 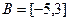 . Найти
. Найти  ,
,  ,
, 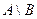 ,
, 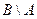 .
.
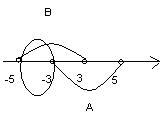
Решение. Множества А и В являются подмножествами множества действительных чисел R и называются промежутками. Их можно задать с помощью неравенств:
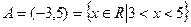 - промежуток не включает свои концы – числа -3 и 5. Такой промежуток называется интервалом.
- промежуток не включает свои концы – числа -3 и 5. Такой промежуток называется интервалом.
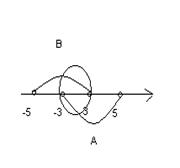
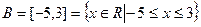 - промежуток включает свои концы – числа -5 и 3. Такой промежуток называется отрезком.
- промежуток включает свои концы – числа -5 и 3. Такой промежуток называется отрезком.
Пересечение 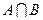 является полуинтервал
является полуинтервал
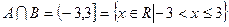 , где число -3 не принадлежит множеству А, а значит и пересечению
, где число -3 не принадлежит множеству А, а значит и пересечению 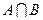 , число 3 принадлежит и множеству В и множеству А.
, число 3 принадлежит и множеству В и множеству А.
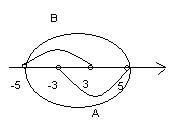
Объединение  является полуинтервал
является полуинтервал
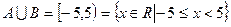 , где число -5 принадлежит уже хотя бы множеству В, а значит и объединению множеств, число 5 не принадлежит ни множеству А ни множеству В.
, где число -5 принадлежит уже хотя бы множеству В, а значит и объединению множеств, число 5 не принадлежит ни множеству А ни множеству В.
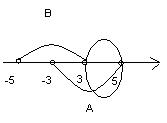
Разность множеств 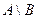 является интервал
является интервал
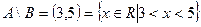 , где число 3 не принадлежит разности, так как принадлежит множеству В.
, где число 3 не принадлежит разности, так как принадлежит множеству В.
Разность множеств 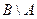 является отрезок
является отрезок
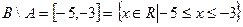 , где числа -5 и -3 принадлежит разности, так как принадлежит множеству В, и не принадлежат множеству А.
, где числа -5 и -3 принадлежит разности, так как принадлежит множеству В, и не принадлежат множеству А.
Дата: 2018-11-18, просмотров: 378.