ГЛАВНОЕ УПРАВЛЕНИЕ ОБРАЗОВАНИЯ И МОЛОДЕЖНОЙ ПОЛИТИКИ АЛТАЙСКОГО КРАЯ
КРАЕВОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«АЛТАЙСКИЙ ГОСУДАРСТВЕННЫЙ КОЛЛЕДЖ»
(КГБОУ СПО «Алтайский государственный колледж»)
Математика: методические указания и контрольные задания
для студентов заочной формы обучения
Специальность: 051001 «Профессиональное обучение»
(по отраслям)
Техническое обслуживание и ремонт автомобильного транспорта»
Барнаул 2012 г.
| Обсуждено на заседании ЦМК психолого-педагогических дисциплин Протокол № ____ от ________ «____» ____________ 20____г. Председатель ЦМК _____________ О.М. Кузеванова | Утверждено «____» ____________ 20___ г. Зав. заочным отделением ____________ Н.К.Кононова |
Поляничко О.Ю.
Математика: методические указания и контрольные задания для студентов: Учебное пособие для средних профессиональных учебных заведений.
Рецензент: Одинцова Л.А. – заведующая кафедрой математического анализа факультета математики и информатики Алтайской государственной педагогической академии, канд. пед. наук, профессор.
Настоящая методическая разработка представляет методические указания к выполнению домашней контрольной работы, содержащие краткий теоретический материал, примеры решения типовых задач и контрольные задания, предлагаемые студенту для самостоятельного решения, по темам «Элементы теории множеств», «Элементы линейной и векторной алгебры», «Дифференциальное и интегральное исчисление функции одной переменной», «Элементы теории вероятностей и математической статистики».
Методическая разработка предназначена для студентов-заочников средних профессиональных учебных заведений по специальностям 051001 «Профессиональное обучение» (по отраслям), 190631 «Техническое обслуживание и ремонт автомобильного транспорта».
Содержание
Введение................................................................................................... 4
Тема 1. Элементы теории множеств........................................................ 5
1.1. Понятие множества, способы задания множеств..................... 5
1.2. Примеры решения задач........................................................... 7
Тема 2. Элементы линейной алгебры..................................................... 8
2.1. Понятие матрицы, операции над матрицами........................... 8
2.2. Примеры решения задач........................................................... 9
Тема 3. Элементы векторной алгебры.................................................... 10
3.1. Вектор на плоскости.................................................................. 10
3.2. Примеры решения задач.......................................................... 11
Тема 4. Дифференциальное исчисление................................................. 11
4.1. Понятие производной функции................................................ 11
4.2. Примеры решения зада............................................................. 13
Тема 5. Интегральное исчисление........................................................... 14
5.1. Первообразная и неопределенный интеграл........................... 14
5.2. Примеры решения задач........................................................... 15
Тема 6. Элементы теории вероятностей................................................. 16
6.1. Понятие вероятности случайного события.............................. 16
6.2. Примеры решения задач........................................................... 18
Тема 7. Элементы математической статистики....................................... 18
7.1. Основные понятия..................................................................... 18
7.2. Примеры решения задач........................................................... 19
Контрольные задания.............................................................................. 20
Литература............................................................................................... 24
Приложения............................................................................................. 25
ВВЕДЕНИЕ
По дисциплине «Математика» студенты должны выполнить одну домашнюю контрольную работу. Контрольная работа выполняется в тетради и высылается в колледж для проверки. Без зачетной контрольной работы студент не допускается к экзамену. Контрольная работа включает в себя выполнение семи задач, которые составляют один из вариантов. Номер варианта контрольной работы определяется по двум последним цифрам индивидуального шифра студента.
При выполнении контрольной работы необходимо соблюдать следующие требования:
· условия каждой задачи переписываются полностью;
· текст домашней контрольной работы должен быть написан четко и разборчиво;
· строчки необходимо располагать через одну клетку;
· решение задачи должно сопровождаться соответствующими пояснениями со ссылкой на те формулы, которые используются;
· на каждой странице оставляется поле шириной 3-4 см для замечаний преподавателя, проверяющего работу.
В конце работы приводится список использованной литературы, в котором указываются те источники, по которым работа выполнялась, ставится подпись исполнителя и оставляется место для рецензии преподавателя.
Домашняя контрольная работа оценивается «зачтено» или «не зачтено». «Зачет» выставляется студенту в том случае, если выполнено 70% заданий и выше перечисленных требований. В остальных случаях ставится «незачет».
Зачтенная домашняя контрольная работа предъявляется студентом на экзамене. Незачтенные контрольные работы подлежат повторному выполнению. Задания не своего варианта не засчитываются и возвращаются студенту.
На обложке тетради указываются учебный шифр, наименование дисциплины, курс, отделение, номер учебной группы, фамилия, имя и отчество исполнителя, точный почтовый адрес.
В установленные учебным графиком сроки студент направляет выполненную работу для проверки в учебное заведение. После получения проверенной работы (с рецензией преподавателя) студенту необходимо исправить выявленные ошибки, выполнить все указания преподавателя. Усвоить успешно материал помогут схемы, алгоритмы составления которых и примеры указаны в приложении.
Если студент не может самостоятельно справиться с решением какой-либо задачи, он должен обратиться за консультацией к ведущему преподавателю в колледж.
Перечисление элементов.
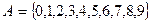порядок перечисления элементов значения не имеет.
Примеры решения задач
Задача 4.1. Задать с помощью перечисления элементов множества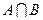 
, 
, 
, 
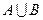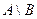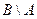, если 
, 
.
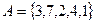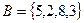Решение. Пользуясь только определениями операций объединения, пересечения, разности множеств, получаем:
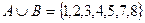- множество - объединение множеств А и В, состоящее из элементов принадлежащих хотя бы одному из множеств А или В.
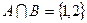- множество - пересечение множеств А и В, состоящее из элементов, принадлежащих одновременно каждому из множеств А и В.
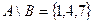- множество – разность множеств А и В, состоящее из элементов, принадлежащих множеству А, но не принадлежащих множеству В.
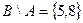- множество - разность множеств В и А, состоящее из элементов, принадлежащих множеству В, но не принадлежащих множеству А.
Задача 4.2. Заданы множества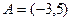 
и 
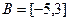. Найти , 
, , .
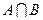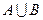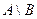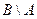Решение. Множества А и В являются подмножествами множества действительных чисел R и называются промежутками. Их можно задать с помощью неравенств:
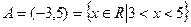- промежуток не включает свои концы – числа -3 и 5. Такой промежуток называется интервалом.
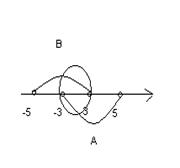
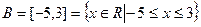- промежуток включает свои концы – числа -5 и 3. Такой промежуток называется отрезком.
Пересечение 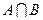является полуинтервал
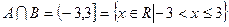, где число -3 не принадлежит множеству А, а значит и пересечению 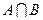, число 3 принадлежит и множеству В и множеству А.
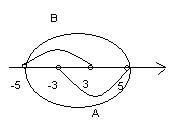
Объединение 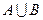является полуинтервал
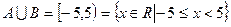, где число -5 принадлежит уже хотя бы множеству В, а значит и объединению множеств, число 5 не принадлежит ни множеству А ни множеству В.
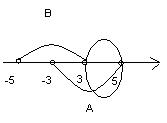
Разность множеств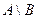 
является интервал
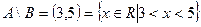, где число 3 не принадлежит разности, так как принадлежит множеству В.
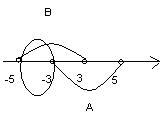
Разность множеств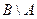 
является отрезок
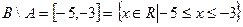, где числа -5 и -3 принадлежит разности, так как принадлежит множеству В, и не принадлежат множеству А.
Векторы на плоскости
Определение1 : Вектором называется направленный отрезок.
Обозначается латинскими буквами со стрелкой наверху: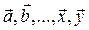 
.
Вектор, заданный парой (А, В) несовпадающих точек, обозначается символом 
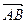. Точка А называется началом, а точка В – концом вектора.
Определение2 : Длиной (модулем) вектора 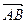называется расстояние между его началом и концом.
Обозначается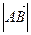 
. Вектор 
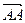, концы которого совпадают, называется нулевым вектором.
Пусть А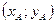 
, В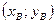 
Длина вектора 
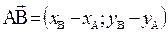находится по формуле 
.
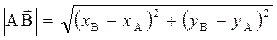Определение3: Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Обозначается символом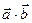 
. Таким образом, по определению,
.
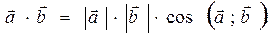Примеры решения задач
Задача 1. Найти длины и скалярное произведение векторов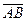 
, 
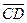, если известно 
, 
, 
, 
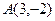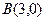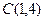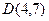, угол между векторами 
.
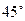Решение: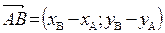 
. Тогда 
.
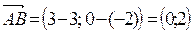Аналогично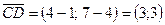 
.
Длина вектора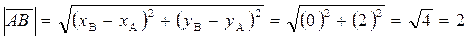 
Аналогично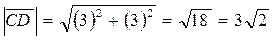 
.
Скалярное произведение векторов:
( 
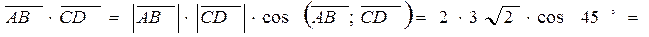
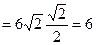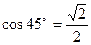). Ответ: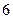 
Тема 4. Дифференциальное исчисление
Понятие производной функции
Определение1 : Производной функции f ( x ) в точке х0 называется предел (если он существует) отношения приращения функции ∆ f в этой точке к приращению аргумента ∆х, когда последнее стремится к нулю:
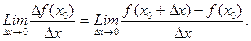
Обозначается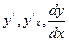 
или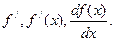 
Нахождение производной функции называется дифференцированием.
Определение2 : Дифференциалом функции f ( x ) называется произведение производной этой функции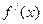 
на произвольное приращение аргумента.
Обозначается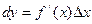 
или 
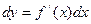, где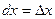 
.
Основные правила дифференцирования
1. Производная постоянной
Символьная формулировка: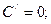 
Словесная формулировка: производная постоянной равна нулю.
2. Производная алгебраической суммы функций
Символьная формулировка: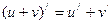 
Словесная формулировка: производная алгебраической суммы функций равна сумме производных этих функций.
3. Производная произведения двух функций
Символьная формулировка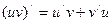 
Словесная формулировка: производная произведения двух функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго.
4. Производная произведения постоянной на функцию:
Символьная формулировка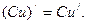 
Словесная формулировка: Постоянный множитель можно выносить за знак производной.
5. Производная частного двух функций:
Символьная формулировка: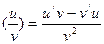 
6. Производная сложной функции:
Пусть y есть функция от u: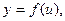 
а переменная u, в свою очередь, есть функция от аргумента х: 
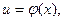т.е. если у зависит от х через промежуточный аргумент u, то у называется сложной функцией от х (функцией от функции):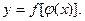 
Символьная формулировка: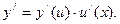 
Словесная формулировка: Производная сложной функции равна производной данной функции по промежуточному аргументу, умноженной на производную самого промежуточного аргумента по независимой переменной х:
Таблица производных элементарных функций
| Функция у | Производная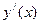 
|
| С | 0 |
| х | 1 |
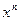для сложной функции: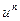 
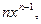|  где n – любое действительное число
|
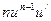
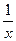для сложной функции: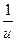 
| 
|
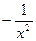
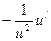
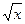для сложной функции: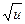 
| 
|
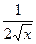
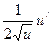
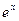для сложной функции: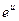 
|
|
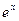
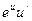
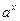для сложной функции: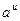 
| 
|
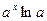
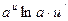
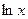для сложной функции: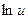 
|
|
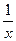
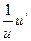
| Функция у | Производная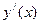
|
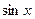для сложной функции: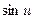 
| 
|
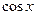
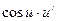
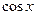для сложной функции: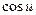 
| 
|
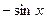
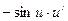
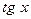для сложной функции: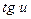 
| 
|
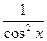
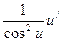
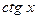для сложной функции: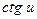 
| 
|
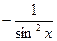
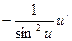
Примеры решения задач
Задача 1.
Объем продукции u (ед), произведённый бригадой рабочих, может быть описан уравнением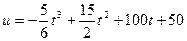 
(ед), 
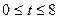, где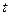 
-рабочее время, часы. Вычислить производительность труда, скорость и темп ее изменения через час после начала работы и за час до ее окончания.
Решение. Производительность труда выражается производной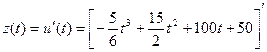 
. Используя правило нахождения производной суммы функций – 
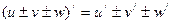, получим
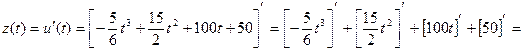. Используя правила нахождения производной произведения постоянной на функцию: 
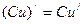, производной степенной функции 
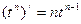, производной константы: 
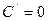имеем:
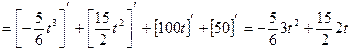
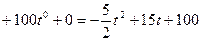(ед/ч)
Скорость изменения производительности – производная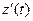 
. Темп изменения производительности – логарифмическая производная 
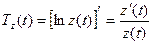(используем правило вычисления производной сложной функции, где 
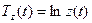)- сложная функция).
Найдем :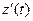 
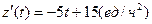(см. выше правила нахождения производной функции).
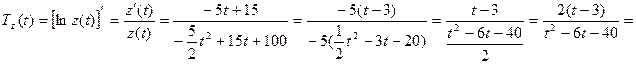
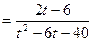(ед/ч).
В заданные моменты времени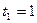 
и 
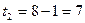соответственно имеем:
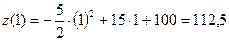(ед/ч), 
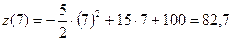(ед/ч),
, 
,
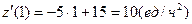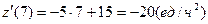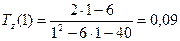(ед/ч), 
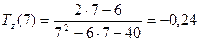(ед/ч).
Итак, к концу работы производительность труда существенно снижается, при этом изменение знака 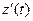и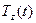 
с плюса на минус свидетельствует о том, что увеличение производительности труда в первые часы рабочего дня сменяется ее снижением в последние часы.
Задача 2. Найти дифференциал функции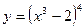 
Решение. По определению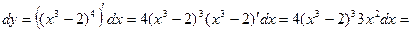 
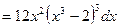(использовали правило нахождения сложной функции 
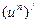см. таблицу 
= 
).
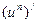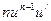Примеры решения задач
Задача 1. Найти интеграл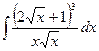 
Решение. При нахождении интегралов, подынтегральные функции которых содержат степенные функции, необходимо помнить, что (по определению)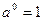 
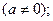
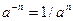
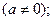
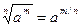
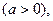
и знать следующие правила действия со степенями и корнями:
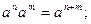
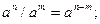
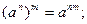
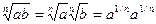
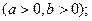
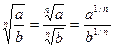
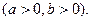
Здесь m и n – любые рациональные числа.
Преобразуем подынтегральную функцию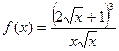 
: воспользуемся формулой сокращенного умножения 
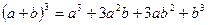и последующим почленным делением числителя на знаменатель.
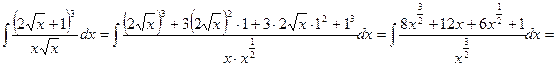
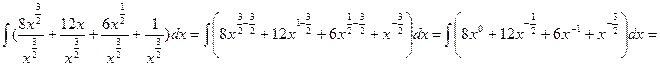Далее используем свойства неопределенного интеграла:
, 
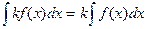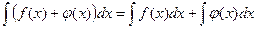и
табличные интегралы: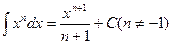 
, 
, 
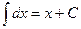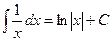. Имеем:
.
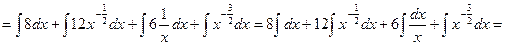
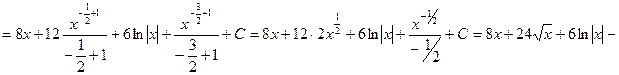
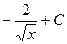Примеры решения задач
Задача 1. В двух коробках лежат карандаши. В первой коробке – 4 синих и 3 красных карандаша. Во второй коробке – 2 синих, 2 красных. Одновременно из двух коробок извлекают по одному карандашу. Найти вероятность того, что оба карандаша окажутся красными.
Решение: Пусть А- событие, что вынут красный карандаш из первой коробки. По классическому определению вероятности P(A)=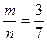 
, где m=3, так как благоприятных исхода 3- в первой коробке 3 красных карандаша, а всего карандашей 7, значит n=7. Пусть В – событие, что вынут красный карандаш из второй коробки. Аналогично, P(В)= 
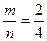. Тогда по теореме произведения вероятностей, так как события происходят одновременно P ( A • B ) = P ( A ) • P ( B )=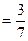 
= 
.
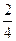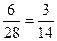Основные понятия
Математическая статистика – это раздел современной теории вероятностей, посвященный математическим методам систематизации, обработки и использования данных, полученных в результате экспериментов, для научных и практических выводов.
Определение 1. Генеральной совокупностью называется совокупность объектов, из которых производится выборка.
Определение 2. Выборкой называется совокупность случайно отобранных объектов.
Определение 3. Объемом выборки называется число объектов, заключенных в данной выборке,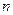 
.
Определение 4. Вариационным рядом выборки называется способ ее записи, при которой элементы упорядочиваются по величине, т.е. записываются в виде последовательности, где первый элемент – наименьший, а последующий за ним больше предыдущего.
Определение 5. Если выборка содержит одинаковые элементы и элемент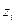 
встречается в ней 
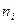раз, то число 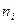называется частотой элемента .
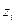Определение 6. Статистическим рядом (статистическим распределением выборки) называется перечень всех различных элементов выборки и соответствующих им частот:
| 
| 
| … | 
|
| 
| 
| … | 
|
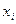
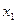
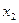
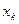
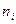
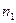
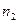
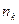
Определение 7. Законом распределения выборки называется перечень всех различных элементов выборки и соответствующих им вероятностей:
| 
| 
| … | 
|
| 
| 
| … | 
|
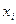
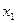
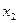
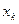
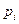
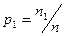
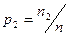
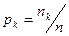
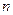- объем выборки, 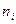- количество одинаковых элементов 
.
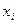Определение 8. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее значений на вероятности этих значений.
Обозначается: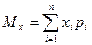 
.
Определение 9. Выборочной средней вариационного ряда называется среднее арифметическое значение выборочной совокупности.
Обозначается: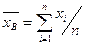 
.
Примеры решения задач
Задача. В результате десяти опытов получена следующая выборка: 2,2,3,4,2,4, 6,6,6,6. Найти объем выборки, вариационный ряд выборки, статистический ряд выборки, закон распределения выборки, математическое ожидание и выборочную среднюю вариационного ряда.
Решение: Объем выборки равен 10, так как 10 элементов. Упорядочим элементы и получим вариационный ряд выборки: 2,2,2,3,4,4,6,6,6,6.
Статистический ряд выборки:
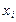
| 2 | 3 | 4 | 6 |
|
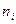
| 3 | 1 | 2 | 4 |
Закон распределения выборки:
|
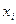
| 2 | 3 | 4 | 6 |
|
| 
| 
| 
| 
|
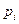
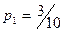
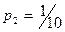
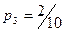
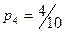
Математическое ожидание: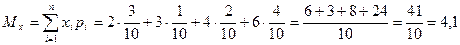 
.
Выборочная средняя вариационного ряда: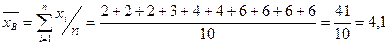 
Контрольные задания
Таблица
| № варианта | № задач | № вариан та | № задач | № вар иан та | № задач | № варианта | № задач | № варианта | № задач |
| 01 | 1,6,13,20, 26,36,41 | 21 | 5,12,14, 22,26,36,41 | 41 | 1,11,13, 24,26,36,41 | 61 | 4,10,14, 24,26,36,41 | 81 | 1,9,19, 20,26,36,41 |
| 02 | 2,7,14,21, 27,37,42 | 22 | 4,6,15,23, 27,37,42 | 42 | 2,12,14, 25,27,37,42 | 62 | 5,11,15, 25,27,37,42 | 82 | 2,10,18, 21,27,37,42 |
| 03 | 3,8,15,22, 28,38,43 | 23 | 3,7,16,24, 28,38,43 | 43 | 3,6,15,20, 28,38,43 | 63 | 1,12,16, 20,28,38,43 | 83 | 3,11,17, 22,28,38,43 |
| 04 | 4,9,16,23, 29,39,44 | 24 | 2,8,17,25, 29,39,44 | 44 | 4,7,16,21, 29,39,44 | 64 | 2,6,17,21, 29,39,44 | 84 | 4,12,16, 23,29,39,44 |
| 05 | 5,10,17,24, 30,40,45 | 25 | 1,9,18,20, 30,40,45 | 45 | 5,8,17,22, 30,40,45 | 65 | 3,7,18,22, 30,40,45 | 85 | 5,6,15, 24,30,40,45 |
| 06 | 2,11,18,25, 31,36,46 | 26 | 4,10,19, 21,31,36,46 | 46 | 2,9,18,23, 31,36,46 | 66 | 4,8,19,23, 31,36,46 | 86 | 1,7,14, 25,31,36,46 |
| 07 | 3,12,19,20, 32,37,47 | 27 | 3,11,13, 22,32,37,47 | 47 | 3,10,19, 24,32,37,47 | 67 | 5,9,13,24, 32,37,47 | 87 | 2,8,13, 20,32,37,47 |
| 08 | 4,6,14,21, 33,38,48 | 28 | 2,12,19, 23,33,38,48 | 48 | 4,11,13, 25,33,38,48 | 68 | 1,10,14, 25,33,38,48 | 88 | 3,9,19, 21,33,38,48 |
| 09 | 5,7,15,22, 34,39,49 | 29 | 1,6,18,24, 34,39,49 | 49 | 5,12,14, 20,34,39,49 | 69 | 2,11,15, 20,34,39,49 | 89 | 4,10,18, 22,34,39,49 |
| 10 | 1,8,16,23, 35,40,50 | 30 | 5,7,17,25, 35,40,50 | 50 | 1,6,15,21, 35,40,50 | 70 | 3,12,16, 21,35,40,50 | 90 | 5,11,17, 23,35,40,50 |
| 11 | 3,9,17,24, 26,36,50 | 31 | 3,8,16,20, 26,36,50 | 51 | 3,7,16,22, 26,36,50 | 71 | 4,6,17,22, 26,36,50 | 91 | 1,12,16, 24,26,36,50 |
| 12 | 4,10,18,25, 27,37,49 | 32 | 2,9,15,21, 27,37,49 | 52 | 4,8,17,23, 27,37,49 | 72 | 5,7,18,23, 27,37,49 | 92 | 2,6,15, 25,27,37,49 |
| 13 | 5,11,19,20, 28,38,48 | 33 | 1,10,14, 22,28,38,48 | 53 | 5,9,18,24, 28,38,48 | 73 | 1,8,19,24, 28,38,48 | 93 | 3,7,14, 20,28,38,48 |
| 14 | 1,12,13,21, 29,39,47 | 34 | 5,11,19, 23,29,39,47 | 54 | 1,10,19, 25,29,39,47 | 74 | 2,9,13,25, 29,39,47 | 94 | 4,8,13, 21,29,39,47 |
| 15 | 2,6,15,22, 30,40,46 | 35 | 4,12,13, 24,30,40.46 | 55 | 2,11,15, 20,30,40,46 | 75 | 3,10,14, 20,30,40,46 | 95 | 5,9,19, 22,30,40,46 |
| 16 | 4,7,16,23, 31,36,45 | 36 | 2,6,14,25, 31,36,45 | 56 | 4,12,16, 21,31,36,45 | 76 | 5,11,15, 21,31,36,45 | 96 | 1,10,18, 23,31,36,45 |
| 17 | 5,8,17,24, 32,37,44 | 37 | 1,7,15,20, 32,37,44 | 57 | 5,6,17,22, 32,37,44 | 77 | 4,12,16, 22,32,37,44 | 97 | 2,11,17, 24,32,37,44 |
| 18 | 1,9,18,25, 33,38,43 | 38 | 5,8,16,21, 33,38,43 | 58 | 1,7,18,23, 33,38,43 | 78 | 3,6,17,23, 33,38,43 | 98 | 4,12,16, 25,33,38,43 |
| 19 | 2,10,19,20, 34,39,42 | 39 | 4,9,17,22, 34,39,42 | 59 | 2,8,19,24, 34,39,42 | 79 | 1,7,18,24, 34,39,42 | 99 | 5,6,15, 20,34,39,42 |
| 20 | 3,11,13,21, 35,40,41 | 40 | 3,10,18, 23,35,40,41 | 60 | 3,9,13,25, 35,40,41 | 80 | 2,8,19,25, 35,40,41 | 00 | 1,7,14, 21,35,40,41 |
Задачи 1-5 Теория множеств
Заданы множества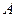 
и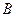 
. Найти 
, 
, 
, 
.
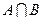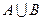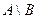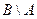1. Множества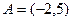 
и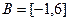 
.
2. Множества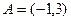 
и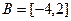 
.
3. Множества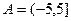 
и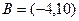 
.
4. Множества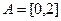 
и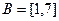 
.
5. Множества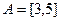 
и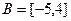 
.
Схемы
Денотатный граф
Алгоритм построения денотатного графа:
1. выделение ключевого слова – определяющего понятия - …(по вашему примеру)
2. чередование имени и глагола в графе – именем может быть одно существительное или группа существительных в сочетании с другими именными частями речи; глагол выражает динамику мысли, движение от понятия к его существенному признаку (перечислите глаголы, которые выделили или существительные – имена)
3. необходимо соблюдать точный выбор глагола (глаголы обозначающие цель – направлять, предполагать, приводить, давать…, глаголы, обозначающие процесс достижения результата – достигать, осуществляться, глаголы, обозначающие предпосылки достижения результата – основываться, базироваться, опираться; глаголы-связки, с помощью которых осуществляется выход на определение значения понятия)
4. дробление ключевого понятия по мере построения графа на слова – «веточки»- …
5. соотнесение каждого слова-«веточки» с ключевым словом с целью исключения каких-либо несоответствий, противоречий.
Дифференциальные уравнения.
ГЛАВНОЕ УПРАВЛЕНИЕ ОБРАЗОВАНИЯ И МОЛОДЕЖНОЙ ПОЛИТИКИ АЛТАЙСКОГО КРАЯ
КРАЕВОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«АЛТАЙСКИЙ ГОСУДАРСТВЕННЫЙ КОЛЛЕДЖ»
(КГБОУ СПО «Алтайский государственный колледж»)
Математика: методические указания и контрольные задания
для студентов заочной формы обучения
специальность: 051001 «Профессиональное обучение»
(по отраслям)
Дата: 2018-11-18, просмотров: 348.
