Пусть в т. 1 находится тело А с зарядом q1. - Потенциал его - 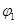 .Тогда емкость тела С1
.Тогда емкость тела С1 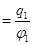 .
.
Поместим около него другое металлическое тело. Это тело заряжается через влияние. Обозначим заряды, созданные на теле В через -q2 и q3. Потенциалы этих зарядов в т. А обозначим - 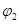 и +
и + 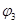 .
.

Тогда полный потенциал в т. А: 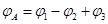
Теперь уже емкость тела А:
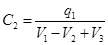 т. е. емкость тела А в присутствии тела В изменилась.
т. е. емкость тела А в присутствии тела В изменилась.
Ёмкость тела А в присутствии тела В всегда увеличивается.
Действительно, заряд 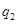 уменьшает потенциал тела А и увеличивает его емкость. Заряд
уменьшает потенциал тела А и увеличивает его емкость. Заряд 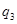 увеличивает потенциал тела А и уменьшает емкость. Но заряд
увеличивает потенциал тела А и уменьшает емкость. Но заряд 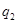 расположен ближе, потому его влияние сильнее.
расположен ближе, потому его влияние сильнее.
Это явление используется для создания систем с большой ёмкостью - конденсаторов.
Чтобы емкость конденсаторов не зависела от расположения окружающих предметов, необходимо обеспечить такую конструкцию конденсаторов, чтобы вне конденсатора поле его было равно нулю и конденсатор не электризовал окружающие предметы.
Виды конденсаторов
- Плоский конденсатор
Он представляет собой две плоскопараллельные пластины, расположенные на малом, по сравнению с размерами пластин расстояние друг от друга. На одной пластине заряд 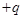 , на другой -равный ему по величине (-
, на другой -равный ему по величине (- 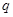 ). Емкость такой системы:
). Емкость такой системы:
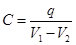 ,
,
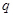 -абсолютное значение зарядов на пластине,
-абсолютное значение зарядов на пластине,
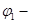 значение потенциала одной пластины,
значение потенциала одной пластины,
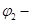 значение потенциала другой пластины,
значение потенциала другой пластины,
Выразим емкость через геометрические размеры конденсатора
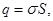 Е=
Е= 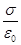
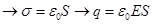
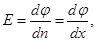 Е=
Е= 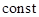
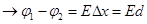
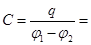
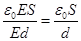 т.е.
т.е. 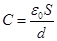
- Сферический конденсатор
Этот конденсатор - две концентрические сферы с радиусами 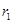 и
и 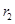 . Ёмкость этой системы
. Ёмкость этой системы
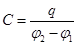
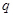 -абсолютное значение зарядов на сферах,
-абсолютное значение зарядов на сферах,
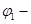 значение потенциала одной сферы,
значение потенциала одной сферы,
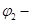 значение потенциала другой сферы,
значение потенциала другой сферы,
Выразим емкость через геометрические размеры конденсатора.
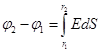
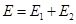
Е -напряженность в точках между двумя сферами,
Е1 - напряженность от сферы с радиусом 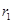
Е2 - напряженность от сферы с радиусом 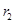
Помните: напряженность внутри полости от заряженной сферы равна нулю., поэтому в точках между двумя сферами Е2=0. Тогда:
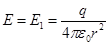 ,
, 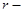 радиус-вектор рассматриваемой точки
радиус-вектор рассматриваемой точки
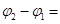
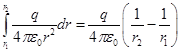 .
. 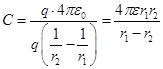
Цилиндрический конденсатор.
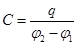 ,
, 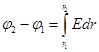 Напряженность между цилндрическими поверхностями совпадает с напряженностью от внутреннего цилиндра, т.е.
Напряженность между цилндрическими поверхностями совпадает с напряженностью от внутреннего цилиндра, т.е. 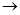
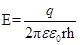 , где
, где 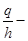 есть линейная плотность заряда
есть линейная плотность заряда 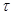 на цилиндре
на цилиндре
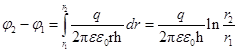 ,
, 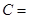
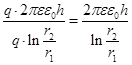
Далее желательно прочесть $ 26 "Соединение конденсаторов" Савельева (т.2 стр. 73  74)
74)
Лекция 5 (Продолжение)
Энергия электрического поля
Энергия системы неподвижных точечных зарядов. Энергия заряженного проводника, заряженного конденсатора. Объемная плотность энергии. Энергия электростатического поля.
Дата: 2018-11-18, просмотров: 741.