Закон Ома
1. Основной закон постоянного тока - закон Ома. Это экспериментальный закон.

Сила тока пропорциональна разности потенциалов на концах участка проводника. Проводник однородный, если в нем нет скачков потенциалов или нет эдс
R - коэффициент пропорциональности, называется сопротивлением.
2. Единица измерения сопротивления
СГСЕ: за единицу сопротивления принимается сопротивление проводника, в котором при разности потенциалов на концах в одну СГСЕ-единицу течет одна СГСЕ единица тока.
СИ: за единицу сопротивления принимается сопротивление проводника, в котором при разности потенциалов на концах в одн вольт возникает ток в один ампер.Это - Ом.
Связь между Омом и СГСЕ единицей сопротивления:
1 Ом= 
3. R зависит от:
· материала проводника
· его размеров
· его формы
Если площадь поперечного сечения  то
то
 , где
, где  длина проводника,
длина проводника,  удельное сопротивление, равное
удельное сопротивление, равное  ,
,
т.е. удельное сопротивление численно равно сопртивлению проводника, имеющего единицу длины и единицу площади поперечного сечения
Величина  определяется химической природой вещества, температурой
определяется химической природой вещества, температурой
 =
= 
 при обычной температуре (почти для всех металлов)
при обычной температуре (почти для всех металлов)
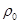 -уд. сопротивление при t=0 C
-уд. сопротивление при t=0 C
 коэффициент,
коэффициент,  .
.
При очень низких и высоких температурах это соотношение не выполняется. При температуре, равной нескольким градусам Кельвина, для большой группы металлов  скачком обращается в 0.
скачком обращается в 0.

Это явление сверхпроводимости,  температура перехода в состояние сверхпроводимости.
температура перехода в состояние сверхпроводимости.
Дифференциальная форма записи закона Ома для участка цепи.
Закон Ома  связывает величины, относящиеся к различным точкам проводника
связывает величины, относящиеся к различным точкам проводника 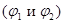 или к конечным участкам. Это закон Ома в интегральной форме.
или к конечным участкам. Это закон Ома в интегральной форме.
Дифференциальное уравнение должно связать характеристики одной точки проводника. Вокруг некоторой точки выделим элементарный цилиндрический объем.

Образующие 
Основание 


Для данного элементарного цилиндрического объема:

Направление  совпадает с направлением Е в данной точке, потому:
совпадает с направлением Е в данной точке, потому:

 плотность тока в данной точке,
плотность тока в данной точке,  напряженность поля в данной точке.
напряженность поля в данной точке.
Вывод: полученный закон Ома связывает характеристики одной точки, потому  - дифференциальная форма записи закона Ома.
- дифференциальная форма записи закона Ома.
Закон Джоуля-Ленца
Второй экспериментальный закон - закон Джоуля-Ленца

 количество тепла, выделяемого в проводнике
количество тепла, выделяемого в проводнике
 время, в течении которого выделялось тепло.
время, в течении которого выделялось тепло.
Как теоретически объяснить этот закон?

Если:
- проводник неподвижен
- не наблюдается химических реакций, то


Учтем:  т. е. совпадение с экспериментальным законом.
т. е. совпадение с экспериментальным законом.
 - интегральная форма записи закона Джоуля-Ленца.
- интегральная форма записи закона Джоуля-Ленца.
Найдем дифференциальную форму записи.
Опять вокруг т. А выделим элементарный объем - цилиндр.


 - количество теплоты, выделяющейся в единице объема в единицу времени - удельная мощность тока, тогда:
- количество теплоты, выделяющейся в единице объема в единицу времени - удельная мощность тока, тогда:
 , т.е.удельная мощность тока
, т.е.удельная мощность тока  и
и  .
.
 - дифференциальная форма записи закона Джоуля-Ленца.
- дифференциальная форма записи закона Джоуля-Ленца.
Сторонние электродвижущие силы 
Выяснили:
- перенос заряда по проводникам под действием Е сопровождается работой электрической силы
- эквивалентное этой работе количество энергии выделяется в форме джоулева тепла.
Вывод: для поддержания постоянного электрического тока необходима затрата энергии.
С другой стороны: поле постоянных токов потенциально. Следствие:  , т.е. работа электрических сил по замкнутому контуру равна 0.
, т.е. работа электрических сил по замкнутому контуру равна 0.
Вывод: в цепи постонного тока для его поддержания должна действовать сила неэлектростатического происхождения, работа которой по замкнутому контуру  и потому она может возмещать все потери энергии.
и потому она может возмещать все потери энергии.
При наличии одних кулоновских сил стационарное поле должно быть электростатическим
Т.к. положительные заряды движутся от т. с большим потенциалом к точкам с меньшим потенциалом, это приводит к выравниванию потенциалов, т.е. уничтожению причины движения.
Сила неэлектростатического происхождения, поддерживающая ток в цепи, называется сторонней силой  .
.
Можно записать выражение:

 напряженность поля сторонних сил
напряженность поля сторонних сил
Работа сторонних сил на участкет1-2:

Величина  , равная работе сторонних сил, отнесенной к единице положительного заряда, называется электродвижущей силой
, равная работе сторонних сил, отнесенной к единице положительного заряда, называется электродвижущей силой  . Обозначается
. Обозначается  буквой
буквой  .
.

Размерность  совпадает с размерностью потенциала.
совпадает с размерностью потенциала.
Если на заряд действует и электрическая сила и сторонняя, то 

Величина, численно равная работе, совершаемой электростатическими и сторонними силами при перемещении единичного положительного заряда, называется падением напряжения или просто напряжением  на данном участке пути
на данном участке пути


Закон Ома для неоднородного участка цепи
Неоднородный участок цепи - участок, на котором действует электродвижущая сила.
Если участок неоднородный, то 
Закон Ома:

 это закон Ома в дифференциальной форме для неоднородного участка.
это закон Ома в дифференциальной форме для неоднородного участка.
В интегральной форме
Возьмем участок проводника. Запишем для точки внутри него закон Ома в дифференциальной форме
 Умножим обе части равенства на
Умножим обе части равенства на 
 =
=  ;
;  ;
; 



 - закон Ома для неоднородного участка цепи в интегральной форме. Читается так: Произведение силы тока на
- закон Ома для неоднородного участка цепи в интегральной форме. Читается так: Произведение силы тока на  произвольного участка цепи равно напряжению, приложенному к заданному участку цепи.
произвольного участка цепи равно напряжению, приложенному к заданному участку цепи.
Если поле потенциально, то:

 или
или 
 - закон Ома.
- закон Ома.
Закон Ома для замкнутой цепи
Если точки 1 и 2 совпадают, т.е. 1=2, то:


Для электростатического поля  , потому
, потому

 ;
; 
 ;
; 
Сила неразветвленного постоянного тока равна частному от деления полной сторонней ЭДС в его цепи на сопротивление этой цепи.
При 

Разветвленные цепи. Правила Кирхгофа.
Обобщенный закон Ома для участка цепи

позволяет рассчитать любую сложную цепь. Однако непосредственный расчет сложных цепей довольно труден. Эта трудность в большой степени обходится, если пользоваться двумя правилами Кирхгофа, вытекающими из законов постоянного тока. Эти правила связывают силы токов, характеризующие отдельные участки цепи, их сопротивления и ЭDS, включенные в эти участки цепи.
Первое правило Кирхгофа
Оно относится к узлам цепи. Узел - это точка, в которой сходятся не меньше трех проводников цепи. Ток, текущий к узлу, считается положительным, а от узла - отрицательным.
Первое правило формулируется следующим образом: алгебраическая сумма сил токов, сходящихся в узле, равна нулю. Аналитически это записывается так:
 где
где  n - число токов, сходящихся в узле.
n - число токов, сходящихся в узле.
Обоснование этого правила
Т.к. ток в цепи постоянный, то в цепи должно оставаться неизменным распределение потенциалов между отдельными сечениями цепи. В таком случае потенциал узла остается неизменным во времени. Тогда остается неизменным и заряд узла. Но если это так, то подходящий к узлу заряд должен быть равен уходящему, потому алгебраическая сумма токов, подходящих к узлу, должна быть равна нулю.
Если в рассматриваемой системе n узлов, то независимых уравнений для токов можно составить (n-1), n-ое уравнение будет следствием (n-1) уравнений.
Второе правило Кирхгофа
В любом замкнутом контуре, произвольно выбранном в разветвленной цепи проводников, сумма произведений сил токов на сопротивление соответствующих участков цепи равна сумме ЭДС, встречающихся в этом контуре.
 где
где  число участков в замкнутом контуре, к - номер данного участка.
число участков в замкнутом контуре, к - номер данного участка.
Это правило является следствием обобщенного закона Ома для участка цепи. Покажем это на примере произвольного замкнутого контура
Обобщенный закон Ома для отдельных участков взятого контура:


Сложим левые и правые части этих равенств

 , получили правило Кирхгофа.
, получили правило Кирхгофа.
Такие уравнения можно составить для всех замкнутых контуров разветвленной цепи. Независимыми уравнениями будут только уравнения, составленные для тех контуров, которые не получаются в результате наложения уже рассмотренных. Итак: пользуясь првилами Кирхгофа, можно составить  уравнений.
уравнений.
 число узлов в разветвленной цепи
число узлов в разветвленной цепи
 число контуров, которые не получаются в результате наложения уже рассмотренных.
число контуров, которые не получаются в результате наложения уже рассмотренных.
Если число этих уравнений равно числу неизвестных, то правила Кирхгофа позволяют решить задачу.
Если число неизвестных больше, то некоторые из них не могут быть определены. Если число неизвестных меньше, то нужно составить необходимое число уравнений.
При развернутой записи уравнения второго правила Кирхгофа необходимо:
1. Выбрать определенное направление обхода замкнутого контура (например по часовой стрелке)
2. Считать положительными те токи, направление которых совпадает с направлением обхода и отрицательными те, направление которых противоположно направлению обхода
3. Считать положительными те ЭДС, которые повышают потенциал в направлении обхода. Т.к. ток течет от положительного полюса (1) к отрицательному(1), то потенциал положительного полюса выше потенциала отрицательного. Поэтому  нужно принимать положительной, если при обходе первым встречается отрицательный полюс.
нужно принимать положительной, если при обходе первым встречается отрицательный полюс.
Если не учесть верно знаки токов и ЭДС, решение окажется неверным.
Пример расчета разветвленной цепи с применением правил Кирхгофа

К одинаковых элементов с ЭДС  соединены параллельно
соединены параллельно
 внутреннее сопротивление каждого элемента
внутреннее сопротивление каждого элемента
 внешнее сопротивление, на которое замкнута батарея элементов.
внешнее сопротивление, на которое замкнута батарея элементов.
Сопротивлением соединительных проводов можно пренебречь. Определить силу тока  , протекающего по сопротивлению.
, протекающего по сопротивлению.
В данной цепи не известны величины: 
 ,
,  ,
,  ,
,  .
.
В цепи два узла. В этом случае можно составить одно независимое уравнение, допустим для узла А:
 . Токи
. Токи  ,
,  ,
,  - входят в узел, потому им приписываем знак "+". Ток
- входят в узел, потому им приписываем знак "+". Ток  выходит из узла, потому ему приписываем знак "-". тогда:
выходит из узла, потому ему приписываем знак "-". тогда:  +
+  +
+  -
-  =0. Т.к. участки А
=0. Т.к. участки А  В, А
В, А  2В и А
2В и А  абсолютно одинаковые, то
абсолютно одинаковые, то  =
=  =
=  . Тогда кi1=
. Тогда кi1= 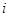
 .
.
Т.к. все четыре неизвестные величины сводятся к одной неизвестной, то достаточно составить одно уравнение по 2-у правилу Кирхгофа. С целью нахождения тока  удобно выбрать замкнутый контур
удобно выбрать замкнутый контур  . Контур будем обходить по часовой стрелке. Т.к. токи
. Контур будем обходить по часовой стрелке. Т.к. токи  1 и
1 и  противоположны направлению обхода, то берем их с отрицательными знаками, т.е.
противоположны направлению обхода, то берем их с отрицательными знаками, т.е.  .
.
При обходе по часовой стрелке ЭДС понижает потенциал, потому берем  с отрицательным знаком, т.е.
с отрицательным знаком, т.е.  . Тогда
. Тогда  т.к.
т.к.  , то
, то  ,
,  .
.
Эту формулу можно прочесть следующим образом: при параллельном соединении  одинаковых элементов в батарею, ЭДС не меняется, а внутреннее сопротивление уменьшается в
одинаковых элементов в батарею, ЭДС не меняется, а внутреннее сопротивление уменьшается в  раз.
раз.
Магнитное поле в веществе
Намагничивание вещества. Намагниченность. Связь векторов напряженности, индукции, намагниченности. Магнитная восприимчивость, магнитная проницаемость. Ларморовская прецессия электронных орбит. Диамагнетики, парамагнетики, ферромагнетики. Магнитный гистерезис, Закон Кюри-Вейса, точка Кюри.
До сих пор рассматривали магнитное поле в пустоте, т.е. в пространстве. в котором в достаточном количестве нет атомов и элементарных частиц. Теперь рассмотрим магнитное поле в веществе. Особый интерес представляют магнетики. Это вещества, способным влиять на магнитное поле или создавать магнитное поле.
Впервые, правильное объяснение природы магнетизма выдвинул Ампер. Он предположил, что поле намагниченных магнетиков, как и внешнее магнитное поле, создается циркулирующими в магнетике электрическими токами. Позднее электронная теория строения вещества объяснила эти токи движением электронов вокруг ядра атома.
Замкнутый ток характеризуется магнитным моментом  где I - сила тока, │
где I - сила тока, │  │ - величина площади, охватываемой контуром. Вектор
│ - величина площади, охватываемой контуром. Вектор  направлен по положительной нормали
направлен по положительной нормали  к
к  . Направление
. Направление  связано с направлением тока правилом правого винта.
связано с направлением тока правилом правого винта.
С вектором  связана индукция, которая на оси тока определяется соотношением
связана индукция, которая на оси тока определяется соотношением  , где
, где  .
.


Уравнение для напряженности
Введение вектора напряженности упрощает одно из основных уравнений магнитного поля. Упрощение уравнения для  (
( 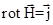 вместо
вместо 
 оправдывает его введение для описания магнитного поля в магнетиках.
оправдывает его введение для описания магнитного поля в магнетиках.
Связь между всеми величинами -  (в среде),
(в среде),  (в вакууме), характеризующими магнитное поле.
(в вакууме), характеризующими магнитное поле.
Опыт показывает, что величина магнитной поляризации │ 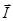 │ в некотором элементарном объеме около данной точки пропорциональна напряженности магнитного поля в магнетике в данной точке, т.е.
│ в некотором элементарном объеме около данной точки пропорциональна напряженности магнитного поля в магнетике в данной точке, т.е.
 (1)
(1)
 коэффициент, называемый магнитной восприимчивостью вещества.
коэффициент, называемый магнитной восприимчивостью вещества.
Т.к. 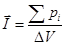 , то эта величина имеет размерность
, то эта величина имеет размерность 
Такую же размерность имеет напряженность магнитного поля (т.к.  ). Следовательно, магнитная восприимчивость - безразмерная величина.
). Следовательно, магнитная восприимчивость - безразмерная величина.
Знаете:


без магнетика  , тогда
, тогда 
Знаете два соотношения:
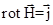 в безграничном магнетике
в безграничном магнетике
 в вакууме
в вакууме
т.е. 
т.к. 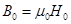 , то
, то  или
или 
Итак: 
Вывод: напряженность поля в магнетике совпадает с напряженностью внешнего поля.
Знаете:

 , то
, то

Вывод: относительная магнитная проницаемость  показывает, во сколько раз усиливается B в магнетиках
показывает, во сколько раз усиливается B в магнетиках
Диамагнетики
Особенность диамагнетиков - атомы , в отсутствие внешнего магнитного поля, не обладают отличным от 0 магнитным моментом 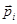 . Объяснение этого: магнитные моменты замкнутых электрических токов (или орбитальные магнитные моменты) и собственные магнитные моменты (или спиновые) сбалансированы так, что у каждого атома никакого среднего момента нет.
. Объяснение этого: магнитные моменты замкнутых электрических токов (или орбитальные магнитные моменты) и собственные магнитные моменты (или спиновые) сбалансированы так, что у каждого атома никакого среднего момента нет.
Парамагнетики
В парамагнетиках, в отсутствии внешнего поля  , магнитный момент отдельных атомов
, магнитный момент отдельных атомов  . Однако
. Однако 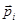 распределены хаотично, потому
распределены хаотично, потому  . Во внешнем поле,
. Во внешнем поле, 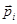 стремится ориентироваться по полю, т.к. в этом положении энергия молекул во внешнем поле минимальна
стремится ориентироваться по полю, т.к. в этом положении энергия молекул во внешнем поле минимальна  . В результате этого магнит создает свое магнитное поле
. В результате этого магнит создает свое магнитное поле  , причем
, причем  ,
,  ,
,  ,
,  .
.
Т.к.  , то
, то 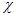 >0,
>0,  >1
>1
Расчеты для 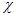 дают соотношение
дают соотношение

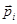 - магнитный момент одной молекулы,
- магнитный момент одной молекулы,  - концентрация молекул магнетика, к - постоянная Больцмана, T - температура, C - постоянная Кюри; при T=300К
- концентрация молекул магнетика, к - постоянная Больцмана, T - температура, C - постоянная Кюри; при T=300К  , т.е.
, т.е.  .
.
Вывод: у парамагнитных веществ диамагнитной восприимчивостью обычно можно пренебречь.
Для жидких и твердых магнетиков, у которых значительно взаимодействие между молекулами,
 ,
,
где  - характерная для данного вещества температура, определяющаяся его свойствами.
- характерная для данного вещества температура, определяющаяся его свойствами.
В разделе диамагнетизма показали: из-за того, что электрон в атоме обладает не только магнитным моментом 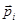 , но и электрическим, то во внешнем магнитном поле орбита электрона прецессирует вокруг
, но и электрическим, то во внешнем магнитном поле орбита электрона прецессирует вокруг  . При этом угол между
. При этом угол между 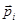 и
и  не изменяется.
не изменяется.
Переориентировка магнитных моментов в соответствии с распределением Больцмана происходит в результате столкновений и взаимодействий атомов между собой.
Ферромагнетики
Для ферромагнетиков нет простой зависимости между  и
и  , т.к.
, т.к.  .
.
Столетову удалось экспериментально получить зависимость
 ,
, 
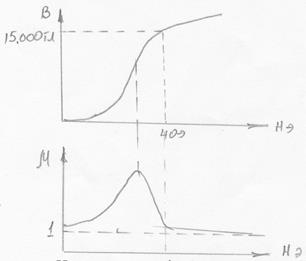
Из верхнего графика зависимости  видно:
видно:
В начале В растет медленно, потом быстрее, затем опять медленнее. В пределе функция  становится линейной. Т.к.
становится линейной. Т.к.  , то такая зависимость
, то такая зависимость  означает, что
означает, что 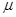 сначала быстро возрастает, потом падает и в пределе стремится к единице. Обычно
сначала быстро возрастает, потом падает и в пределе стремится к единице. Обычно 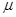 достигает максимальных значений уже в небольших полях (до одного эрстеда)
достигает максимальных значений уже в небольших полях (до одного эрстеда)
Экспериментальная зависимость  имеет вид:
имеет вид:

Видно: зависимость  тоже, с ростом H, вначале быстро возрастает, потом рост замедляется, далее величина I стремится к насыщению. Т.к.
тоже, с ростом H, вначале быстро возрастает, потом рост замедляется, далее величина I стремится к насыщению. Т.к.  , то описанная зависимость
, то описанная зависимость  означает, что
означает, что  вначале быстро возрастает, достигает максимума и, далее, уменьшается, стремясь к 0. Величина
вначале быстро возрастает, достигает максимума и, далее, уменьшается, стремясь к 0. Величина 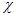 достигает максимума, при тех же полях, что и
достигает максимума, при тех же полях, что и 
Приведенные кривые носят название кривых Столетова.
Вывод: из приведенных кривых следует, что получить как угодно большие поля с помощью ферромагнетиков не удается., т.к. 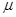 не все время растет с ростом H.
не все время растет с ростом H.
Опыт: для каждого ферромагнетика существует такая температура  (температура Кюри) , при которой его ферромагнитные свойства исчезают. При T>
(температура Кюри) , при которой его ферромагнитные свойства исчезают. При T>  ферромагнетик становится парамагнетиком. Для ферромагнетика
ферромагнетик становится парамагнетиком. Для ферромагнетика 
 . Это закон Кюри-Вейса;
. Это закон Кюри-Вейса; 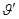 - температура Кюри-Вейса;
- температура Кюри-Вейса; 
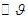 . Часто считают:
. Часто считают: 
 .
.
Антиферромагнетизм.
При определенных условиях обменное взаимодействие приводит к такой ситуации, что энергетически выгодным является анти параллельная ориентировка спинового момента соседних атомов. Для этого необходима реализация условий, аналогичных условиям возникновения ферромагнетизма, но для конфигураций с антипараллельными спинами. В результате этого спиновые магнитные моменты соседних атомов оказываются ориентированными в противоположных направлениях
Такую ситуацию можно интерпретировать как одновременное наличие двух подрешеток, которые спонтанно намагничены в противоположных направлениях с одинаковой интенсивностью. Суммарная намагниченность равна нулю. Эта ситуация называется антиферромагнетизмом, а тела, в которых она осуществляется - антиферромагнетиками.
Лекция №5
Электроемкость проводников.
Опыт  Для разных проводников
Для разных проводников  и
и 

Вывод: проводники обладают некоторым физическим свойством накапливать заряд.. его назвали емкостью. Величины  связаны зависимостью
связаны зависимостью 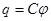
 коэффициент пропорциональности, С-емкость,
коэффициент пропорциональности, С-емкость,  т.е.
т.е.
емкость уединенного проводника есть физическая величина, численно равная количеству электричества, которое надо сообщить проводнику, чтобы потенциал его принял значение, равное единице ( т.к. при  С=q)
С=q)
Единица измерения емкости.
СГСЕ: за единицу емкости принимается емкость такого уединенного проводника, сообщение которому одной единицы СГСЕ заряда меняет ее потенциал на одну СГСЕ
единицу потенциала.
Т.к. для шара  и
и  , то С=R, т.е. в СГСЕ емкость шара численно равна его радиусу.
, то С=R, т.е. в СГСЕ емкость шара численно равна его радиусу.
Вывод: единица емкости в СГСЕ есть емкость шара радиусом 1см.
Система СИ: за единицу емкости принимается емкость такого уединенного проводника, сообщение которому заряда в 1 кулон меняет его потенциал на один Вольт. Эта единица называется фарадой.
 (в1400 раз больше радиуса земли).
(в1400 раз больше радиуса земли).
Цилиндрический конденсатор.
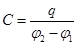 ,
, 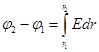 Напряженность между цилндрическими поверхностями совпадает с напряженностью от внутреннего цилиндра, т.е.
Напряженность между цилндрическими поверхностями совпадает с напряженностью от внутреннего цилиндра, т.е. 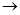
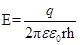 , где
, где 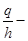 есть линейная плотность заряда
есть линейная плотность заряда 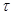 на цилиндре
на цилиндре
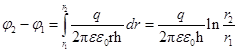 ,
, 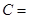
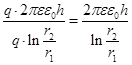
Далее желательно прочесть $ 26 "Соединение конденсаторов" Савельева (т.2 стр. 73  74)
74)
Лекция 5 (Продолжение)
Энергия электрического поля
Энергия системы неподвижных точечных зарядов. Энергия заряженного проводника, заряженного конденсатора. Объемная плотность энергии. Энергия электростатического поля.
Энергия конденсатора.
Процесс возникновения заряда на обкладках конденсатор: от одной обкладки
последовательно отнимаются малые порции  и перемещаются на другую обкладку. Работа переноса очередной порции:
и перемещаются на другую обкладку. Работа переноса очередной порции:
 где
где  -разность потенциалов между пластинами к моменту переноса на нее заряда
-разность потенциалов между пластинами к моменту переноса на нее заряда  или
или 

т.к.  =
=  , то
, то 

 и
и 

Пример №1 использования этого соотношения-определение силы взаимного притяжеия пластин плоского конденсатора
Энергия плоского конденсатора 
Выразим емкость через геометрические размеры конденсатора  (где S - площадь пластин, l-расстояние между ними). Тогда
(где S - площадь пластин, l-расстояние между ними). Тогда 
Сила F направлена по кратчайшему расстоянию между пластинами, противоположно направлению движения, тогда
 и
и 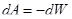 , т.е.
, т.е. 
Такое же выражение для силы А получается, если рассчитать ее по соотношению  где q-заряд одной пластины, Е-напряженность от второй пластины в месте расположения первой пластины. Знаете, что в этом случае
где q-заряд одной пластины, Е-напряженность от второй пластины в месте расположения первой пластины. Знаете, что в этом случае
 , тогда
, тогда 

Пример №2
Закон Ома
1. Основной закон постоянного тока - закон Ома. Это экспериментальный закон.

Сила тока пропорциональна разности потенциалов на концах участка проводника. Проводник однородный, если в нем нет скачков потенциалов или нет эдс
R - коэффициент пропорциональности, называется сопротивлением.
2. Единица измерения сопротивления
СГСЕ: за единицу сопротивления принимается сопротивление проводника, в котором при разности потенциалов на концах в одну СГСЕ-единицу течет одна СГСЕ единица тока.
СИ: за единицу сопротивления принимается сопротивление проводника, в котором при разности потенциалов на концах в одн вольт возникает ток в один ампер.Это - Ом.
Связь между Омом и СГСЕ единицей сопротивления:
1 Ом= 
3. R зависит от:
· материала проводника
· его размеров
· его формы
Если площадь поперечного сечения  то
то
 , где
, где  длина проводника,
длина проводника,  удельное сопротивление, равное
удельное сопротивление, равное  ,
,
т.е. удельное сопротивление численно равно сопртивлению проводника, имеющего единицу длины и единицу площади поперечного сечения
Величина  определяется химической природой вещества, температурой
определяется химической природой вещества, температурой
 =
= 
 при обычной температуре (почти для всех металлов)
при обычной температуре (почти для всех металлов)
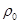 -уд. сопротивление при t=0 C
-уд. сопротивление при t=0 C
 коэффициент,
коэффициент,  .
.
При очень низких и высоких температурах это соотношение не выполняется. При температуре, равной нескольким градусам Кельвина, для большой группы металлов  скачком обращается в 0.
скачком обращается в 0.

Это явление сверхпроводимости,  температура перехода в состояние сверхпроводимости.
температура перехода в состояние сверхпроводимости.
Дифференциальная форма записи закона Ома для участка цепи.
Закон Ома  связывает величины, относящиеся к различным точкам проводника
связывает величины, относящиеся к различным точкам проводника 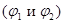 или к конечным участкам. Это закон Ома в интегральной форме.
или к конечным участкам. Это закон Ома в интегральной форме.
Дифференциальное уравнение должно связать характеристики одной точки проводника. Вокруг некоторой точки выделим элементарный цилиндрический объем.

Образующие 
Основание 


Для данного элементарного цилиндрического объема:

Направление  совпадает с направлением Е в данной точке, потому:
совпадает с направлением Е в данной точке, потому:

 плотность тока в данной точке,
плотность тока в данной точке,  напряженность поля в данной точке.
напряженность поля в данной точке.
Вывод: полученный закон Ома связывает характеристики одной точки, потому  - дифференциальная форма записи закона Ома.
- дифференциальная форма записи закона Ома.
Закон Джоуля-Ленца
Второй экспериментальный закон - закон Джоуля-Ленца

 количество тепла, выделяемого в проводнике
количество тепла, выделяемого в проводнике
 время, в течении которого выделялось тепло.
время, в течении которого выделялось тепло.
Как теоретически объяснить этот закон?

Если:
- проводник неподвижен
- не наблюдается химических реакций, то


Учтем:  т. е. совпадение с экспериментальным законом.
т. е. совпадение с экспериментальным законом.
 - интегральная форма записи закона Джоуля-Ленца.
- интегральная форма записи закона Джоуля-Ленца.
Найдем дифференциальную форму записи.
Опять вокруг т. А выделим элементарный объем - цилиндр.


 - количество теплоты, выделяющейся в единице объема в единицу времени - удельная мощность тока, тогда:
- количество теплоты, выделяющейся в единице объема в единицу времени - удельная мощность тока, тогда:
 , т.е.удельная мощность тока
, т.е.удельная мощность тока  и
и  .
.
 - дифференциальная форма записи закона Джоуля-Ленца.
- дифференциальная форма записи закона Джоуля-Ленца.
Сторонние электродвижущие силы 
Выяснили:
- перенос заряда по проводникам под действием Е сопровождается работой электрической силы
- эквивалентное этой работе количество энергии выделяется в форме джоулева тепла.
Вывод: для поддержания постоянного электрического тока необходима затрата энергии.
С другой стороны: поле постоянных токов потенциально. Следствие:  , т.е. работа электрических сил по замкнутому контуру равна 0.
, т.е. работа электрических сил по замкнутому контуру равна 0.
Вывод: в цепи постонного тока для его поддержания должна действовать сила неэлектростатического происхождения, работа которой по замкнутому контуру  и потому она может возмещать все потери энергии.
и потому она может возмещать все потери энергии.
При наличии одних кулоновских сил стационарное поле должно быть электростатическим
Т.к. положительные заряды движутся от т. с большим потенциалом к точкам с меньшим потенциалом, это приводит к выравниванию потенциалов, т.е. уничтожению причины движения.
Сила неэлектростатического происхождения, поддерживающая ток в цепи, называется сторонней силой  .
.
Можно записать выражение:

 напряженность поля сторонних сил
напряженность поля сторонних сил
Работа сторонних сил на участкет1-2:

Величина  , равная работе сторонних сил, отнесенной к единице положительного заряда, называется электродвижущей силой
, равная работе сторонних сил, отнесенной к единице положительного заряда, называется электродвижущей силой  . Обозначается
. Обозначается  буквой
буквой  .
.

Размерность  совпадает с размерностью потенциала.
совпадает с размерностью потенциала.
Если на заряд действует и электрическая сила и сторонняя, то 

Величина, численно равная работе, совершаемой электростатическими и сторонними силами при перемещении единичного положительного заряда, называется падением напряжения или просто напряжением  на данном участке пути
на данном участке пути


Закон Ома для неоднородного участка цепи
Неоднородный участок цепи - участок, на котором действует электродвижущая сила.
Если участок неоднородный, то 
Закон Ома:

 это закон Ома в дифференциальной форме для неоднородного участка.
это закон Ома в дифференциальной форме для неоднородного участка.
В интегральной форме
Возьмем участок проводника. Запишем для точки внутри него закон Ома в дифференциальной форме
 Умножим обе части равенства на
Умножим обе части равенства на 
 =
=  ;
;  ;
; 



 - закон Ома для неоднородного участка цепи в интегральной форме. Читается так: Произведение силы тока на
- закон Ома для неоднородного участка цепи в интегральной форме. Читается так: Произведение силы тока на  произвольного участка цепи равно напряжению, приложенному к заданному участку цепи.
произвольного участка цепи равно напряжению, приложенному к заданному участку цепи.
Если поле потенциально, то:

 или
или 
 - закон Ома.
- закон Ома.
Закон Ома для замкнутой цепи
Если точки 1 и 2 совпадают, т.е. 1=2, то:


Для электростатического поля  , потому
, потому

 ;
; 
 ;
; 
Сила неразветвленного постоянного тока равна частному от деления полной сторонней ЭДС в его цепи на сопротивление этой цепи.
При 

Разветвленные цепи. Правила Кирхгофа.
Обобщенный закон Ома для участка цепи

позволяет рассчитать любую сложную цепь. Однако непосредственный расчет сложных цепей довольно труден. Эта трудность в большой степени обходится, если пользоваться двумя правилами Кирхгофа, вытекающими из законов постоянного тока. Эти правила связывают силы токов, характеризующие отдельные участки цепи, их сопротивления и ЭDS, включенные в эти участки цепи.
Первое правило Кирхгофа
Оно относится к узлам цепи. Узел - это точка, в которой сходятся не меньше трех проводников цепи. Ток, текущий к узлу, считается положительным, а от узла - отрицательным.
Первое правило формулируется следующим образом: алгебраическая сумма сил токов, сходящихся в узле, равна нулю. Аналитически это записывается так:
 где
где  n - число токов, сходящихся в узле.
n - число токов, сходящихся в узле.
Обоснование этого правила
Т.к. ток в цепи постоянный, то в цепи должно оставаться неизменным распределение потенциалов между отдельными сечениями цепи. В таком случае потенциал узла остается неизменным во времени. Тогда остается неизменным и заряд узла. Но если это так, то подходящий к узлу заряд должен быть равен уходящему, потому алгебраическая сумма токов, подходящих к узлу, должна быть равна нулю.
Если в рассматриваемой системе n узлов, то независимых уравнений для токов можно составить (n-1), n-ое уравнение будет следствием (n-1) уравнений.
Второе правило Кирхгофа
В любом замкнутом контуре, произвольно выбранном в разветвленной цепи проводников, сумма произведений сил токов на сопротивление соответствующих участков цепи равна сумме ЭДС, встречающихся в этом контуре.
 где
где  число участков в замкнутом контуре, к - номер данного участка.
число участков в замкнутом контуре, к - номер данного участка.
Это правило является следствием обобщенного закона Ома для участка цепи. Покажем это на примере произвольного замкнутого контура
Обобщенный закон Ома для отдельных участков взятого контура:


Сложим левые и правые части этих равенств

 , получили правило Кирхгофа.
, получили правило Кирхгофа.
Такие уравнения можно составить для всех замкнутых контуров разветвленной цепи. Независимыми уравнениями будут только уравнения, составленные для тех контуров, которые не получаются в результате наложения уже рассмотренных. Итак: пользуясь првилами Кирхгофа, можно составить  уравнений.
уравнений.
 число узлов в разветвленной цепи
число узлов в разветвленной цепи
 число контуров, которые не получаются в результате наложения уже рассмотренных.
число контуров, которые не получаются в результате наложения уже рассмотренных.
Если число этих уравнений равно числу неизвестных, то правила Кирхгофа позволяют решить задачу.
Если число неизвестных больше, то некоторые из них не могут быть определены. Если число неизвестных меньше, то нужно составить необходимое число уравнений.
При развернутой записи уравнения второго правила Кирхгофа необходимо:
1. Выбрать определенное направление обхода замкнутого контура (например по часовой стрелке)
2. Считать положительными те токи, направление которых совпадает с направлением обхода и отрицательными те, направление которых противоположно направлению обхода
3. Считать положительными те ЭДС, которые повышают потенциал в направлении обхода. Т.к. ток течет от положительного полюса (1) к отрицательному(1), то потенциал положительного полюса выше потенциала отрицательного. Поэтому  нужно принимать положительной, если при обходе первым встречается отрицательный полюс.
нужно принимать положительной, если при обходе первым встречается отрицательный полюс.
Если не учесть верно знаки токов и ЭДС, решение окажется неверным.
Пример расчета разветвленной цепи с применением правил Кирхгофа

К одинаковых элементов с ЭДС  соединены параллельно
соединены параллельно
 внутреннее сопротивление каждого элемента
внутреннее сопротивление каждого элемента
 внешнее сопротивление, на которое замкнута батарея элементов.
внешнее сопротивление, на которое замкнута батарея элементов.
Сопротивлением соединительных проводов можно пренебречь. Определить силу тока  , протекающего по сопротивлению.
, протекающего по сопротивлению.
В данной цепи не известны величины: 
 ,
,  ,
,  ,
,  .
.
В цепи два узла. В этом случае можно составить одно независимое уравнение, допустим для узла А:
 . Токи
. Токи  ,
,  ,
,  - входят в узел, потому им приписываем знак "+". Ток
- входят в узел, потому им приписываем знак "+". Ток  выходит из узла, потому ему приписываем знак "-". тогда:
выходит из узла, потому ему приписываем знак "-". тогда:  +
+  +
+  -
-  =0. Т.к. участки А
=0. Т.к. участки А  В, А
В, А  2В и А
2В и А  абсолютно одинаковые, то
абсолютно одинаковые, то  =
=  =
=  . Тогда кi1=
. Тогда кi1= 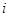
 .
.
Т.к. все четыре неизвестные величины сводятся к одной неизвестной, то достаточно составить одно уравнение по 2-у правилу Кирхгофа. С целью нахождения тока  удобно выбрать замкнутый контур
удобно выбрать замкнутый контур  . Контур будем обходить по часовой стрелке. Т.к. токи
. Контур будем обходить по часовой стрелке. Т.к. токи  1 и
1 и  противоположны направлению обхода, то берем их с отрицательными знаками, т.е.
противоположны направлению обхода, то берем их с отрицательными знаками, т.е.  .
.
При обходе по часовой стрелке ЭДС понижает потенциал, потому берем  с отрицательным знаком, т.е.
с отрицательным знаком, т.е.  . Тогда
. Тогда  т.к.
т.к.  , то
, то  ,
,  .
.
Эту формулу можно прочесть следующим образом: при параллельном соединении  одинаковых элементов в батарею, ЭДС не меняется, а внутреннее сопротивление уменьшается в
одинаковых элементов в батарею, ЭДС не меняется, а внутреннее сопротивление уменьшается в  раз.
раз.
Конец расчета индукции магнитного поля прямого тока

Из рисунка:  ;
;  Тогда:
Тогда:

Угол  меняется в пределах от
меняется в пределах от  до
до  , тогда:
, тогда:
 Итак:
Итак: 


Если проводник бесконечный по длине, то  ; . Тогда
; . Тогда
: 
 (1+1)=
(1+1)= 
Лекция 11
Магнитное поле в веществе
Намагничивание вещества. Намагниченность. Связь векторов напряженности, индукции, намагниченности. Магнитная восприимчивость, магнитная проницаемость. Ларморовская прецессия электронных орбит. Диамагнетики, парамагнетики, ферромагнетики. Магнитный гистерезис, Закон Кюри-Вейса, точка Кюри.
До сих пор рассматривали магнитное поле в пустоте, т.е. в пространстве. в котором в достаточном количестве нет атомов и элементарных частиц. Теперь рассмотрим магнитное поле в веществе. Особый интерес представляют магнетики. Это вещества, способным влиять на магнитное поле или создавать магнитное поле.
Впервые, правильное объяснение природы магнетизма выдвинул Ампер. Он предположил, что поле намагниченных магнетиков, как и внешнее магнитное поле, создается циркулирующими в магнетике электрическими токами. Позднее электронная теория строения вещества объяснила эти токи движением электронов вокруг ядра атома.
Замкнутый ток характеризуется магнитным моментом  где I - сила тока, │
где I - сила тока, │  │ - величина площади, охватываемой контуром. Вектор
│ - величина площади, охватываемой контуром. Вектор  направлен по положительной нормали
направлен по положительной нормали  к
к  . Направление
. Направление  связано с направлением тока правилом правого винта.
связано с направлением тока правилом правого винта.
С вектором  связана индукция, которая на оси тока определяется соотношением
связана индукция, которая на оси тока определяется соотношением  , где
, где  .
.


Дата: 2018-11-18, просмотров: 703.