Поле намагниченных магнетиков создается не только магнитными моментами замкнутых электронных токов, но и магнитными моментами самих электронов. Квантовая механка показала, что все элементарные частицы обладают собственными магнитными и механическими моментами. В различных магнетиках роль магнитных моментов токов электронов и собственных магнитных моментов различна.

В отсутствие внешнего магнитного поля магнитные моменты отдельных атомов равны 0, либо ориентированы в пространстве хаотически. Когда магнетик попадает во внешнее магнитное поле, магнитные моменты стремятся ориентироваться вдоль индукции 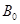 этого поля. Ориентированные магнитные моменты создают свое магнитное поле, индукцию которого обозначим 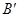. Магнетик, находящийся в таком состоянии, называется намагниченным. Для характеристики меры намагниченности магнетика вводится вектор магнитной поляризации (поляризуемость) .

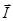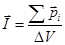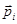где  - магнитный момент i-го атома, V - объем магнетика, суммирование проводится по всем атомам, т.е. 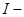магнитный момент, приходящийся на единичный объем магнетика.

Сказали: возникновение магнитных моментов связано с наличием круговых токов. Эти токи называются молекулярными. При определении намагниченности подразумеваются

усредненные величины. Магнитные моменты молекул представляются размазанными по

всему объему, а молекулярные токи - текущими по объему магнетика, как в непрерывной среде.

Найдем связь между вектором намагничивания 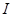с молекулярным токами, создающими магнитные моменты.

Связь 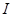 с объемными токами.

 Рассмотрим бесконечно малый замкнутый контур L, ограничивающий 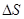 и вычислим циркуляцию намагниченности I (или вектора магнитной индукции) по контуру:

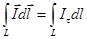    (1)

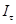 - тангенциальная составляющая I вдоль контура интегрировния

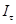 создается за счет токов, текущих по замкнутым контурам вокруг линии, вдоль которой производится интегрирование

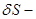площадь, обтекаемая током в плоскости, перпендикулярной линии интегрирования

Умножив числитель и знаменатель (1) на 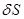, проведем следующие преобразования:

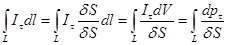
По определению магнитного момента 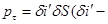сила молекулярного тока, обтекающего площадку  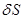по длине dl, причем  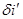пересекает  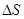по нормали). Поэтому:

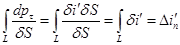
где нормальная составляющая силы тока, пересекающего площадку .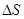

Таким образом:

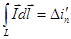            (2)

1. Запишем ток, пересекающий площадку 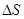 через плотность тока
2. Применим к левой части равенства (2) теорему Стокса

Тогда: 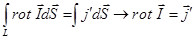                     (3)

Эта формула - связь намагниченности с объемной плотностью молекулярных токов, создающих эту намагниченность.

Если однородный магнетик находится в однородном внешнем магнитном поле, то объемных молекулярных токов, создающих намагниченность, нет.

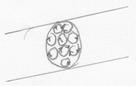
Возьмем поперечное (произвольное) сечение стержня из магнетика.

В каждой точке внутри стержня смежные молекулярные токи текут в противоположные стороны, так что их совместный ток равен нулю. Не скомпенсированными будут лишь участки токов, примыкающих к поверхности стержня

Вывод: суммарное действие молекулярных токов будет таким, какое вызвал бы макроскопический ток, текущий по поверхности стержня.

Найдем в этом случае связь между намагниченностью I и поверхностным током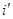

На рисунке - граница раздела двух магнетиков - 1 и 2.

Проведем в плоскости, перпендикулярной границе раздела, контур L. Параллельные границе раздела части контура равны 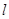, а перпендикулярные стремятся к 0. Площадь, ограниченная контуром L, - S, dS - элемент этой площади.

Умножая обе части равенства (3) на 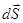 и интегрируя по S, находим

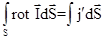                (4)

Левую часть преобразуем по т. Стокса:

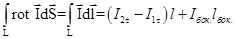
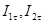 - тангенциальные к контуру интегрирования составляющие в 1-ой и 2-ой средах, знак "-" у  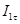появился из-за изменения направления интегрирования на обратное во 2-ой среде.

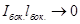, т.к.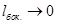

Правая часть уравнения (4): 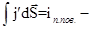проекция тока по направлению нормали к поверхности S. Этот ток - поверхностный. Он тангенциален поверхности раздела магнетиков. Окончательно соотношение (4) принимает вид:

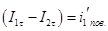                         (5)

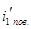 - молекулярный поверхностный ток, приходящийся на единицу длины среды.

Можно показать, что формула (5) справедлива при произвольной ориентировке контура относительно различных направлений вдоль поверхности раздела, направленный во вторую среду.

Если одной из сред является вакуум, то I₂=0 и , соответственно,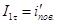

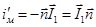               (6)