Атом с движущимися электронами - гироскоп, обладающий магнитным моментом
Момент импульса электрона 
Движущийся электрон эквивалентен току 
Тогда магнитный момент атома 
Итак:  ;
;  ;
;  <0, потому
<0, потому  . Тогда:
. Тогда: 
Уравнение движения атома, рассматриваемого как гироскоп:
 ;
;  ,
, 
 (9)
(9)
Сравним (9) с уравнением движения точек абсолютно твердого тела, вращающегося с угловой скоростью 
 показывает, что конец вектора
показывает, что конец вектора  движется вокруг направления вектора индукции с частотой
движется вокруг направления вектора индукции с частотой

Вывод: атом совершает в магнитном поле, подобно гироскопу, прецессионное движение. Оно называется Ларморовой прецессией.
Т.к.  <0, то
<0, то  .
.
Прецессия электрона эквивалентна замкнутому току. Направление этого тока противоположно направлению движения электронов. Поэтому направление тока образует левовинтовую систему с  и с
и с  . Этот ток
. Этот ток  создает свое магнитное поле
создает свое магнитное поле  , направление которого составляет с током правовинтовую систему.
, направление которого составляет с током правовинтовую систему.


Вывод: под действием внешнего поля магнетик создает свое поле, индукция которого противоположна индукции внешнего поля.
Вектор магнитной поляризации этого поля  тоже направлен противоположно
тоже направлен противоположно  , т.к.
, т.к.

 образует с направлением
образует с направлением  правовинтовую систему
правовинтовую систему
Итак:  ;
;  (т.к.
(т.к.  )
)
т.к.  , то
, то 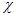 <0. Т.к.
<0. Т.к. 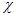 <0, то
<0, то  <1.
<1.
Расчет показывает (см. Матвеев "Электричество и магнетизм" 1983 г. стр. 291), что для диамагнетиков 

 , <
, <  > - средний квадрат расстояния электронов от ядра в атоме, N - концентрация атомов, z - число электронов в атоме
> - средний квадрат расстояния электронов от ядра в атоме, N - концентрация атомов, z - число электронов в атоме
 не зависит от температуры.
не зависит от температуры.
В отсутствие внешнего магнитного поля уравнение движения электрона в атоме:
 где
где  - сила притяжения электрона ядром.
- сила притяжения электрона ядром.
Сила  весьма велика по сравнению с силами, которые могут действовать на электрон со стороны внешних полей. Поэтому радиусы орбит электронов , при помещении атома во внешнее поле, не изменяются.Атом, в отношении действия внешних полей, можно считать жестким.
весьма велика по сравнению с силами, которые могут действовать на электрон со стороны внешних полей. Поэтому радиусы орбит электронов , при помещении атома во внешнее поле, не изменяются.Атом, в отношении действия внешних полей, можно считать жестким.
Поскольку скорость электрона в атоме, помещенном в магнитное поле, изменяется, то изменяется и его кинетическая энергия. С другой стороны, поскольку r остается неизменным, потенциальная энергия не изменяется.Это можно объяснить так: при возникновении магнитного поля порождается электрическое поле, под действием которого изменяется скорость движения электронов в атоме.
Парамагнетики
В парамагнетиках, в отсутствии внешнего поля  , магнитный момент отдельных атомов
, магнитный момент отдельных атомов  . Однако
. Однако 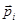 распределены хаотично, потому
распределены хаотично, потому  . Во внешнем поле,
. Во внешнем поле, 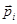 стремится ориентироваться по полю, т.к. в этом положении энергия молекул во внешнем поле минимальна
стремится ориентироваться по полю, т.к. в этом положении энергия молекул во внешнем поле минимальна  . В результате этого магнит создает свое магнитное поле
. В результате этого магнит создает свое магнитное поле  , причем
, причем  ,
,  ,
,  ,
,  .
.
Т.к.  , то
, то 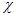 >0,
>0,  >1
>1
Расчеты для 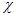 дают соотношение
дают соотношение

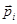 - магнитный момент одной молекулы,
- магнитный момент одной молекулы,  - концентрация молекул магнетика, к - постоянная Больцмана, T - температура, C - постоянная Кюри; при T=300К
- концентрация молекул магнетика, к - постоянная Больцмана, T - температура, C - постоянная Кюри; при T=300К  , т.е.
, т.е.  .
.
Вывод: у парамагнитных веществ диамагнитной восприимчивостью обычно можно пренебречь.
Для жидких и твердых магнетиков, у которых значительно взаимодействие между молекулами,
 ,
,
где  - характерная для данного вещества температура, определяющаяся его свойствами.
- характерная для данного вещества температура, определяющаяся его свойствами.
В разделе диамагнетизма показали: из-за того, что электрон в атоме обладает не только магнитным моментом 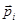 , но и электрическим, то во внешнем магнитном поле орбита электрона прецессирует вокруг
, но и электрическим, то во внешнем магнитном поле орбита электрона прецессирует вокруг  . При этом угол между
. При этом угол между 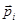 и
и  не изменяется.
не изменяется.
Переориентировка магнитных моментов в соответствии с распределением Больцмана происходит в результате столкновений и взаимодействий атомов между собой.
Ферромагнетики
Для ферромагнетиков нет простой зависимости между  и
и  , т.к.
, т.к.  .
.
Столетову удалось экспериментально получить зависимость
 ,
, 
Из верхнего графика зависимости  видно:
видно:
В начале В растет медленно, потом быстрее, затем опять медленнее. В пределе функция  становится линейной. Т.к.
становится линейной. Т.к.  , то такая зависимость
, то такая зависимость  означает, что
означает, что  сначала быстро возрастает, потом падает и в пределе стремится к единице. Обычно
сначала быстро возрастает, потом падает и в пределе стремится к единице. Обычно  достигает максимальных значений уже в небольших полях (до одного эрстеда)
достигает максимальных значений уже в небольших полях (до одного эрстеда)
Экспериментальная зависимость  имеет вид:
имеет вид:

Видно: зависимость  тоже, с ростом H, вначале быстро возрастает, потом рост замедляется, далее величина I стремится к насыщению. Т.к.
тоже, с ростом H, вначале быстро возрастает, потом рост замедляется, далее величина I стремится к насыщению. Т.к.  , то описанная зависимость
, то описанная зависимость  означает, что
означает, что  вначале быстро возрастает, достигает максимума и, далее, уменьшается, стремясь к 0. Величина
вначале быстро возрастает, достигает максимума и, далее, уменьшается, стремясь к 0. Величина 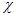 достигает максимума, при тех же полях, что и
достигает максимума, при тех же полях, что и 
Приведенные кривые носят название кривых Столетова.
Вывод: из приведенных кривых следует, что получить как угодно большие поля с помощью ферромагнетиков не удается., т.к. 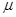 не все время растет с ростом H.
не все время растет с ростом H.
Опыт: для каждого ферромагнетика существует такая температура  (температура Кюри) , при которой его ферромагнитные свойства исчезают. При T>
(температура Кюри) , при которой его ферромагнитные свойства исчезают. При T>  ферромагнетик становится парамагнетиком. Для ферромагнетика
ферромагнетик становится парамагнетиком. Для ферромагнетика 
 . Это закон Кюри-Вейса;
. Это закон Кюри-Вейса; 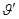 - температура Кюри-Вейса;
- температура Кюри-Вейса; 
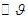 . Часто считают:
. Часто считают: 
 .
.
Дата: 2018-11-18, просмотров: 726.