1. Геометрический смысл знака трехчлена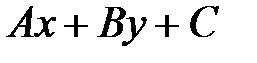 
.
Теорема 1. Если в аффинной системе координат прямая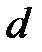 
задана уравнением 
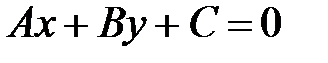, то полуплоскости с границей 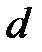определяются неравенствами 
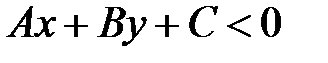и 
.
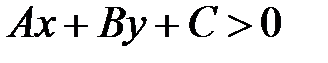Сформулированная теорема, выражающая геометрический смысл знака трехчлена 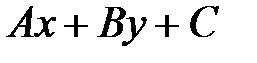, позволяет выяснять, лежат ли две точки по одну сторону от прямой 
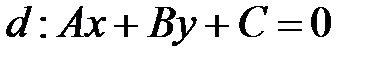или по разные стороны. Рассмотрим простейший пример.
Задача 1. Выяснить, пересекает ли прямая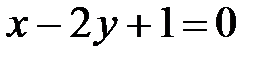 
отрезок 
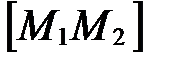, если 
.
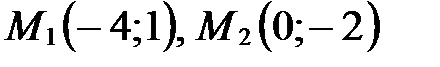Решение. Определим знак трехчлена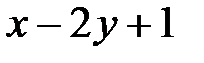 
в точке 
.
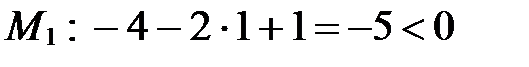Определим знак трехчлена 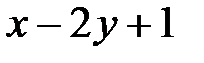в точке 
.
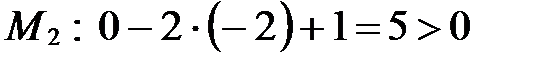Следовательно, точк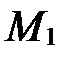и 
и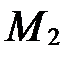 
лежат по разные стороны от данной прямой, поэтому прямая 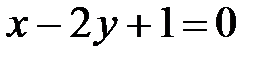пересекает отрезок .
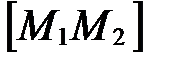Выяснение расположения точек относительно прямой, в свою очередь, применяется при решении геометрических задач, связанных с нахождением условий, определяющих внутренние области углов, треугольников или полос.
2. Взаимное расположение двух прямых.
Теорема 2. Пусть в аффинной системе координат прямая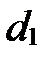 
задана уравнением 
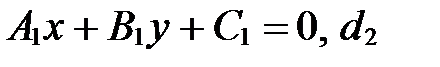- уравнением 
.
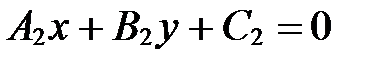1) Прямые 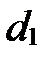и 
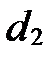пересекаются тогда и только тогда, когда коэффициенты пр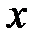и 
и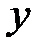 
в их уравнениях не пропорциональны, т.е.
;
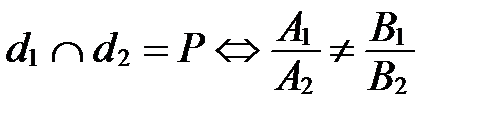Чтобы найти координаты точки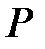 
пересечения прямых 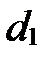и 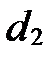, надо решить систему уравнени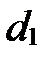й и .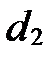
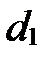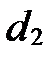2) Прямые и параллельны тогда и только тогда, когда коэффициенты пр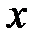и и 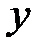пропорциональны, а свободные члены им не пропорциональны, т.е.
;
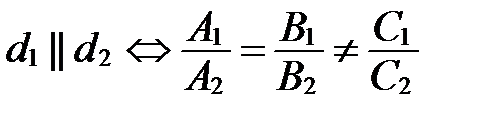3) Прямые 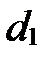и 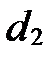совпадают тогда и только тогда, когда коэффициенты пр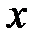и и 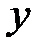и свободные члены в их уравнениях пропорциональны, т.е.
.
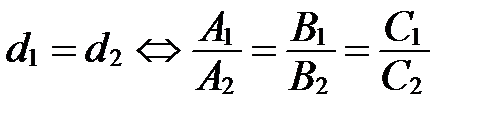Рассмотрим пример применения этой теоремы.
Задача 2. Выяснить взаимное расположение прямых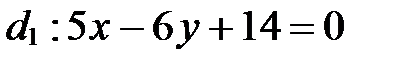 
и 
.
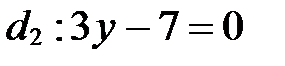Решение. Находим из уравнений прямых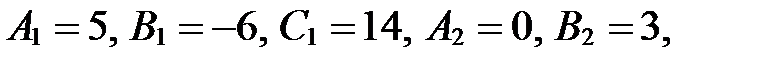 
.
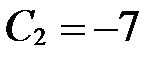Отношение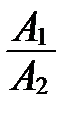 
мы найти не можем, т.к. делить на 0 нельзя. Поэтому поменяем прямые местами и найдем отношения
.
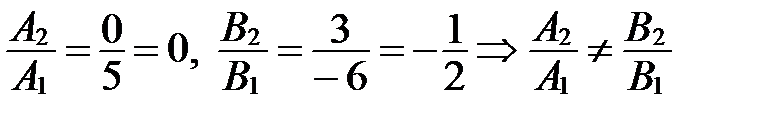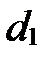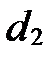Следовательно, прямые и пересекаются. Отношение 
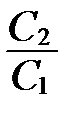находить уже нет необходимости.
Задача 3. Найти уравнение прямой, проходящей через точку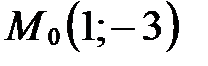 
и параллельной прямой 
.
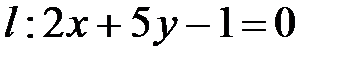Решение. Пусть 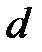- искомая прямая.
Заметим, что задачу можно решить разными способами. Например, взяв за направляющий вектор прямой 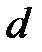направляющий вектор 
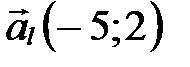прямой 
(т.к. 
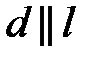, то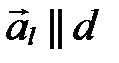 
), можно воспользоваться каноническим уравнением прямой .
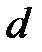Но мы решим задачу, используя теорему 2.
Из теоремы 2 следует, что так как 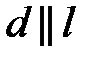, то общее уравнение прямой 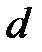будет иметь вид:
,
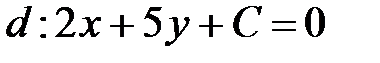т.е. можно считать, что отличаться уравнения прямых 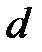и будут только свободными членами.
Чтобы найти С, используем то, что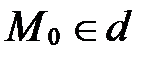 
. Подставляя координаты точки 
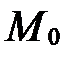в уравнение прямой 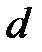, найдем С: 
.
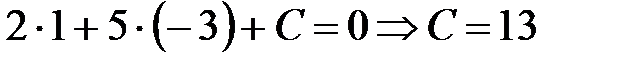Тогда
.
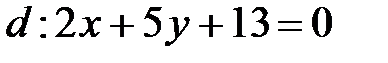3. Пучок прямых. Уравнение пучка прямых.
Множество всех прямых плоскости, проходящих через данную точку 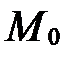, называется пучком прямых. Точка 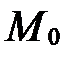называется центром этого пучка.
Множество всех прямых плоскости, параллельных данной прямой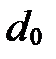 
, называется пучком параллельных прямых.
Пучок прямых определяется заданием его центра 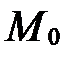, пучок параллельных прямых – заданием ненулевого вектора 
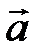, параллельного прямым пучка.
Теорема 3. Пусть известны в аффинной системе координат уравнения двух прямых пучка с центром в точке :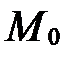
,
.
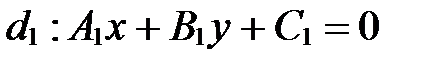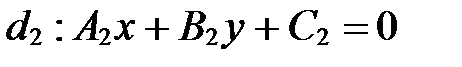Тогда уравнение пучка прямых с центром 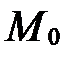будет иметь вид:
,
|
|
|
|
|
|
|
|
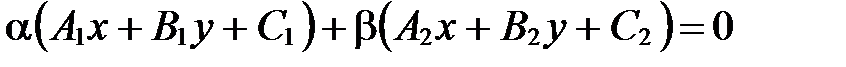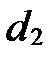
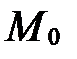
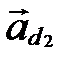
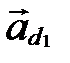
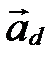
| Рис. 60 |
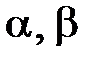- действительные числа, не равные нулю одновременно. Они определяют некоторую прямую 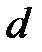пучка.
Геометрический смысл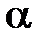 
и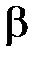 
: это координаты направляющего вектора 
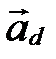прямой 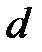в базисе 
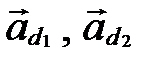(рис. 60).
Рассмотрим пример применения этой теоремы.
Задача 4. Найти уравнение прямой 
, проходящей через точку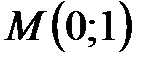 
и через точку пересечения прямых 
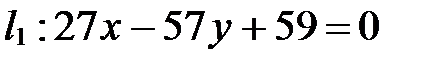и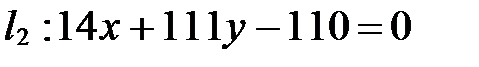 
.
Решение. Заметим, что искомое уравнение можно найти, вычислив координаты точки 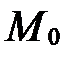пересечения прямых 
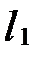и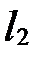 
и применив уравнение прямой, заданной двумя точками. Но при решении системы уравнений прямых 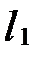и 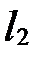получаются громоздкие вычисления.
Поэтому задачу лучше решить по теореме 3. Запишем уравнение пучка прямых с центром в точке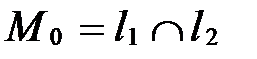 
:
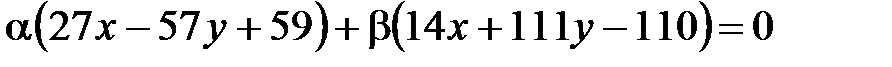, (18)
где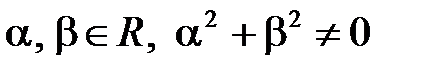 
.
Так как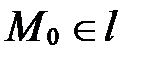 
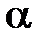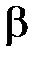, то искомая прямая принадлежит данному пучку. Найдем и , определяющие . Так как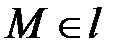 
, то ее координаты удовлетворяют уравнению (18):
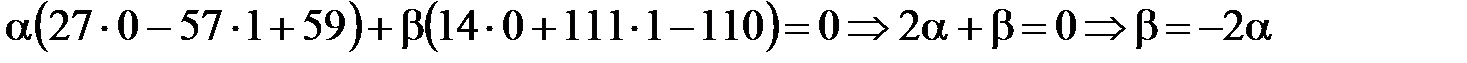. Подставим 
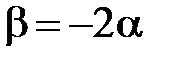в уравнение (18): 
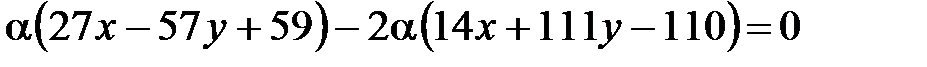. Заметим, что 
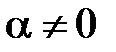(действительно, если 
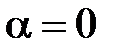, то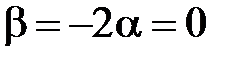 
- противоречие с условием 
).
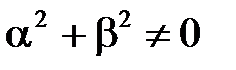Разделим обе части уравнения на :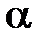
; 
.
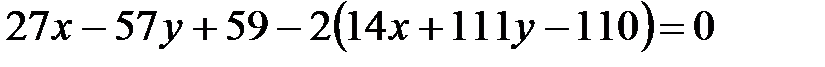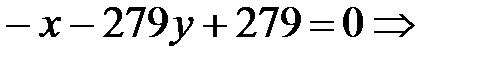
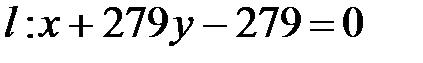Лекция 10
Дата: 2018-11-18, просмотров: 353.
