И их свойства
Множество всех векторов, на котором введена операция сложения векторов, удовлетворяющая свойствам
10. 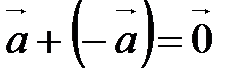 ;
;
20. 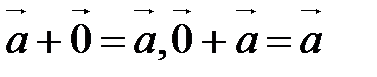 ;
;
30. 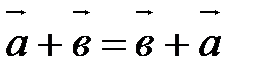 ;
;
40. 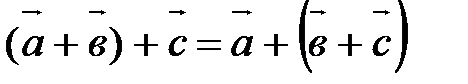 ,
,
и операция умножения вектора на число, удовлетворяющая свойствам
10. 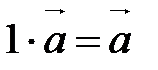 ,
, 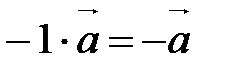 ;
;
20. 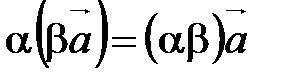 ;
;
30. 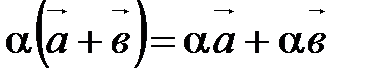 ;
;
40. 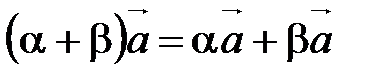 ,
,
называется векторным пространством и обозначается через V.
Базисом векторного пространства называется система векторов, заданных в определенном порядке, которая удовлетворяет условиям:
1) система линейно независима;
2) любой вектор пространства является линейной комбинацией данной системы векторов.
Число векторов базиса называется размерностью векторного пространства.
Выяснить, чему равна размерность векторного пространства V, позволяют следующие две теоремы, которые приведем без доказательства:
Теорема 1. Любая система трех некомпланарных векторов, взятых в определенном порядке, образует базис векторного пространства.
А может ли базис пространства V состоять меньше, чем из трех векторов? Больше, чем из трех векторов? Оказывается, нет, так как справедлива
Теорема 2. Любой базис векторного пространства V состоит из трех векторов.
Эти теоремы можно доказать, пользуясь теоремами о коллинеарных и компланарных векторах и свойствами 20 - 70 линейно зависимой системы векторов.
Из теорем 1 и 2 следует, что размерность векторного пространства V равна 3, поэтому оно называется трехмерным векторным пространством.
Базис, состоящий из векторов 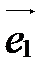 ,
, 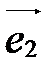 и
и 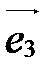 , обозначается так:
, обозначается так: 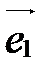 ,
, 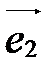 ,
, 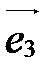 или
или 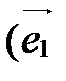 ,
, 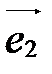 ,
, 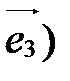 . Векторы
. Векторы 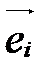 ,
, 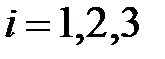 , называются базисными векторами:
, называются базисными векторами: 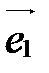 - первый базисный вектор,
- первый базисный вектор, 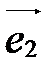 - второй,
- второй, 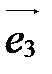 - третий.
- третий.
Пусть 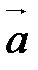 - произвольный вектор пространства V,
- произвольный вектор пространства V, 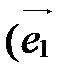 ,
, 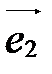 ,
, 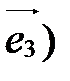 - базис векторного пространства V.
- базис векторного пространства V.
Из теоремы 1 следует, что вектор 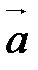 можно разложить по базисным векторам
можно разложить по базисным векторам 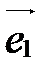 ,
, 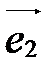 ,
, 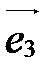 , т.е. существуют такие действительные числа
, т.е. существуют такие действительные числа 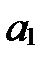 ,
, 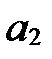 ,
, 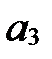 , что
, что
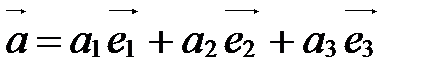 .
.
Коэффициенты 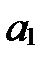 ,
, 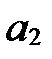 ,
, 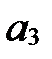 в этом разложении называются координатами вектора
в этом разложении называются координатами вектора 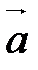 в базисе
в базисе 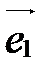 ,
, 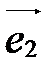 ,
, 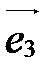 :
: 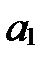 - первая координата,
- первая координата, 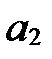 - вторая,
- вторая, 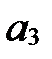 - третья.
- третья.
Обозначают это так: 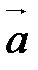 (
( 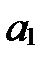 ;
; 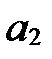 ;
; 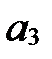 )
) 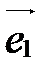 ,
, 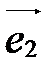 ,
, 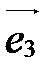 .
.
Когда ясно, о каком базисе идет речь, пишут так: 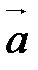 (
( 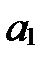 ;
; 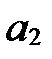 ;
; 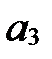 ).
).
Свойства координат векторов
10. Нулевой вектор в любом базисе имеет нулевые координаты: 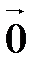 (0;0;0).
(0;0;0).
□ Разложим 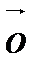 по векторам базиса
по векторам базиса 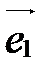 ,
, 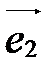 ,
, 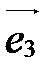 :
:
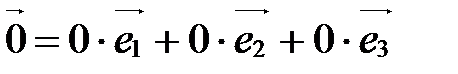 .
.
Следовательно, 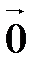 (0;0;0)
(0;0;0) 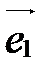 ,
, 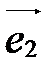 ,
, 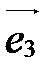 . ■
. ■
20. Если 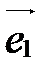 ,
, 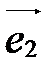 ,
, 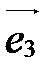 - базис пространства V, то
- базис пространства V, то 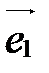 (1;0;0),
(1;0;0), 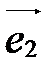 (0;1;0),
(0;1;0), 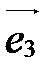 (0;0;1).
(0;0;1).
□ 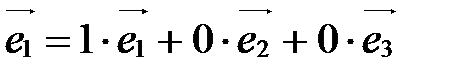
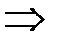
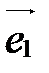 (1;0;0);
(1;0;0);
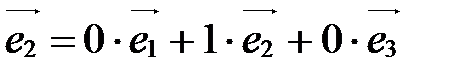
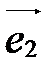 (0;1;0);
(0;1;0);
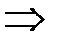
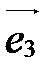 (0;0;1). ■
(0;0;1). ■
30. Если 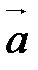 (
( 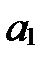 ;
; 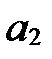 ;
; 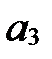 ),
), 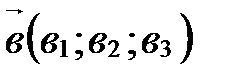 в базисе
в базисе 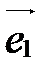 ,
, 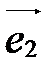 ,
, 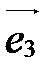 , а
, а 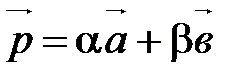 , то
, то
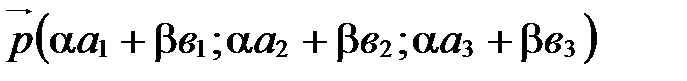
в базисе 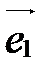 ,
, 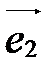 ,
, 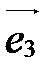 (координаты линейной комбинации векторов равны линейным комбинациям их соответствующих координат).
(координаты линейной комбинации векторов равны линейным комбинациям их соответствующих координат).
□ По определению координат вектора
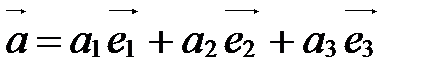 ,
, 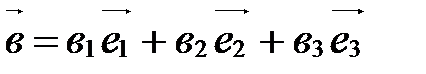 .
.
Тогда 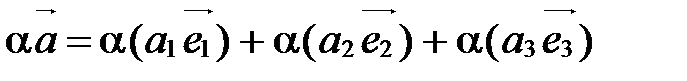 ,
, 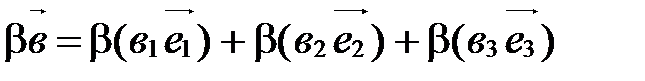 .
.
Сложим почленно эти равенства и воспользуемся свойствами сложения векторов и умножения вектора на число:
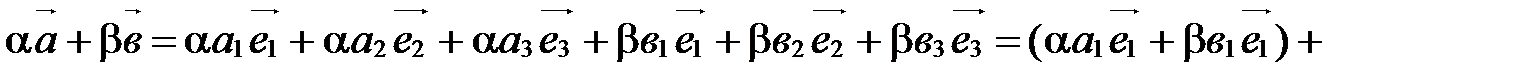
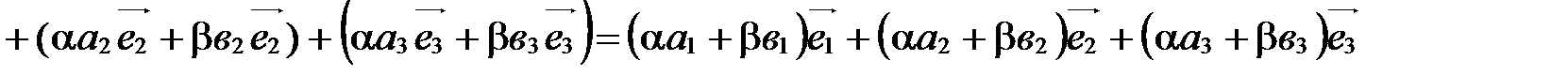 .
.
По определению координат вектора
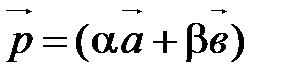
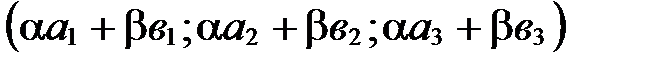 . ■
. ■
Из свойства 30 получаем следствия:
Следствие 1. Каждая координата суммы (разности) двух векторов равна сумме (разности) соответствующих координат этих векторов.
Следствие 2. При умножении вектора на число каждая его координата умножается на это число.
□ Чтобы доказать справедливость следствия 1, надо в свойстве 30 взять сначала a=b=1, а затем a=1, b=-1. Для доказательства следствия 2 полагаем b=0. ■
40. Векторы равны тогда и только тогда, когда равны их соответствующие координаты: 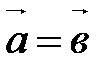

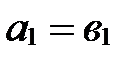 ,
, 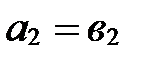 ,
, 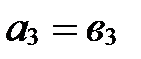 .
.
50. Пусть 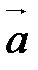 (
( 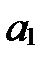 ;
; 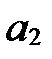 ;
; 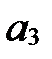 ),
), 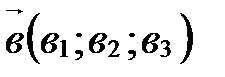 ,
, 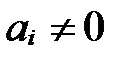 и
и 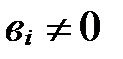 , i =1, 2, 3. Векторы
, i =1, 2, 3. Векторы 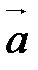 и
и 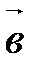 коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны:
коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны:
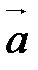 ||
|| 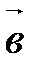

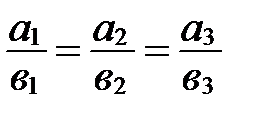 .
.
Пусть 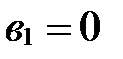 . Тогда
. Тогда
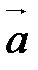 ||
|| 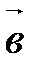

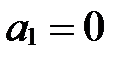 и
и 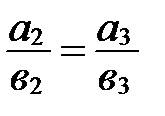 .
.
Если же 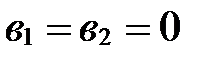 , то
, то
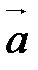 ||
|| 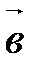

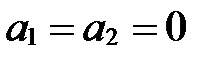 , а
, а 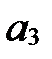 и
и 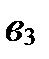 - любые.
- любые.
Частным случаем произвольного базиса является ортонормированный базис. Его удобно использовать при решении метрических задач (т.е. задач, связанных с вычислением длин отрезков (векторов) и величин углов).
| Е1 |
| Е3 |
| О |
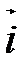
|
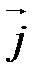
|
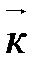
|
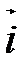 ,
, 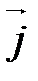 ,
, 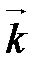 называется ортонормированным, если его векторы удовлетворяют двум условиям:
называется ортонормированным, если его векторы удовлетворяют двум условиям:
1) 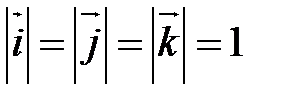 ;
;
| Рис. 8 |
| Е2 |
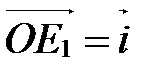 ,
, 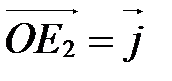 ,
, 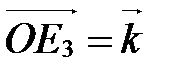 (рис. 8), то углы
(рис. 8), то углы 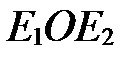 ,
, 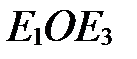 и
и 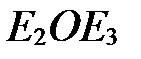 - прямые.
- прямые.
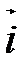
|
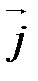
|
| Рис. 9 |
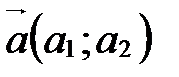 . Ортонормированный базис выглядит так:
. Ортонормированный базис выглядит так: 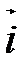 ,
, 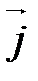 (рис. 9).
(рис. 9).
Нелинейные операции над векторами
Дата: 2018-11-18, просмотров: 400.