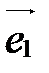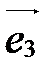Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Пусть , ,  - базис трехмерного векторного пространства.

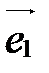
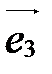
Рис. 16

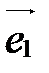
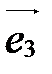
Рис. 17

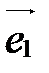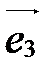Базис , ,  называется правым (левым), если при взгляде на плоскость векторов  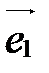и  из конца третьего вектора 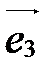 кратчайший поворот от первого вектора  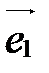ко второму вектору  виден как идущий против часовой стрелки (по часовой стрелке). На рис. 16 изображен правый базис, на рис. 17 – левый.

  

 

Можно дать и другие определения правого и левого базиса, например, такое: базис 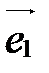, ,  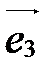называется правым (левым), если эти векторы, отложенные от одной точки, располагаются так же, как расставлены (примерно под прямым углом) пальцы правой (левой) руки: большой палец – по первому вектору 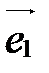, указательный – по , средний – по .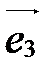

Мы будем пользоваться в дальнейшем первым определением.

Если два базиса правые (или левые), то говорят, что они одинаково ориентированы или имеют одинаковую ориентацию. Если один базис правый, а другой – левый, то говорят, что они противоположно ориентированы или имеют противоположную ориентацию.

Множество всех правых (всех левых) базисов в пространстве V называется правой (левой) ориентацией векторного пространства V.

Таким образом, в векторном пространстве ориентацию можно задать двумя способами: правую и левую. Векторное пространство, в котором выбрана ориентация, называется ориентированным. Как только в пространстве мы зададим базис, так сразу оно становится ориентированным.

В дальнейшем, если нет специальных оговорок, когда в пространстве выбран базис, будем считать, что он является правым.

Аналогично можно ввести понятие ориентированной плоскости. При этом базис 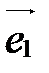,  на плоскости называется правым (левым), если кратчайший поворот от первого базисного вектора 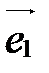 ко второму осуществляется против часовой стрелки (по часовой стрелке).

 

Векторное произведение двух векторов

Пусть 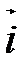, , 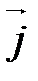 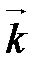- ортонормированный базис трехмерного векторного пространства V (правый). Векторным произведением двух неколлинеарных векторов  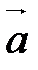и 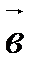 называется вектор, обозначаемый  (или 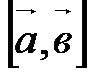) и удовлетворяющий трем условиям:

1) длина ;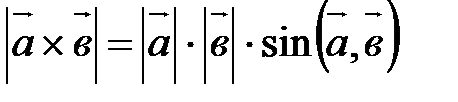

2) 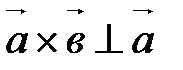 и ;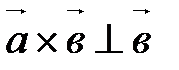

3) базис 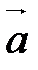, , 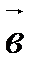 ориентирован так же, как базис , , .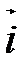

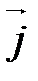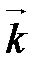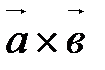
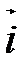
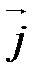
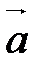
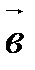
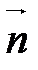
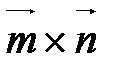
Рис. 20

Векторным произведением двух коллинеарных векторов называется нулевой вектор.

 

 

На рис. 20 изображены векторные произведения 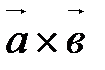 и .

Геометрические свойства

Векторного умножения векторов

Г1⁰. || .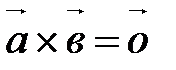

Пусть 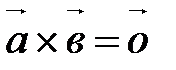, тогда

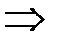
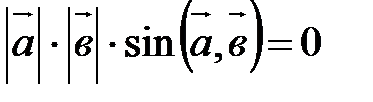
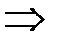
или || ;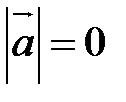

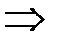
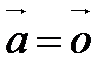
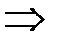
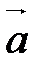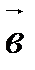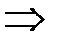  или || || ;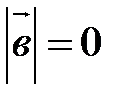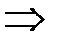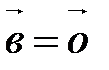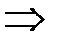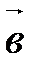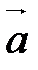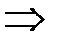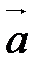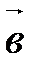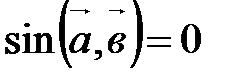

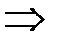
или  или || .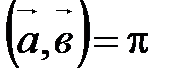

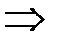
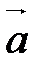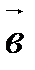Пусть 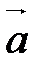|| 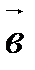. Тогда по определению векторного произведения .

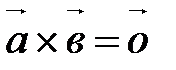А

В

D

C

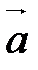
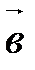
Рис. 21

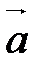Г2⁰. Длина  векторного произведения векторов  и 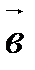 равна площади параллелограмма, построенного на этих векторах.

По определению 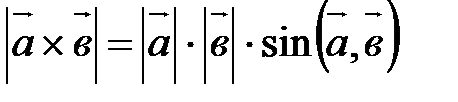. С другой стороны,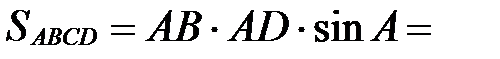

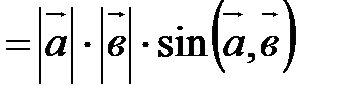 (рис. 21).

Следовательно, .

Алгебраические свойства