1⁰. Система, состоящая из одного вектора, линейно зависима тогда и только тогда, когда этот вектор нулевой.

□ Пусть система, состоящая из одного вектора 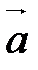, линейно зависима. Докажем, что вектор .

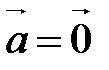Из определения линейно зависимой системы следует, что существует 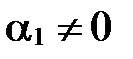 такое, что 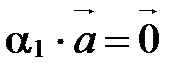. Так как первый сомножитель в левой части не равен 0, то второй сомножитель должен быть нулевым вектором, т.е. .

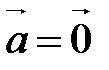Пусть, обратно, 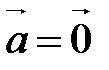. Докажем, что система, состоящая из одного вектора 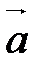, линейно зависима. Левую часть равенства можно записать в виде 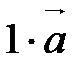, следовательно, 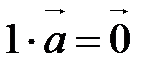, т.е. существует  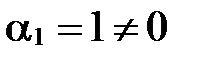такое, что 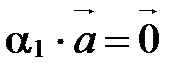. По определению линейно зависимой системы векторов система  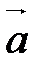линейно зависима. ■

2⁰. При n>1 система векторов 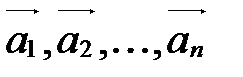 линейно зависима тогда и только тогда, когда хотя бы один из них является линейной комбинацией остальных векторов этой системы.

□ Пусть система векторов 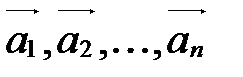 линейно зависима. Докажем, что один из ее векторов является линейной комбинацией остальных векторов этой системы.

По определению линейно зависимой системы векторов существуют числа 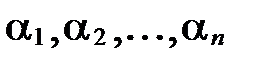, не все равные 0 одновременно, такие, что

.

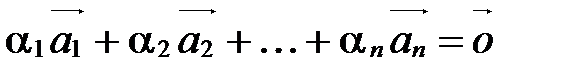Пусть для определенности 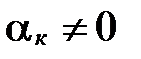, где к – одно из чисел 1, 2, ..., n. Перенесем все слагаемые, кроме 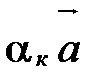, из левой части равенства в правую и разделим обе части равенства на :

.

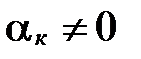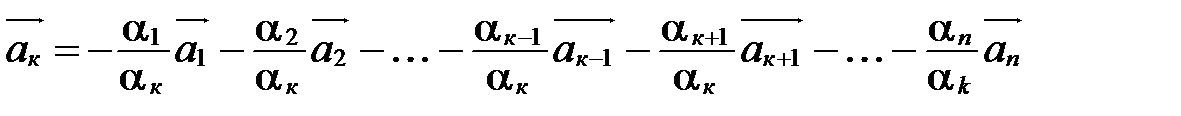Следовательно, вектор 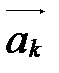 есть линейная комбинация векторов .

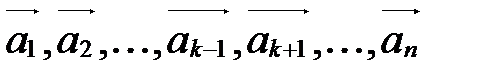Пусть теперь один из векторов системы 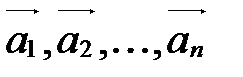, например, 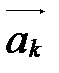, является линейной комбинацией векторов 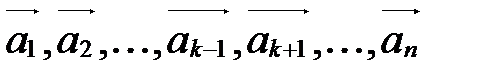. Докажем, что система векторов  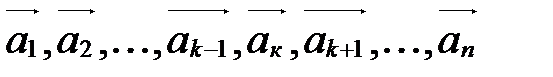линейно зависима.

По условию 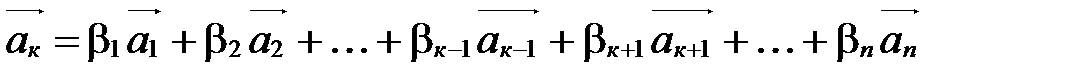. Перенесем  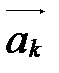в правую часть и поставим это слагаемое между  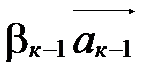и :

.

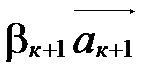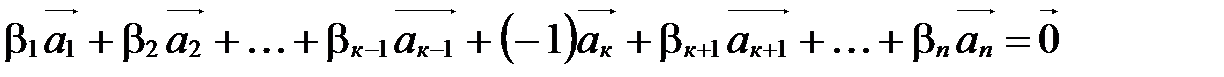Таким образом, существуют такие числа 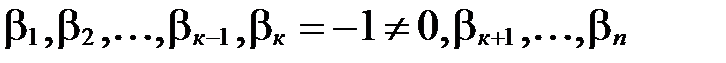, не все равные 0 одновременно, что выполняется векторное равенство

.

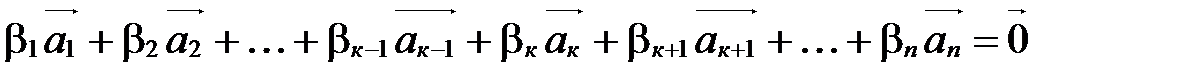Следовательно, система векторов 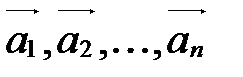 линейно зависима. ■

3⁰. Если часть данной системы векторов линейно зависима, то и вся система линейно зависима.

□ Пусть дана система векторов 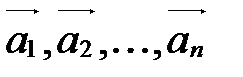 и известно, что ее подсистема 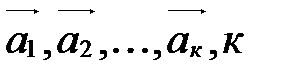<n, линейно зависима. Тогда существуют такие числа 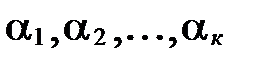, причем 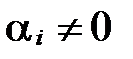, что .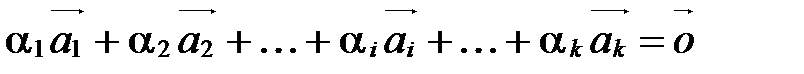

Тогда ,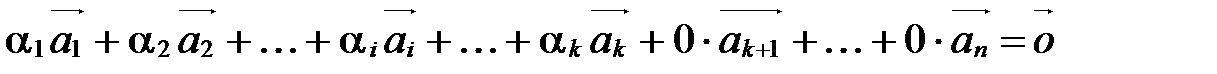

т.е. нашлись числа 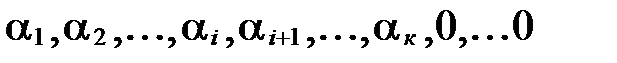, причем 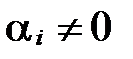, следовательно, система  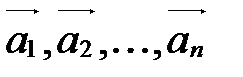линейно зависима. ■

4⁰. Система линейно независимых векторов не содержит нулевого вектора.

□ Пусть система 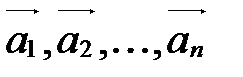 линейно независима. Предположим, что она содержит 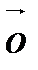. По свойству 1⁰ система  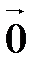линейно зависима. Тогда по свойству 3⁰ вся система  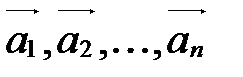линейно зависима. Получили противоречие с условием. ■

5⁰. Если система векторов линейно независима, то любая ее часть линейно независима.

 □ Предположим, что существует часть данной системы, являющаяся линейно зависимой. Тогда по свойству 3⁰ вся данная система должна быть линейно зависимой. Получили противоречие с условием. ■

6⁰. Система векторов 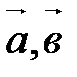 линейно зависима тогда и только тогда, когда || .

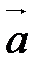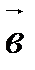□ Пусть система векторов 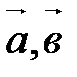 линейно зависима. Тогда по свойству 2⁰ 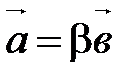или , или 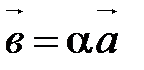. По теореме о коллинеарных векторах || .

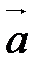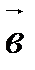Пусть 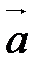|| 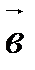. Если один из векторов нулевой, например, 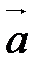, то по свойству 4⁰ система 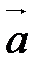,  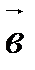линейно зависима. Если 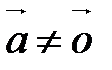, то по теореме о коллинеарных векторах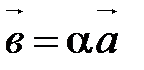 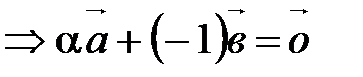. Так как 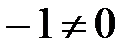, то система векторов  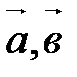линейно зависима. ■

Аналогично, пользуясь теоремой о компланарных векторах, можно доказать свойство

7⁰. Система векторов 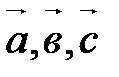 линейно зависима тогда и только тогда, когда эти векторы компланарны.

Базис. Координаты вектора