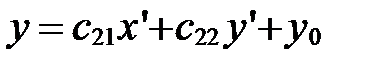Элементы векторной алгебры
Векторы. Линейные операции над векторами
Понятие вектора
Направленным отрезком называется отрезок, у которого указаны начало и конец. Обозначение: 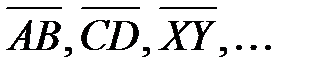
Вектором называется направленный отрезок. Обозначение:  (рис. 1).
(рис. 1).
| А |
| D |
| C |

|
|
|
| Рис. 1 |
Вектор называется нулевым, если его начало и конец совпадают. Обозначение: 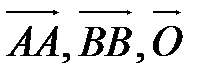 .
.
Векторы  и
и  называются сонаправленными (противоположно направленными), если лучи [ AB ) и [ CD ) сонаправлены (противоположно направлены). Обозначение:
называются сонаправленными (противоположно направленными), если лучи [ AB ) и [ CD ) сонаправлены (противоположно направлены). Обозначение:  (
( 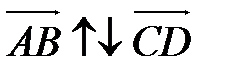 ).
).
На рис. 2  ,
,  .
.
| А |
| В |
| С |
| D |
| K |
| M |
| X |
| Y |
| Рис. 2 |
Векторы 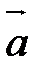 и
и 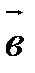 называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Обозначение:
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Обозначение:  ||
|| 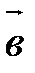 .
.
Нулевой вектор считается коллинеарным любому вектору.
Векторы 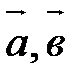 и
и 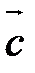 называются компланарными, если существует плоскость, которой они параллельны.
называются компланарными, если существует плоскость, которой они параллельны.
Длиной вектора называется расстояние между его началом и концом. Обозначение длины вектора  :
:  .
.
Длина нулевого вектора равна 0, т.е. 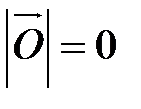 .
.
Вектор называется единичным, если его длина равна единице.
В пространстве существует бесконечное множество единичных векторов.
Два вектора называются равными, если они сонаправлены и длины их равны. Обозначение: 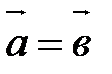 .
.
Два вектора называются противоположными, если они противоположно направлены и длины их равны.
Вектор, противоположный вектору  , обозначается
, обозначается 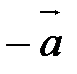 .
.
Откладыванием вектора 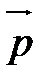 от точки А называется процесс построения такой точки М, что
от точки А называется процесс построения такой точки М, что 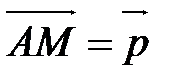 .
.
| В |
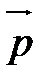 и точка А. Сначала строят луч
и точка А. Сначала строят луч  , исходящий из точки А и сонаправленный с вектором
, исходящий из точки А и сонаправленный с вектором 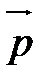 (рис. 3). Затем на луче
(рис. 3). Затем на луче  откладывают с помощью циркуля отрезок АМ, длина которого равна длине вектора
откладывают с помощью циркуля отрезок АМ, длина которого равна длине вектора 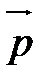 . Вектор
. Вектор  - искомый, т.е.
- искомый, т.е. 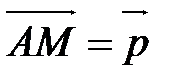 .
.
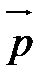
|
| А |
| М |
| Рис. 3 |
§2. Сложение и вычитание векторов
Линейными операциями над векторами называется сложение, вычитание векторов и умножение вектора на число.
Результатом сложения векторов является их сумма. Сумма векторов 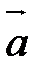 и
и  обозначается
обозначается 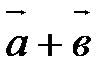 .
.
Существует два правила сложения двух векторов: правило треугольника и правило параллелограмма.
Правило треугольника
Чтобы сложить векторы 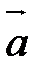 и
и  , надо взять произвольную точку и от нее отложить последовательно сначала вектор
, надо взять произвольную точку и от нее отложить последовательно сначала вектор 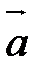 , затем вектор
, затем вектор  . Вектор, начало которого совпадает с началом вектора
. Вектор, начало которого совпадает с началом вектора 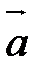 (т.е. первого вектора), а конец – с концом вектора
(т.е. первого вектора), а конец – с концом вектора  (т.е. второго вектора), есть искомая сумма. На рис. 4
(т.е. второго вектора), есть искомая сумма. На рис. 4 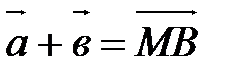 .
.
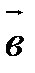
|
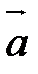
|
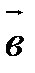
|
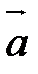
|
| М |
| В |
| Рис. 4 |
По правилу треугольника можно складывать любые векторы.
Коротко правило треугольника можно записать так:
для любых трех точек А,В и С  .
.
Правило параллелограмма
Чтобы сложить векторы 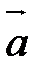 и
и  , надо привести их к общему началу, т.е. взять произвольную точку А, построить такие точки В и С, что
, надо привести их к общему началу, т.е. взять произвольную точку А, построить такие точки В и С, что 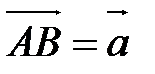 и
и 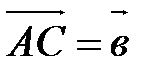 , и достроить полученную фигуру до параллелограмма
, и достроить полученную фигуру до параллелограмма 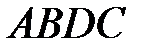 . Вектор
. Вектор  - искомая сумма (рис. 5).
- искомая сумма (рис. 5).

|

|

|

|
| А |
| С |
| В |
| D |
| Рис. 5 |
По правилу параллелограмма можно складывать тольконеколлинеарные векторы.
Свойства сложения векторов:
10. 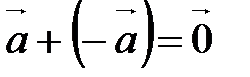
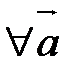 .
.
20. 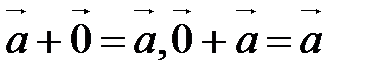
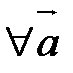 .
.
30. 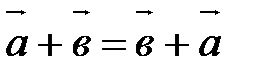
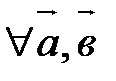 .
.
40. 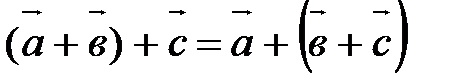
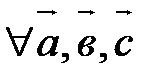 .
.
Суммой трех векторов 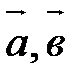 и
и 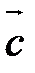 называется вектор
называется вектор 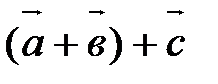 . Учитывая свойство 40, скобки можно опустить и обозначать сумму в виде
. Учитывая свойство 40, скобки можно опустить и обозначать сумму в виде 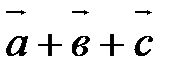 .
.
Суммой n векторов  называется вектор
называется вектор 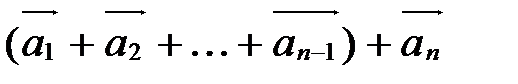 и обозначается так:
и обозначается так: 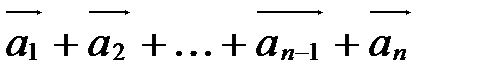 .
.
При построении суммы n векторов пользуются правилом многоугольника.
Правило многоугольника
Чтобы найти сумму n векторов, надо взять произвольную точку и отложить от нее последовательно эти векторы. Вектор, начало которого совпадает с началом первого вектора, а конец – с концом последнего (n-го вектора), есть искомая сумма.
Разностью векторов 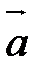 и
и  называется такой вектор
называется такой вектор 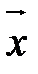 , что
, что  . Разность – это результат вычитания векторов. Разность векторов
. Разность – это результат вычитания векторов. Разность векторов 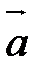 и
и  обозначается так:
обозначается так:  .
.
Умножение вектора на число
Рассмотрим еще одну линейную операцию над векторами – умножение вектора на число. Результатом этой операции является произведение вектора на число.
Произведением вектора 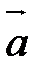 на действительное число a называется вектор
на действительное число a называется вектор  , обозначаемый через
, обозначаемый через  и удовлетворяющий двум условиям:
и удовлетворяющий двум условиям:
1) его длина 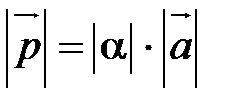 ;
;
2) если a  0, то
0, то 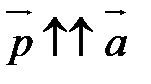 ; если
; если 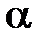 <0, то
<0, то 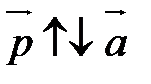 .
.
Алгоритм построения произведения вектора 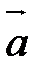 число a таков.
число a таков.
Берем произвольную точку М. Проводим луч 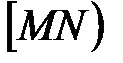 , сонаправленный с вектором
, сонаправленный с вектором 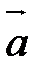 , если a
, если a  0, и противоположно направленный с вектором
0, и противоположно направленный с вектором 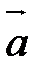 , если
, если 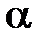 <0. На луче
<0. На луче 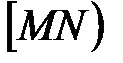 от начала М откладываем отрезок MP, длина которого в
от начала М откладываем отрезок MP, длина которого в 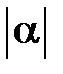 раз больше длины вектора
раз больше длины вектора 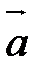 . Вектор
. Вектор 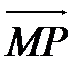 - искомый вектор
- искомый вектор 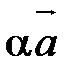 .
.
Продемонстрируем этот алгоритм на конкретном примере. Построим вектор 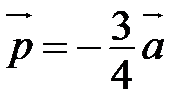 , если
, если 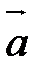 - данный вектор.
- данный вектор.
Возьмем произвольную точку А. Так как 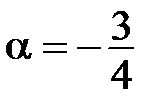 <0, то проводим луч
<0, то проводим луч 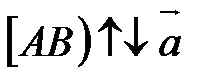 (рис. 7). На луче
(рис. 7). На луче 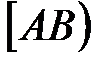 строим такую точку С, что
строим такую точку С, что 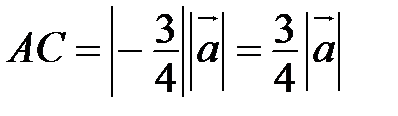 . Тогда
. Тогда 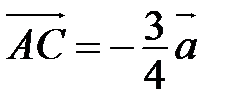 - искомый вектор.
- искомый вектор.
|
| А |
| С |
| В |
| Рис. 7 |
Примеры
1. Система векторов 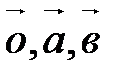 линейно зависима, т.к. если возьмем
линейно зависима, т.к. если возьмем 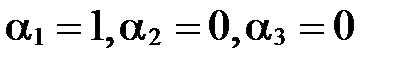 , то получим, что
, то получим, что 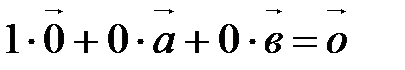 , т.е. существуют такие действительные числа
, т.е. существуют такие действительные числа 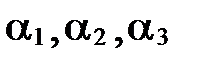 , не все равные 0 одновременно (
, не все равные 0 одновременно ( 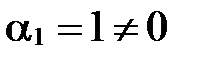 ), что выполняется равенство
), что выполняется равенство 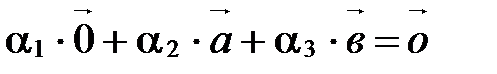 .
.
2. Система двух неколлинеарных векторов 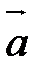 и
и  линейно независима, т.к. сумма двух неколлинеарных векторов
линейно независима, т.к. сумма двух неколлинеарных векторов 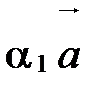 и
и 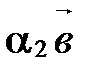 равна нулевому вектору
равна нулевому вектору 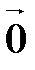 только при
только при  .
.
Базис. Координаты вектора
И их свойства
Множество всех векторов, на котором введена операция сложения векторов, удовлетворяющая свойствам
10. 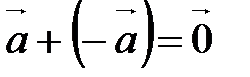 ;
;
20. 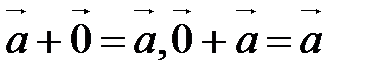 ;
;
30. 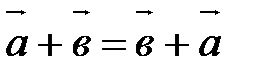 ;
;
40. 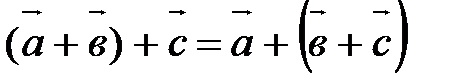 ,
,
и операция умножения вектора на число, удовлетворяющая свойствам
10. 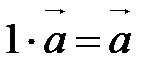 ,
,  ;
;
20. 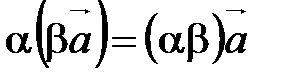 ;
;
30.  ;
;
40. 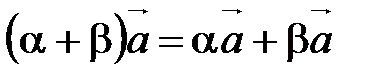 ,
,
называется векторным пространством и обозначается через V.
Базисом векторного пространства называется система векторов, заданных в определенном порядке, которая удовлетворяет условиям:
1) система линейно независима;
2) любой вектор пространства является линейной комбинацией данной системы векторов.
Число векторов базиса называется размерностью векторного пространства.
Выяснить, чему равна размерность векторного пространства V, позволяют следующие две теоремы, которые приведем без доказательства:
Теорема 1. Любая система трех некомпланарных векторов, взятых в определенном порядке, образует базис векторного пространства.
А может ли базис пространства V состоять меньше, чем из трех векторов? Больше, чем из трех векторов? Оказывается, нет, так как справедлива
Теорема 2. Любой базис векторного пространства V состоит из трех векторов.
Эти теоремы можно доказать, пользуясь теоремами о коллинеарных и компланарных векторах и свойствами 20 - 70 линейно зависимой системы векторов.
Из теорем 1 и 2 следует, что размерность векторного пространства V равна 3, поэтому оно называется трехмерным векторным пространством.
Базис, состоящий из векторов 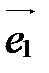 ,
, 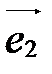 и
и 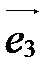 , обозначается так:
, обозначается так:  ,
, 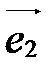 ,
, 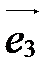 или
или 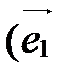 ,
, 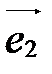 ,
, 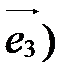 . Векторы
. Векторы 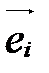 ,
, 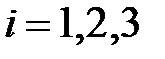 , называются базисными векторами:
, называются базисными векторами:  - первый базисный вектор,
- первый базисный вектор, 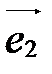 - второй,
- второй, 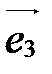 - третий.
- третий.
Пусть 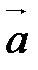 - произвольный вектор пространства V,
- произвольный вектор пространства V, 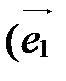 ,
, 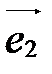 ,
, 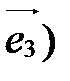 - базис векторного пространства V.
- базис векторного пространства V.
Из теоремы 1 следует, что вектор 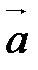 можно разложить по базисным векторам
можно разложить по базисным векторам  ,
, 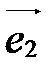 ,
, 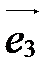 , т.е. существуют такие действительные числа
, т.е. существуют такие действительные числа 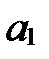 ,
, 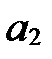 ,
, 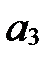 , что
, что
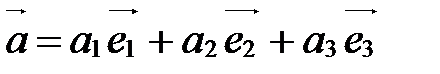 .
.
Коэффициенты 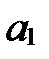 ,
, 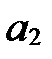 ,
, 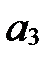 в этом разложении называются координатами вектора
в этом разложении называются координатами вектора 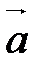 в базисе
в базисе  ,
, 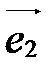 ,
, 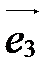 :
: 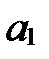 - первая координата,
- первая координата, 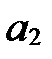 - вторая,
- вторая, 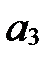 - третья.
- третья.
Обозначают это так: 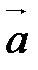 (
( 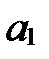 ;
; 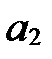 ;
; 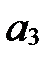 )
)  ,
, 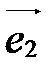 ,
, 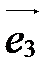 .
.
Когда ясно, о каком базисе идет речь, пишут так: 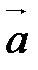 (
( 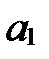 ;
; 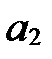 ;
; 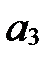 ).
).
Свойства координат векторов
10. Нулевой вектор в любом базисе имеет нулевые координаты: 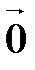 (0;0;0).
(0;0;0).
□ Разложим  по векторам базиса
по векторам базиса  ,
, 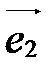 ,
, 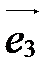 :
:
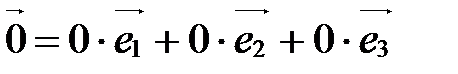 .
.
Следовательно, 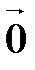 (0;0;0)
(0;0;0)  ,
, 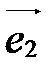 ,
, 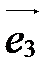 . ■
. ■
20. Если  ,
, 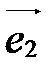 ,
, 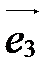 - базис пространства V, то
- базис пространства V, то 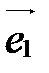 (1;0;0),
(1;0;0), 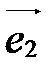 (0;1;0),
(0;1;0), 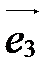 (0;0;1).
(0;0;1).
□ 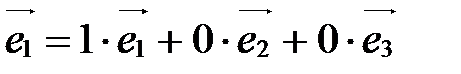
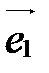 (1;0;0);
(1;0;0);
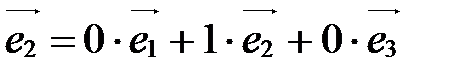
 (0;1;0);
(0;1;0);
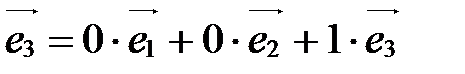
 (0;0;1). ■
(0;0;1). ■
30. Если 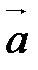 (
( 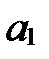 ;
; 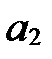 ;
; 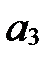 ),
),  в базисе
в базисе  ,
, 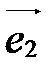 ,
, 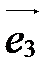 , а
, а 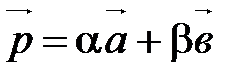 , то
, то
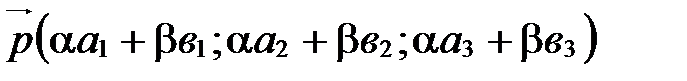
в базисе  ,
,  ,
,  (координаты линейной комбинации векторов равны линейным комбинациям их соответствующих координат).
(координаты линейной комбинации векторов равны линейным комбинациям их соответствующих координат).
□ По определению координат вектора
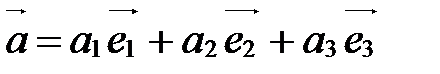 ,
, 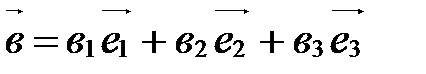 .
.
Тогда  ,
, 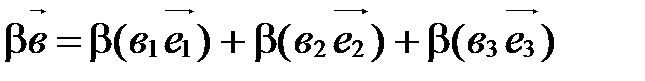 .
.
Сложим почленно эти равенства и воспользуемся свойствами сложения векторов и умножения вектора на число:
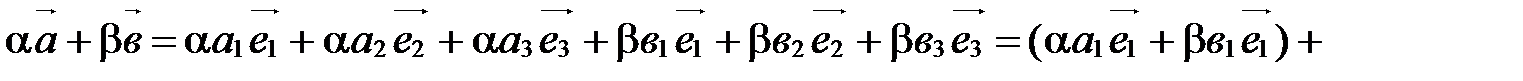
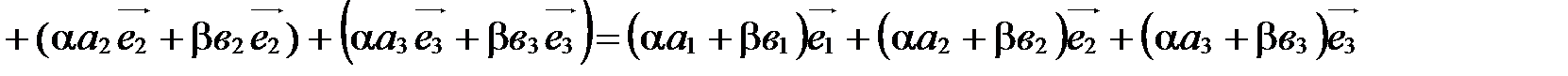 .
.
По определению координат вектора
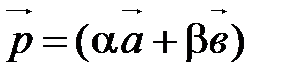
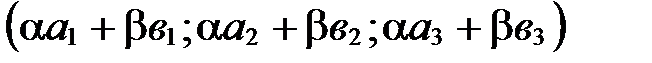 . ■
. ■
Из свойства 30 получаем следствия:
Следствие 1. Каждая координата суммы (разности) двух векторов равна сумме (разности) соответствующих координат этих векторов.
Следствие 2. При умножении вектора на число каждая его координата умножается на это число.
□ Чтобы доказать справедливость следствия 1, надо в свойстве 30 взять сначала a=b=1, а затем a=1, b=-1. Для доказательства следствия 2 полагаем b=0. ■
40. Векторы равны тогда и только тогда, когда равны их соответствующие координаты: 

 ,
, 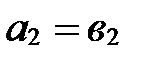 ,
, 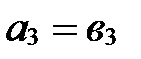 .
.
50. Пусть 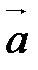 (
( 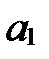 ;
; 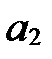 ;
; 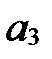 ),
), 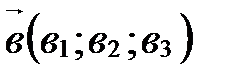 ,
, 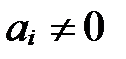 и
и 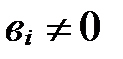 , i =1, 2, 3. Векторы
, i =1, 2, 3. Векторы 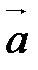 и
и 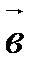 коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны:
коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны:
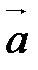 ||
|| 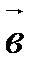

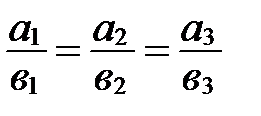 .
.
Пусть 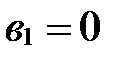 . Тогда
. Тогда
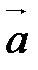 ||
|| 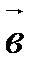

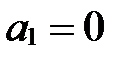 и
и 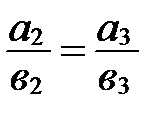 .
.
Если же  , то
, то
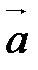 ||
|| 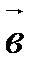

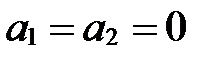 , а
, а 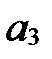 и
и 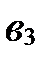 - любые.
- любые.
Частным случаем произвольного базиса является ортонормированный базис. Его удобно использовать при решении метрических задач (т.е. задач, связанных с вычислением длин отрезков (векторов) и величин углов).
| Е1 |
| Е3 |
| О |
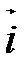
|
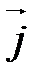
|

|
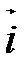 ,
, 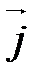 ,
, 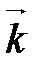 называется ортонормированным, если его векторы удовлетворяют двум условиям:
называется ортонормированным, если его векторы удовлетворяют двум условиям:
1) 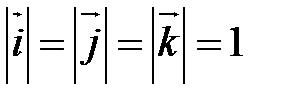 ;
;
| Рис. 8 |
| Е2 |
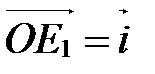 ,
, 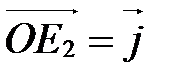 ,
, 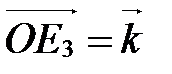 (рис. 8), то углы
(рис. 8), то углы  ,
,  и
и 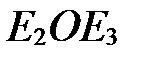 - прямые.
- прямые.
|
|
| Рис. 9 |
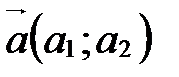 . Ортонормированный базис выглядит так:
. Ортонормированный базис выглядит так: 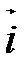 ,
, 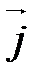 (рис. 9).
(рис. 9).
Нелинейные операции над векторами
Геометрические свойства
Алгебраические свойства
Приложение скалярного произведения
Геометрические свойства
Алгебраические свойства
Геометрические свойства
Алгебраические свойства
Трех векторов
Смешанное произведение векторов применяется:
1. Для выяснения компланарности трех векторов:
векторы  ,
, 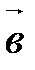 ,
, 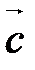 компланарны тогда и только тогда, когда
компланарны тогда и только тогда, когда  .
.
2. Для вычисления объема параллелепипеда:  (рис. 28).
(рис. 28).
| Рис. 28 |
| Рис. 29 |
| А1 |
| D1 |
| С1 |
| В1 |
| D |
| С |
| В |
| А |
| А1 |
| В1 |
| С1 |
| А |
| В |
| С |
| Рис. 30 |
| D |
| А |
| В |
| С |
3. Для вычисления объема треугольной призмы:
 (рис. 29).
(рис. 29).
4. Для вычисления объема тетраэдра (треугольной пирамиды):
 (рис. 30).
(рис. 30).
Задания для самостоятельной работы
1. Вычислите 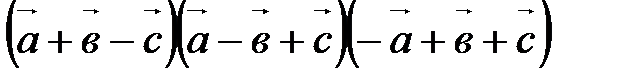 , если
, если 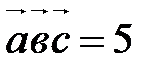 .
.
2. Докажите, что если  ||
||  , то
, то  .
.
3. Выясните, какой является тройка векторов  ,
,  ,
, 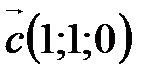 (левой или правой).
(левой или правой).
4. Докажите, что векторы  ,
, 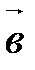 ,
, 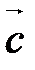 , удовлетворяющие условию
, удовлетворяющие условию 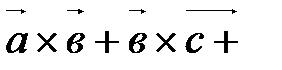
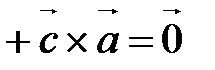 ,компланарны.
,компланарны.
5. Найдите объем треугольной призмы АВСА1В1С1, если  ,
, 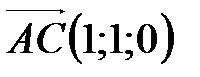 ,
, 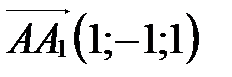 .
.
6. Найдите объем тетраэдра ABCD, если 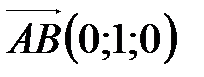 ,
, 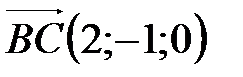 ,
, 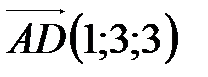 .
.
Метод координат
Системы координат
Систем координат
| О |
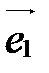
|
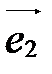
|

|
| Рис. 31 |
| О |
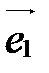
|
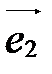
|

|
| х |
| у |
| z |
| Рис. 32 |
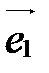 ,
,  ,
, 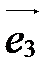 в пространстве, называется аффинной системой координат в пространстве и обозначается
в пространстве, называется аффинной системой координат в пространстве и обозначается  или
или 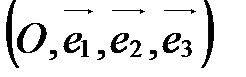 (рис. 31).
(рис. 31).
Точка О называется началом координат, векторы 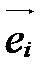 ,
, 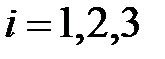 , - координатными векторами:
, - координатными векторами: 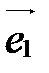 - первый координатный вектор,
- первый координатный вектор,  - второй,
- второй, 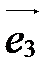 - третий.
- третий.
Направленные прямые, на которых положительное направление определяется базисными векторами и которые проходят через точку О, называются координатными осями:
 - ось абсцисс;
- ось абсцисс;
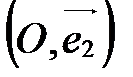 - ось ординат;
- ось ординат;
 - ось аппликат (рис. 32).
- ось аппликат (рис. 32).
Оси абсцисс, ординат и аппликат обозначаются и так: Ох, Оу, О z.
Плоскости, определяемые осями Ох и Оу, Оу и О z, Ох и О z, называются координатными плоскостями и обозначаются Оху, Оу z, Oxz, а систему координат  иногда обозначают Oxyz.
иногда обозначают Oxyz.
| Рис. 33 |
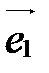
|
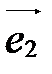
|

|
| О |
| М |
 - аффинная система координат, М – произвольная точка пространства. Вектор
- аффинная система координат, М – произвольная точка пространства. Вектор  называется радиус-вектором точки М относительно точки О (рис. 33).
называется радиус-вектором точки М относительно точки О (рис. 33).
Понятие координат точки вводится на основе понятия координат вектора.
Координатами точки М в системе координат  называются координаты ее радиус-вектора
называются координаты ее радиус-вектора  в базисе
в базисе 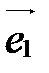 ,
,  ,
, 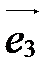 .
.
Обозначение  или просто М(х;у; z ): х – абсцисса точки М, у – ордината, z – аппликата.
или просто М(х;у; z ): х – абсцисса точки М, у – ордината, z – аппликата.
Если в пространстве задана аффинная система координат, то устанавливается взаимно однозначное соответствие между точками пространства и упорядоченными тройками (х;у; z ) действительных чисел.
Рассмотрим особенности расположения точки относительно аффинной системы координат, если некоторые ее координаты являются нулевыми. Пусть М(х;у; z ).
1) Если z=0, то М(х;у;0) Þ  Þ
Þ 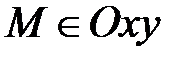 . Верно и обратное:
. Верно и обратное: 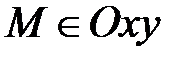 Þ z=0.
Þ z=0.
2) Докажите самостоятельно, что если у=0, то  , и наоборот, если
, и наоборот, если  , то у=0.
, то у=0.
3) Докажите самостоятельно, что если х=0, то 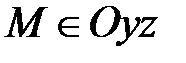 , и наоборот, если
, и наоборот, если 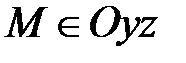 , то х=0.
, то х=0.
4) Если z=0 и у=0, то 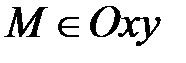 и
и  Þ
Þ  Þ
Þ 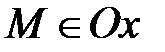 . Верно и обратное:
. Верно и обратное: 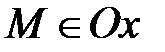 Þ z=0 и у=0.
Þ z=0 и у=0.
Докажите самостоятельно, что:
5) Если х=0 и у=0, то 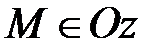 и наоборот, если
и наоборот, если 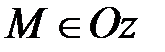 , то х=0 и у=0.
, то х=0 и у=0.
6) Если х=0 и z=0, то 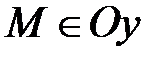 и наоборот, если
и наоборот, если 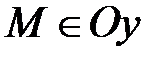 , то х=0 и z=0.
, то х=0 и z=0.
7) Так как 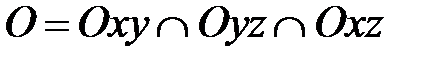 , то из пунктов 1) – 3) следует, что О(0;0;0) в системе координат
, то из пунктов 1) – 3) следует, что О(0;0;0) в системе координат 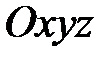 .
.
Чтобы построить точку М(х;у; z ) по ее координатам в системе координат  , надо сначала построить точку М1(х;0;0), затем точку М2(х;у;0), а затем точку М(х;у;z). Процесс построения этих точек показан на рис. 34. Ломаная ОМ1М2М называется координатной ломаной точки М.
, надо сначала построить точку М1(х;0;0), затем точку М2(х;у;0), а затем точку М(х;у;z). Процесс построения этих точек показан на рис. 34. Ломаная ОМ1М2М называется координатной ломаной точки М.
| М1 |
| М |
| М2 |
| О |
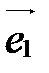
|
|

|
| Рис. 34 |
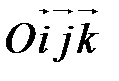 или
или  , где
, где 
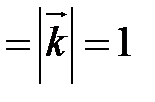 ,
,  ,
, 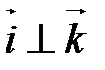 и
и  .
.
Прямоугольная декартова система координат является частным случаем аффинной.
Замечание. На плоскости аффинная система координат состоит из точки О (начала координат) и двух базисных векторов 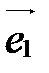 и
и  (координатных векторов) (рис. 35). Поэтому в системе координат на плоскости любая точка имеет две координаты
(координатных векторов) (рис. 35). Поэтому в системе координат на плоскости любая точка имеет две координаты 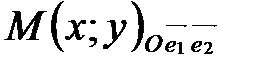 . Прямоугольная декартова система координат на плоскости изображена на рис. 36.
. Прямоугольная декартова система координат на плоскости изображена на рис. 36.
| О |
| О |
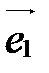
|
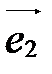
|

|
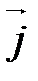
|
| Рис. 35 |
| Рис. 36 |
Основные аффинные задачи
1. Координаты вектора, заданного двумя точками.
Теорема 1. Если в аффинной системе координат 
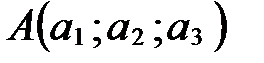 и
и 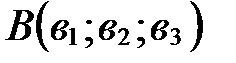 , то
, то  .
.
Представим вектор  в виде разности векторов
в виде разности векторов 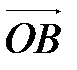 и
и 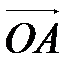 :
:
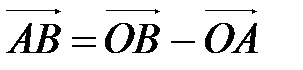 .
.
Так как 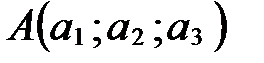 , то по определению координат точки
, то по определению координат точки 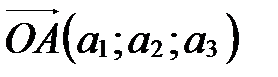 . Аналогично
. Аналогично 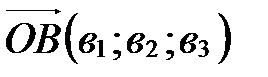 . Применяя свойство координат векторов (координаты разности двух векторов равны разности их соответствующих координат), получаем, что вектор
. Применяя свойство координат векторов (координаты разности двух векторов равны разности их соответствующих координат), получаем, что вектор 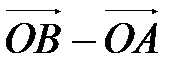 имеет координаты
имеет координаты 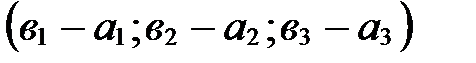 Þ
Þ  .
.
2. Деление отрезка в данном отношении.
Говорят, что точка М делит направленный отрезок 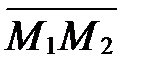 в отношении
в отношении  , если выполняется векторное равенство:
, если выполняется векторное равенство:
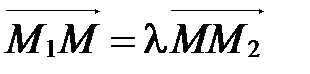 . (1)
. (1)
Число  при этом называется простым отношением трех точек М1, М2 и М. Простое отношение трех точек М1, М2 и М обозначается так:
при этом называется простым отношением трех точек М1, М2 и М. Простое отношение трех точек М1, М2 и М обозначается так:  .
.
Почему в определении деления отрезка в данном отношении  ?
?
Пусть М1 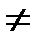 М2 и точка М делит направленный отрезок
М2 и точка М делит направленный отрезок 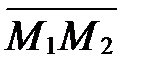 в отношении l=-1. Тогда по определению деления отрезка в данном отношении
в отношении l=-1. Тогда по определению деления отрезка в данном отношении
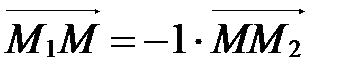 ,
,
т.е.  Þ
Þ 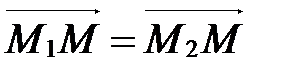 Þ
Þ 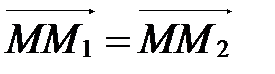 . А так как начало у векторов
. А так как начало у векторов 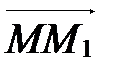 и
и 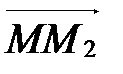 общее и они равны, то М1=М2. Получили противоречие с условием, следовательно,
общее и они равны, то М1=М2. Получили противоречие с условием, следовательно,  .
.
Из векторного равенства (1) следует, что если  , то
, то 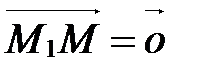 , т.е. точка М совпадает с точкой М1; если l>0, то точка М лежит внутри отрезка
, т.е. точка М совпадает с точкой М1; если l>0, то точка М лежит внутри отрезка 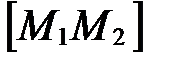 (рис. 37), т.е.
(рис. 37), т.е. 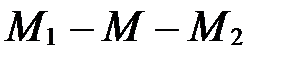 ; если l<0, то точка М лежит на прямой
; если l<0, то точка М лежит на прямой 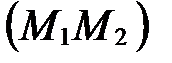 вне отрезка
вне отрезка 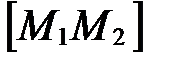 (рис. 38), т.е.
(рис. 38), т.е.  или
или 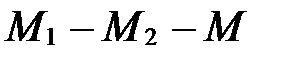 .
.
| М1 |
| М |
| М2 |
| Рис. 37 |
| М |
| М1 |
| М2 |
| М2 |
| М1 |
| М |
| Рис. 38 |
Теорема 2. Пусть в аффинной системе координат 
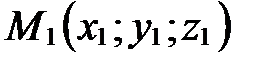 ,
, 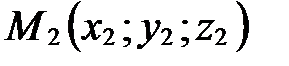 . Тогда координаты точки
. Тогда координаты точки 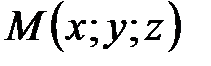 , делящей направленный отрезок
, делящей направленный отрезок 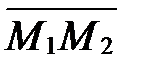 в отношении
в отношении 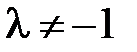 , находятся по формулам:
, находятся по формулам:
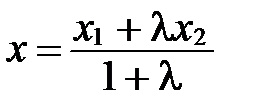 ;
; 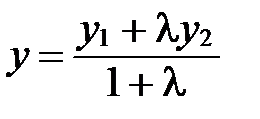 ;
;  . (2)
. (2)
По определению деления отрезка в данном отношении 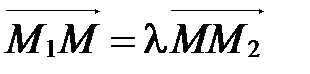 .
.
| О |
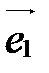
|
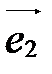
|
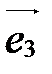
|
| М1 |
| М |
| М2 |
| Рис. 39 |
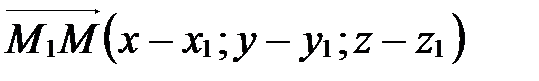 ,
, 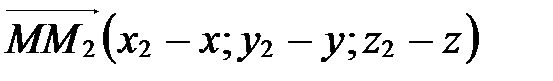 . Тогда
. Тогда 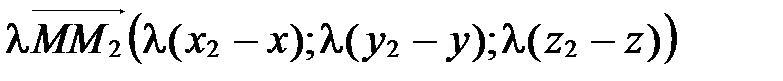 . Так как два вектора равны тогда и только тогда, когда равны их соответствующие координаты, то
. Так как два вектора равны тогда и только тогда, когда равны их соответствующие координаты, то 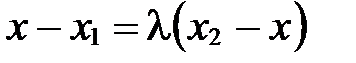 ;
; 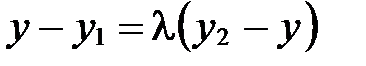 ;
; 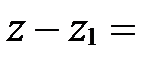
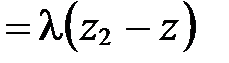 , откуда получаем:
, откуда получаем: 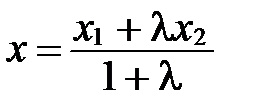 ;
; 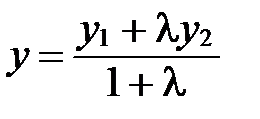 ;
;  .
.
Формулы (2) называются формулами деления отрезка в данном отношении в координатах.
Из теоремы 2 получаем
Следствие. Если М(х;у; z ) – середина отрезка М1М2 с концами 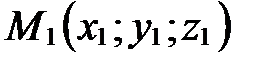 и
и 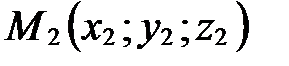 , то
, то  ,
, 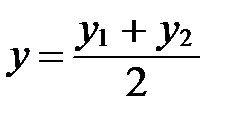 ,
,  .
.
Так как М – середина М1М2, то  Þ l=1. Применяя формулы деления отрезка в данном отношении в координатах, получаем:
Þ l=1. Применяя формулы деления отрезка в данном отношении в координатах, получаем:
 ,
, 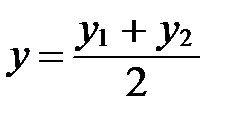 ,
,  .
.
Основная метрическая задача
Теорема 3(расстояние между двумя точками в координатах). Если в прямоугольной декартовой системе координат 
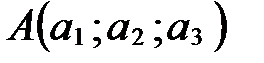 ,
, 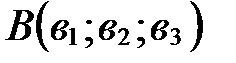 , то расстояние АВ между точками А и В находится по формуле:
, то расстояние АВ между точками А и В находится по формуле:
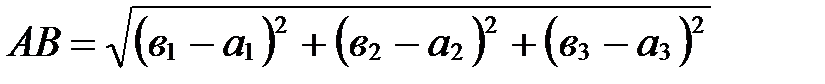 .
.
Учитывая, что  ,
,  и используя формулы для нахождения длины вектора в координатах, получаем:
и используя формулы для нахождения длины вектора в координатах, получаем:
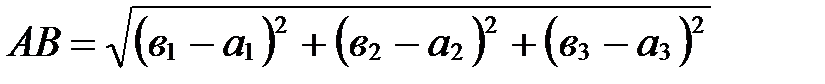 .
.
Формулы, доказанные в теоремах 1 и 2, можно использовать и в аффинной, и в прямоугольной декартовой системе координат, а формулу из теоремы 3 – только в прямоугольной декартовой системе координат.
Формулы преобразования координат
§12. Преобразование аффинной системы координат
| О |
| О' |
| М |

|
|
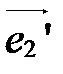
|

|
| Рис. 40 |
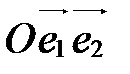 и
и  . Первую назовем старой, вторую - новой. Пусть М – произвольная точка плоскости, которая в старой системе
. Первую назовем старой, вторую - новой. Пусть М – произвольная точка плоскости, которая в старой системе 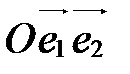 имеет координаты х,у, а в новой системе
имеет координаты х,у, а в новой системе  - координаты
- координаты  (рис. 40).
(рис. 40).
Задача преобразования координат состоит в следующем: зная координаты нового начала и новых координатных векторов в старой системе:
 ,
, 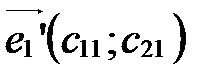 ,
,  , (3)
, (3)
выразить координаты х,у точки М в старой системе координат, через координаты  этой точки в новой системе.
этой точки в новой системе.
Из формул (3) следует, что
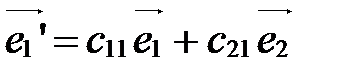 ;
; 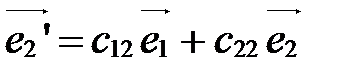 ;
; 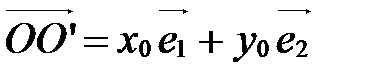 . (4)
. (4)
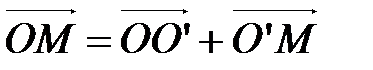 (по правилу треугольника).
(по правилу треугольника).
Так как 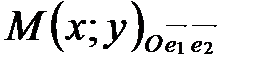 ,
,  , то по определению координат точки
, то по определению координат точки  ,
, 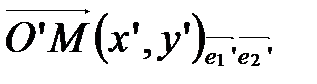 , т.е.
, т.е. 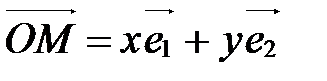 ;
; 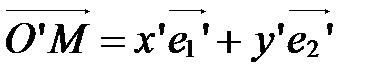 .
.
Тогда, используя формулы (4), получим:
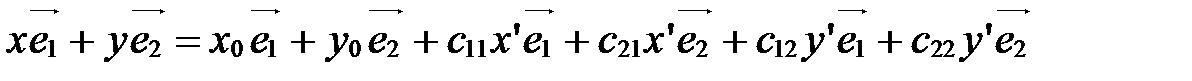 ,
,
т.е. 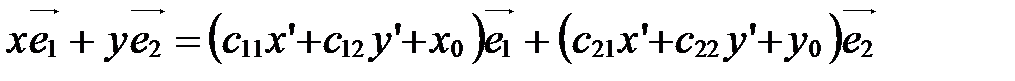 ,
,
откуда находим:
 ; ;
|
. Так выражаются координаты х,у произвольной точки М в старой системе  через ее координаты
через ее координаты  в новой системе
в новой системе  .
.
Формулы (5) называются формулами преобразования аффинной системы координат.
Коэффициенты 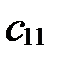 ,
,  при
при 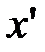 - координаты нового вектора
- координаты нового вектора  в старой системе
в старой системе  ; коэффициенты
; коэффициенты  ,
, 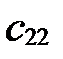 при
при  - координаты нового вектора
- координаты нового вектора 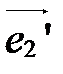 в старой системе, свободные члены
в старой системе, свободные члены 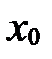 ,
, 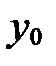 - координаты нового начала
- координаты нового начала 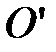 в старой системе:
в старой системе:
Координаты точки М
в новой системе 
| х |
| у |
| = |
| = |
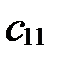
|

|
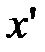
|
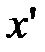
|
| + |
| + |

|
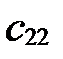
|

|

|
| + |
| + |
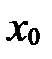
|
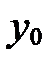
|
Координаты точки М в старой системе 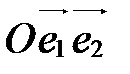
|
Координаты нового вектора  в старой системе в старой системе 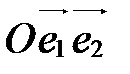
|
Координаты нового вектора 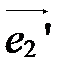 в старой системе в старой системе 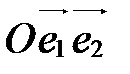
|
Координаты нового начала 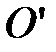 в старой системе в старой системе 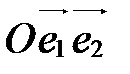
|
Таблица 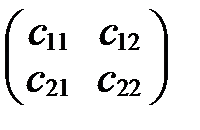 называется матрицей перехода от базиса
называется матрицей перехода от базиса  ,
,  к базису
к базису  ,
,  .
.
Частные случаи преобразования аффинной
Системы координат
1. Перенос начала.
При этом преобразовании 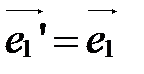 ,
,  , а
, а  (рис. 41).
(рис. 41).
Найдем координаты векторов  и
и  в старой системе, т.е.
в старой системе, т.е. 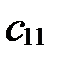 ,
,  ,
, 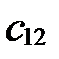 и
и 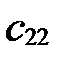 :
:
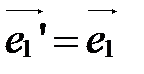 Þ
Þ  Þ
Þ 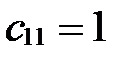 ,
, 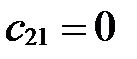 ;
;
 Þ
Þ 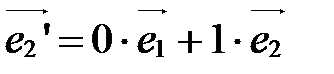 Þ
Þ 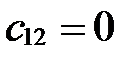 ,
, 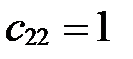 .
.
Тогда формулы (5) примут вид:
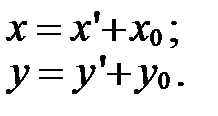
|
| (6) |
Формулы (6) называются формулами переноса начала.
| О |
| О' |

|
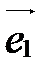
|
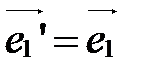
|
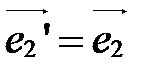
|
| Рис. 41 |
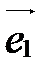
|

|
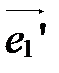
|
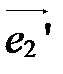
|
| О'=О |
| Рис. 42 |
2. Замена координатных векторов.
При этом преобразовании системы координат имеют общее начало и отличаются координатными векторами (рис. 42).
Так как  , то
, то 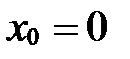 ,
, 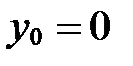 . Тогда формулы (5) примут вид:
. Тогда формулы (5) примут вид:
 ; ;
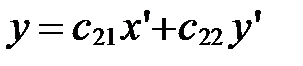 . .
|
| (7) |
Формулы (7) называются формулами замены координатных векторов.
Полярные координаты
Если указано правило, по которому положение точек плоскости можно определить с помощью упорядоченных пар действительных чисел, то говорят, что на плоскости задана система координат. Кроме аффинной системы координат, которая была рассмотрена в §10, в математике часто применяют полярную систему координат на плоскости.
Система полярных координат вводится на ориентированной плоскости.
Пара, состоящая из точки О и единичного вектора 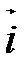 , называется полярной системой координат и обозначается
, называется полярной системой координат и обозначается  или
или 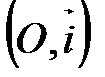 . Направленная прямая
. Направленная прямая  называется полярной осью, точка О - полюсом (рис. 49).
называется полярной осью, точка О - полюсом (рис. 49).
| Р |
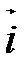
|
| Рис. 49 |
| О |
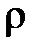 от точки О до точки М называется полярным радиусом точки М.
от точки О до точки М называется полярным радиусом точки М.
 . .
|
Таким образом, 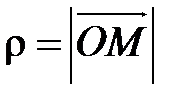 . Если М совпадает с О, то
. Если М совпадает с О, то 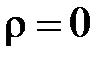 . Для любой точки М ее полярный радиус
. Для любой точки М ее полярный радиус
| О |
| Р |
|
| Рис. 50 |
| М |
| j |
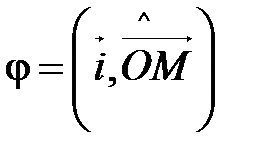 называется полярным углом точки М (рис. 50).
называется полярным углом точки М (рис. 50).
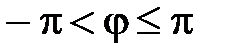 . .
|
Если М совпадает с полюсом О, то j - неопределенный. Из определения направленного угла между векторами (см. §13) следует, что полярный угол
| Рис. 51 |
| О |
| Р |
|
| С |
| А |
| В |
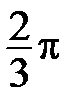
|
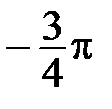
|
На рис. 51 построены точки 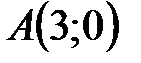 ,
, 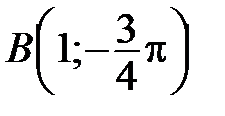 ,
, 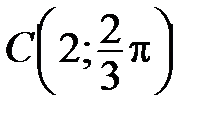 по их полярным координатам.
по их полярным координатам.
| О |
| Р |
|
| Рис. 52 |
| М |
| j |
|
| М1 |
Выведем формулы перехода от полярных координат к прямоугольным декартовым и обратно.
Пусть 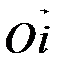 - полярная система координат на ориентированной плоскости,
- полярная система координат на ориентированной плоскости, 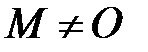 ,
, 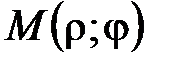 в
в 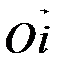 . Присоединим к полярной системе
. Присоединим к полярной системе 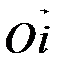 единичный вектор
единичный вектор  , ортогональный вектору
, ортогональный вектору 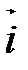 так, чтобы базис
так, чтобы базис 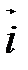 ,
, 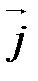 был правым (рис. 52).
был правым (рис. 52).
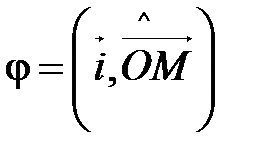 ,
, 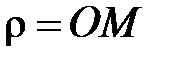 .
.
Пусть М(х;у) в  . Тогда
. Тогда  ;
; 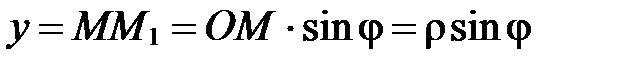 (рис. 52).
(рис. 52).
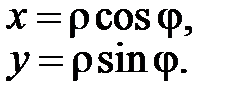
|
Получили формулы перехода от полярных координат к прямоугольным:
Возведем обе части этих равенств в квадрат и сложим:
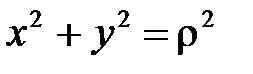 , откуда
, откуда 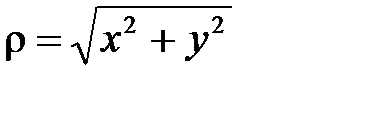 (корень берется со знаком «+», т.к.
(корень берется со знаком «+», т.к. 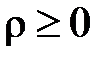 ).
).  Þ
Þ 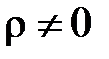 Þ
Þ 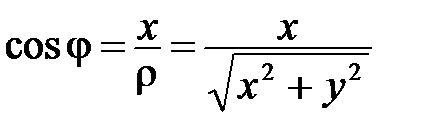 ;
; 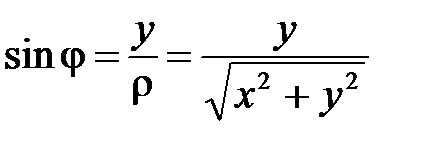 .
.
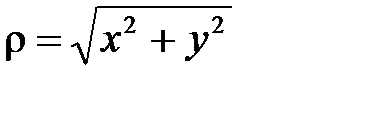 , ,
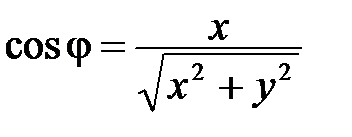 , ,
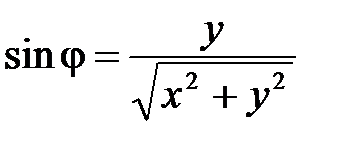 . .
|
Получили формулы перехода от прямоугольных декартовых координат к полярным:
| О |
| a |
| О |
| в |
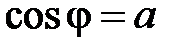
|
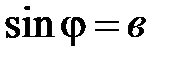
|
| Рис. 53 |
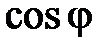 или только
или только 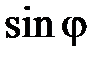 , т.к. по одной тригонометрической функции определить полярный угол однозначно невозможно: в промежутке
, т.к. по одной тригонометрической функции определить полярный угол однозначно невозможно: в промежутке 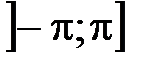 существуют два угла с одинаковыми косинусами (два угла с одинаковыми синусами) (рис. 53). Поэтому правильно найти полярный угол j вы сможете, только если одновременно вычислите
существуют два угла с одинаковыми косинусами (два угла с одинаковыми синусами) (рис. 53). Поэтому правильно найти полярный угол j вы сможете, только если одновременно вычислите 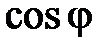 и
и 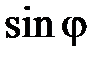 .
.
Прямая линия на плоскости
Различные уравнения прямой
Говорят, что уравнение 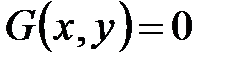 есть уравнение линии
есть уравнение линии 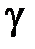 , если выполняются два условия:
, если выполняются два условия:
1) если точка 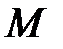 принадлежит линии
принадлежит линии 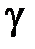 , то ее координаты удовлетворяют уравнению
, то ее координаты удовлетворяют уравнению 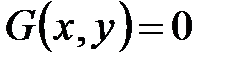 ;
;
2) если координаты точки 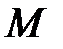 удовлетворяют уравнению
удовлетворяют уравнению 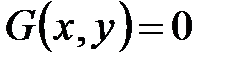 , то
, то  .
.
Заметим, что условие 2) можно заменить на эквивалентное ему условие 2*):
2*) если  , то ее координаты не удовлетворяют уравнению
, то ее координаты не удовлетворяют уравнению 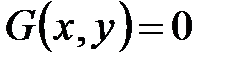 .
.
Линия на плоскости называется алгебраической, если в какой-либо аффинной системе координат уравнение этой линии можно представить в 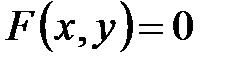 , где
, где 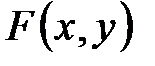 - многочлен от переменных
- многочлен от переменных 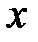 и
и 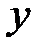 , т.е. сумма членов вида
, т.е. сумма членов вида 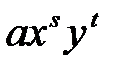 ,
, 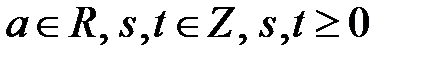 .
.
Число 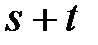 называется степенью члена
называется степенью члена 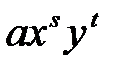 , где
, где 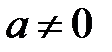 .
.
Наивысшая степень членов многочлена 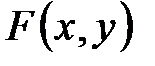 называется степенью этого многочлена. Например, степень многочлена
называется степенью этого многочлена. Например, степень многочлена 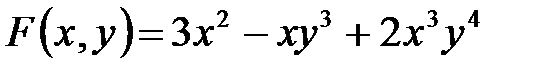 равна 7.
равна 7.
Порядком алгебраической линии, заданной уравнением 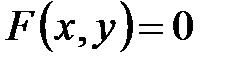 , называется степень многочлена
, называется степень многочлена 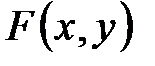 .
.
Из школьного курса известно, что прямая линия является линией первого порядка, а окружность, гипербола и парабола – линиями второго порядка.
Рассмотрим на плоскости прямую линию. Любой ненулевой вектор, параллельный данной прямой, называется ее направляющим вектором. Направляющий вектор прямой  будем обозначать через
будем обозначать через 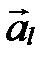 . Прямая имеет бесконечное множество направляющих векторов. Любые два из них коллинеарны (рис. 54).
. Прямая имеет бесконечное множество направляющих векторов. Любые два из них коллинеарны (рис. 54).
Прямая на плоскости однозначно задается точкой и направляющим вектором или двумя точками.
Выведем несколько уравнений прямой на плоскости в аффинной системе координат  .
.
| l |
| Рис. 54 |
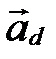
|
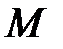
|
| Рис. 55 |

|
| d |
1. Каноническое уравнение прямой.
Пусть прямая  задана точкой
задана точкой 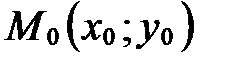 и направляющим вектором
и направляющим вектором  (рис. 55). Этот факт будем обозначать так:
(рис. 55). Этот факт будем обозначать так: 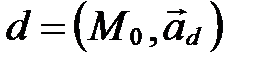 .
.
Если точка 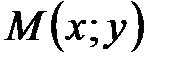 принадлежит прямой
принадлежит прямой  , то
, то 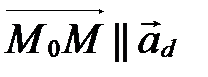 . Находим координаты вектора
. Находим координаты вектора 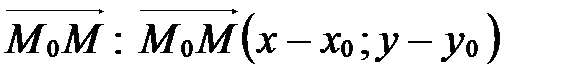 . Далее применяем условие коллинеарности двух векторов в координатах (см. § 5, свойство координат векторов 50):
. Далее применяем условие коллинеарности двух векторов в координатах (см. § 5, свойство координат векторов 50):
 , если
, если 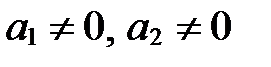 ;
;
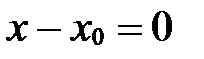 , если
, если  ;
;
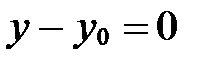 , если
, если 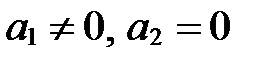 .
.
Если  , то
, то 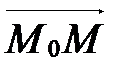 ||
|| 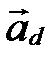 . Следовательно,
. Следовательно,
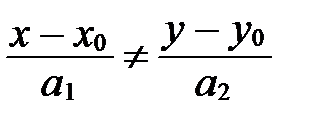 , если
, если 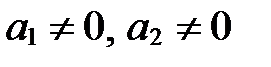 ;
;
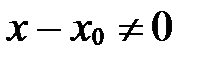 , если
, если  ;
;
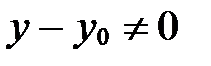 , если
, если 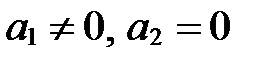 .
.
 принадлежит прямой
принадлежит прямой  тогда и только тогда, когда ее координаты удовлетворяют уравнению
тогда и только тогда, когда ее координаты удовлетворяют уравнению
 (если
(если 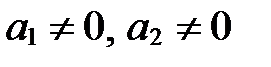 ); (10)
); (10)
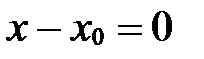 (если
(если  ); (11)
); (11)
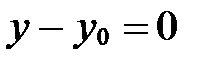 (если
(если 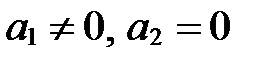 ). (12)
). (12)
Каждое из уравнений (10), (11) и (12) называется каноническим уравнением прямой на плоскости.
В уравнениях (10)-(12) 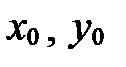 - координаты фиксированной точки
- координаты фиксированной точки 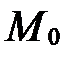 прямой
прямой  ;
; 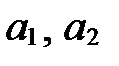 - координаты направляющего вектора прямой
- координаты направляющего вектора прямой  ;
;  - текущие координаты произвольной точки прямой
- текущие координаты произвольной точки прямой  .
.
2. Параметрическое уравнение прямой.
Пусть прямая  задана точкой
задана точкой 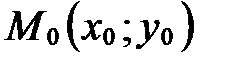 и направляющим вектором
и направляющим вектором  .
.
 (рис. 54)
(рис. 54) 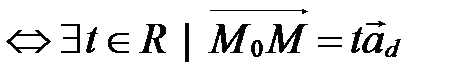 (по теореме о коллинеарных векторах).
(по теореме о коллинеарных векторах).
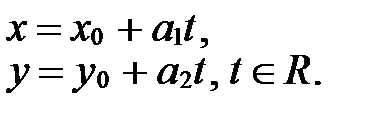
|
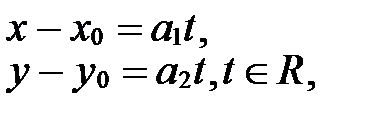 или (13)
или (13)
Система уравнений (13) называется параметрическим уравнением прямой на плоскости. Действительное число 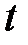 называется параметром. Геометрический смысл параметра
называется параметром. Геометрический смысл параметра 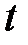 состоит в следующем: для любой точки
состоит в следующем: для любой точки 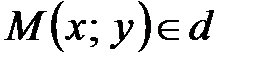 существует единственный параметр
существует единственный параметр 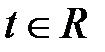 , удовлетворяющий уравнениям (13), и обратно,
, удовлетворяющий уравнениям (13), и обратно, 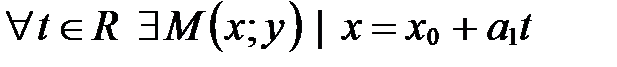 и
и  .
.
3. Уравнение прямой, заданной двумя точками.
Пусть 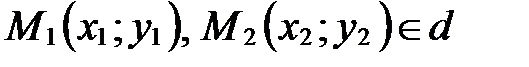 (рис. 56). Тогда в качестве направляющего вектора прямой
(рис. 56). Тогда в качестве направляющего вектора прямой  можно взять вектор
можно взять вектор 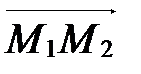 , т.е.
, т.е.
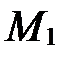
|
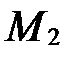
|
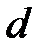
|
| Рис. 56 |
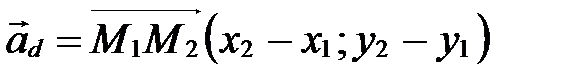 .
.
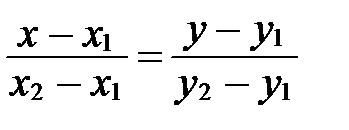
|
 задана точкой
задана точкой 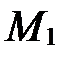 и направляющим вектором
и направляющим вектором  . Применяем каноническое уравнение прямой (10) (см. пункт 1):
. Применяем каноническое уравнение прямой (10) (см. пункт 1):
(14)
Уравнение (14) называется уравнением прямой, заданной на плоскости двумя точками 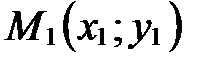 и
и 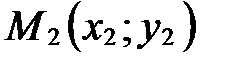 .
.
Заметим, что если  или
или 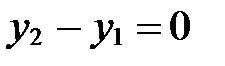 , то применяем частные случаи (11) или (12) канонического уравнения прямой.
, то применяем частные случаи (11) или (12) канонического уравнения прямой.
4. Уравнение прямой в «отрезках».
| О |
| y |
| d |
| x |
|
|
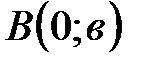
|
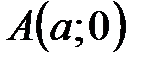
|
| Рис. 57 |
 пересекает ось
пересекает ось  аффинной системы координат
аффинной системы координат 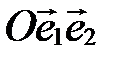 в точке
в точке 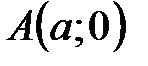 , ось
, ось 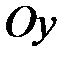 - в точке
- в точке 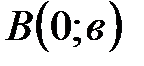 , где
, где  (рис. 57).
(рис. 57).
Применяя уравнение прямой, заданной двумя точками А и В, получим:
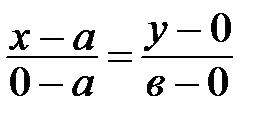 ;
;
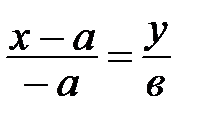 ;
;  ,
,
откуда получаем уравнение:
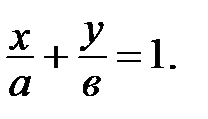 (15)
(15)
Уравнение (15) называется уравнением прямой «в отрезках».
Геометрический смысл а и в в уравнении прямой «в отрезках»: а – это абсцисса точки пересечения прямой  с осью
с осью  , в – ордината точки пересечения прямой
, в – ордината точки пересечения прямой  с осью
с осью 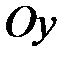 аффинной системы координат.
аффинной системы координат.
5. Уравнение прямой, заданной точкой и угловым коэффициентом.
| О |
| y |
| d |
| x |
|
|
| Рис. 58 |
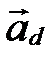
|
| М0 |
 - прямая, не параллельная оси
- прямая, не параллельная оси 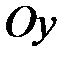 (рис. 58),
(рис. 58), 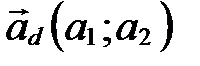 - направляющий вектор прямой
- направляющий вектор прямой  . Так как
. Так как  ||
|| 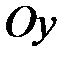 , а
, а 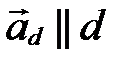 , то
, то 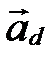 ||
|| 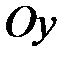 . Следовательно,
. Следовательно, 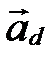 ||
|| 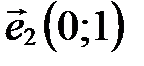 . Поэтому
. Поэтому 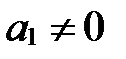 (см. условие коллинеарности векторов в координатах).
(см. условие коллинеарности векторов в координатах).
Число 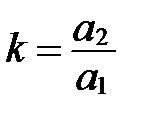 называется угловым коэффициентом прямой
называется угловым коэффициентом прямой  .
.
Угловой коэффициент прямой не зависит от выбора направляющего вектора этой прямой (попробуйте доказать это самостоятельно).
| О |
| y |
| d |
| x |
|

|
| Рис. 59 |
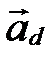
|
| j |
| j |
 задана в прямоугольной системе координат
задана в прямоугольной системе координат 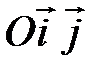 , то
, то  имеет простой геометрический смысл:
имеет простой геометрический смысл: 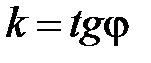 , где
, где 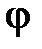 - угол наклона прямой
- угол наклона прямой  к оси
к оси  , т.е. направленный угол
, т.е. направленный угол  (рис. 59).
(рис. 59).
Пусть прямая  задана точкой
задана точкой 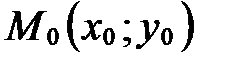 и угловым коэффициентом
и угловым коэффициентом 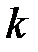 . Запишем каноническое уравнение прямой
. Запишем каноническое уравнение прямой  :
:
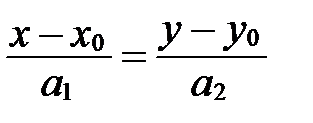
и преобразуем его: 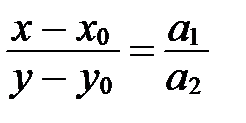 ;
; 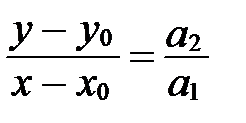 ; учитывая, что
; учитывая, что  , получим:
, получим:
 (16)
(16)
Уравнение (16) называется уравнением прямой, заданной точкой и угловым коэффициентом.
6. Уравнение прямой с угловым коэффициентом.
Пусть 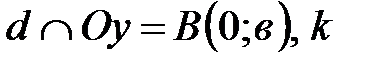 - угловой коэффициент прямой
- угловой коэффициент прямой  . Применяя уравнение (16), получим:
. Применяя уравнение (16), получим: 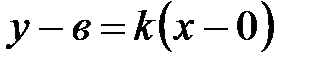 , т.е.
, т.е.
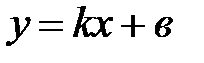 . (17)
. (17)
Уравнение (17) называется уравнением прямой с угловым коэффициентом.
В уравнении (17) в – это ордината точки пересечения прямой  с осью
с осью 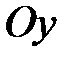 .
.
Основные аффинные задачи,
Лекция 10
Системе координат
Вектором нормали
Ненулевой вектор называется перпендикулярным данной прямой, если он ортогонален любому направляющему вектору этой прямой.
Вектор, перпендикулярный прямой, называется вектором нормали этой прямой или ее нормальным вектором. Для каждой прямой на плоскости существует бесконечное множество векторов нормали. Любые два из них коллинеарны (рис. 61).
Вектор нормали прямой  будем обозначать через
будем обозначать через 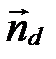 .
.
| Рис. 61 |
| d |
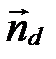
|
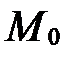
|
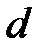
|

|
| Рис. 62 |
Лемма 1. Если прямая  в прямоугольной системе координат
в прямоугольной системе координат 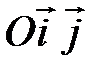 задана уравнением
задана уравнением 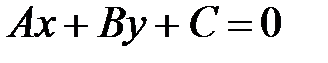 , то вектор
, то вектор 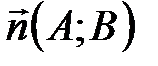 перпендикулярен прямой
перпендикулярен прямой  .
.
□ Возьмем направляющий вектор 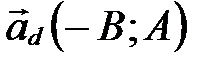 прямой
прямой  и найдем скалярное произведение
и найдем скалярное произведение  . ■
. ■
Следствие. Уравнение прямой  , заданной в прямоугольной декартовой системе координат точкой
, заданной в прямоугольной декартовой системе координат точкой 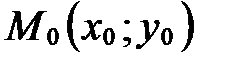 и вектором нормали
и вектором нормали 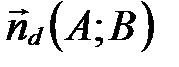 , имеет вид
, имеет вид  .
.
□ Если 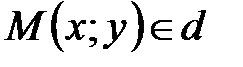 , то
, то 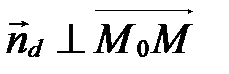 (рис. 62) Þ
(рис. 62) Þ 
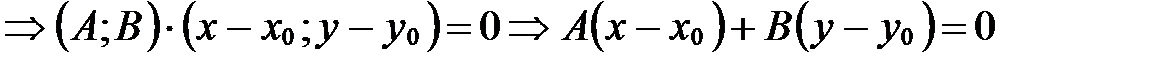 .
.
Если 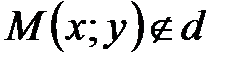 , то вектор
, то вектор 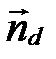 не ортогонален вектору
не ортогонален вектору 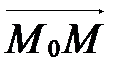 , т.е.
, т.е. 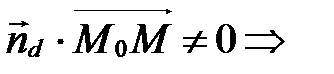
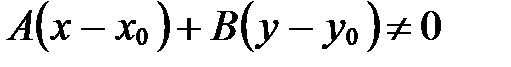 .
.
Итак, доказано, что точка 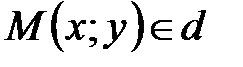 тогда и только тогда, когда ее координаты удовлетворяют уравнению
тогда и только тогда, когда ее координаты удовлетворяют уравнению
 . ■ (19)
. ■ (19)
Уравнение (19) называется уравнением прямой, заданной точкой и вектором нормали.
Замечание. Если в прямоугольной декартовой системе координат прямая  задана общим уравнением
задана общим уравнением 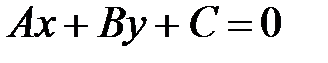 , то геометрический смысл коэффициентов при х и у состоит в следующем: А и В есть координаты вектора нормали прямой
, то геометрический смысл коэффициентов при х и у состоит в следующем: А и В есть координаты вектора нормали прямой  , т.е.
, т.е. 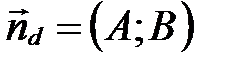 .
.
Элементы векторной алгебры
Векторы. Линейные операции над векторами
Понятие вектора
Направленным отрезком называется отрезок, у которого указаны начало и конец. Обозначение: 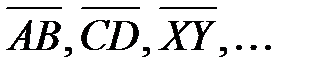
Вектором называется направленный отрезок. Обозначение:  (рис. 1).
(рис. 1).
| А |
| D |
| C |

|
|
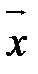
|
| Рис. 1 |
Вектор называется нулевым, если его начало и конец совпадают. Обозначение: 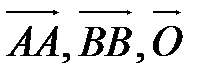 .
.
Векторы  и
и  называются сонаправленными (противоположно направленными), если лучи [ AB ) и [ CD ) сонаправлены (противоположно направлены). Обозначение:
называются сонаправленными (противоположно направленными), если лучи [ AB ) и [ CD ) сонаправлены (противоположно направлены). Обозначение:  (
( 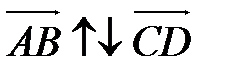 ).
).
На рис. 2  ,
,  .
.
| А |
| В |
| С |
| D |
| K |
| M |
| X |
| Y |
| Рис. 2 |
Векторы 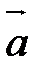 и
и 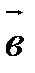 называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Обозначение:
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Обозначение:  ||
|| 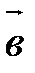 .
.
Нулевой вектор считается коллинеарным любому вектору.
Векторы 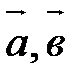 и
и 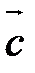 называются компланарными, если существует плоскость, которой они параллельны.
называются компланарными, если существует плоскость, которой они параллельны.
Длиной вектора называется расстояние между его началом и концом. Обозначение длины вектора  :
:  .
.
Длина нулевого вектора равна 0, т.е. 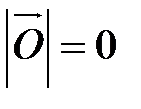 .
.
Вектор называется единичным, если его длина равна единице.
В пространстве существует бесконечное множество единичных векторов.
Два вектора называются равными, если они сонаправлены и длины их равны. Обозначение: 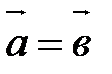 .
.
Два вектора называются противоположными, если они противоположно направлены и длины их равны.
Вектор, противоположный вектору  , обозначается
, обозначается 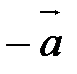 .
.
Откладыванием вектора 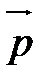 от точки А называется процесс построения такой точки М, что
от точки А называется процесс построения такой точки М, что 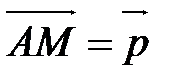 .
.
| В |
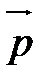 и точка А. Сначала строят луч
и точка А. Сначала строят луч  , исходящий из точки А и сонаправленный с вектором
, исходящий из точки А и сонаправленный с вектором 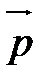 (рис. 3). Затем на луче
(рис. 3). Затем на луче  откладывают с помощью циркуля отрезок АМ, длина которого равна длине вектора
откладывают с помощью циркуля отрезок АМ, длина которого равна длине вектора 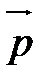 . Вектор
. Вектор 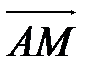 - искомый, т.е.
- искомый, т.е. 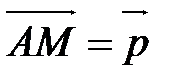 .
.
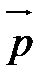
|
| А |
| М |
| Рис. 3 |
§2. Сложение и вычитание векторов
Линейными операциями над векторами называется сложение, вычитание векторов и умножение вектора на число.
Результатом сложения векторов является их сумма. Сумма векторов 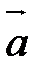 и
и  обозначается
обозначается 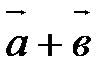 .
.
Существует два правила сложения двух векторов: правило треугольника и правило параллелограмма.
Правило треугольника
Чтобы сложить векторы 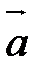 и
и  , надо взять произвольную точку и от нее отложить последовательно сначала вектор
, надо взять произвольную точку и от нее отложить последовательно сначала вектор 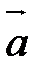 , затем вектор
, затем вектор  . Вектор, начало которого совпадает с началом вектора
. Вектор, начало которого совпадает с началом вектора 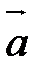 (т.е. первого вектора), а конец – с концом вектора
(т.е. первого вектора), а конец – с концом вектора  (т.е. второго вектора), есть искомая сумма. На рис. 4
(т.е. второго вектора), есть искомая сумма. На рис. 4 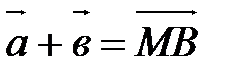 .
.
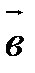
|
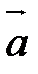
|
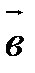
|
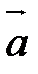
|
| М |
| В |
| Рис. 4 |
По правилу треугольника можно складывать любые векторы.
Коротко правило треугольника можно записать так:
для любых трех точек А,В и С  .
.
Правило параллелограмма
Чтобы сложить векторы 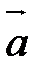 и
и  , надо привести их к общему началу, т.е. взять произвольную точку А, построить такие точки В и С, что
, надо привести их к общему началу, т.е. взять произвольную точку А, построить такие точки В и С, что 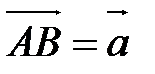 и
и 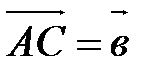 , и достроить полученную фигуру до параллелограмма
, и достроить полученную фигуру до параллелограмма  . Вектор
. Вектор  - искомая сумма (рис. 5).
- искомая сумма (рис. 5).

|

|

|

|
| А |
| С |
| В |
| D |
| Рис. 5 |
По правилу параллелограмма можно складывать тольконеколлинеарные векторы.
Свойства сложения векторов:
10. 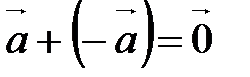
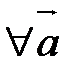 .
.
20. 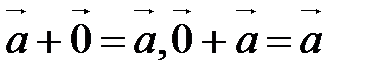
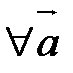 .
.
30. 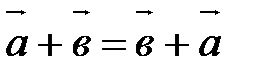
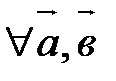 .
.
40. 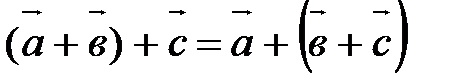
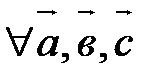 .
.
Суммой трех векторов 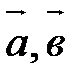 и
и 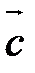 называется вектор
называется вектор 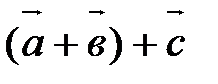 . Учитывая свойство 40, скобки можно опустить и обозначать сумму в виде
. Учитывая свойство 40, скобки можно опустить и обозначать сумму в виде 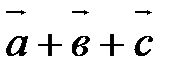 .
.
Суммой n векторов  называется вектор
называется вектор 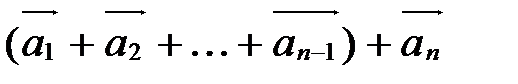 и обозначается так:
и обозначается так: 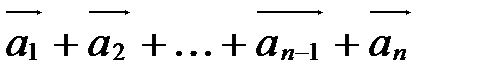 .
.
При построении суммы n векторов пользуются правилом многоугольника.
Правило многоугольника
Чтобы найти сумму n векторов, надо взять произвольную точку и отложить от нее последовательно эти векторы. Вектор, начало которого совпадает с началом первого вектора, а конец – с концом последнего (n-го вектора), есть искомая сумма.
Разностью векторов 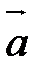 и
и  называется такой вектор
называется такой вектор 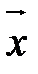 , что
, что  . Разность – это результат вычитания векторов. Разность векторов
. Разность – это результат вычитания векторов. Разность векторов 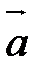 и
и  обозначается так:
обозначается так:  .
.
Дата: 2018-11-18, просмотров: 390.