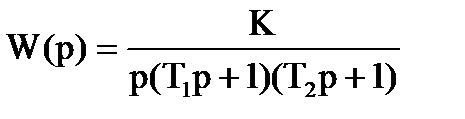Частотный критерий Михайлова формулируется следующим образом:
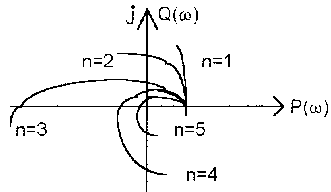
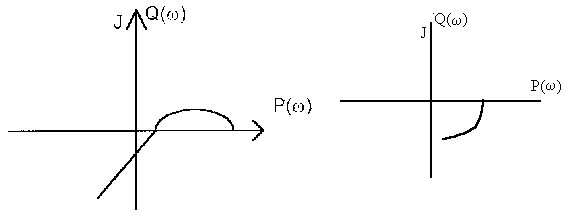
Для устойчивости системы необходимо и достаточно, чтобы годограф Михайлова при изменении частоты w от 0 до ∞, начав движение из точки, лежащий на положительной части вещественной полуоси, вращаясь против часовой стрелки и нигде не обращаясь в 0, прошел последовательно n квадрантов, повернувшись на угол n·p/2, где n – порядок системы.
Система устойчива Неустойчивые системы
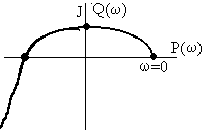
Будем рассматривать системы 3-го порядка, т.е. n=3.
Имеются три характерные точки:
1) w=0
2) P(w)=0
3) Q(w)=0
Если система состоит из последовательно соединенных звеньев: интегрирующего и двух апериодических первого порядка, то передаточная функция разомкнутой системы будет иметь вид 
, а
характеристическое уравнение - M(p)=p(T1p+1)(T2p+1)+K=0
где К – коэффициент усиления
Т – постоянные времени
Раскроем скобки:
T1T2p3+ T1p2+ T2p2+p+K=0
Заменим p на jw:
T1T2j3w3+j2w2(T1+ T2)+jw+K=0
Т.к. j3= - j, а j2= -1, то получим:
-T1T2jw3- w2(T1+ T2)+jw+K=0
Выделим действительные P(w) и мнимые Q(w) части уравнения:
P(w) = - w2(T1+ T2)+K
Q(w) = -T1T2w3+w
Исследуя характерные точки, определим P(w) и Q(w):
1) w=0
P(w=0)=0·(T1+ T2)+K=K
Q(w=0)= -T1T20+0=0
2) P(w)=0
-T1w2-T2w2+K=0
Находим w: w2(T1+T2)=K
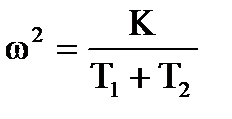
Подставим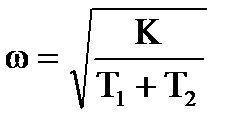 
в Q(w):
3) Q(w)=0
-T1T2w3+w=0
Находим w: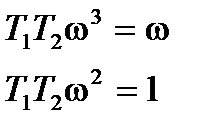 
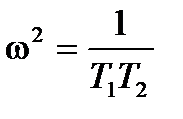
Подставим 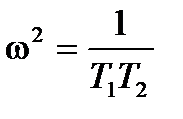в P(w):
Отложим на графике полученные точки и кривая, проходящая через них будет годографом Михайлова:
Система устойчива т.к. годограф Михайлова проходит последовательно три квадранта против часовой стрелки и нигде не обращается в нуль.
Пример расчета
Исходные данные:
Передаточная функция разомкнутой системы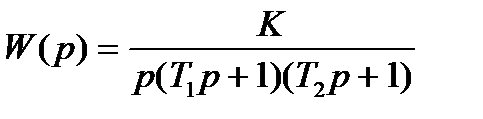 
, где T1=0,57с ; T2=0,01с; K=58
Решение:
M(p)=p(T1p+1)(T2p+1)+K=0
0,0057p3+ 0,57p2+ 0,01p2+p+58=0
Заменим p на jw:
0,0057(jw)3+ 0,57(jw)2+ 0,01(jw)2+(jw)+58=0
-0,0057jw3-0,57w2-0,01w2+jw+58=0
Выделим действительные и мнимые части и обозначим P(w) и Q(w):
P(w) = -0,57w2-0,01w2+58
Q(w) = -0,0057w3+w
Исследуем характерные точки и определим P(w) и Q(w):
1. w=0
P( w)=58
Q(w)=0
2. P(w)=0
-0,57w2-0,01w2+58=0
-0,58w2= -58
w2=100, w=10
Q(w) = -0,0057×103+10=4,3
Q( w) =4,3
3. Q(w)=0
-0,0057w3+w=0
-0,0057w2+1=0
w2=175, w=13
P(w) = -0,57×175-0,01×175+58= -41,5
P( w) =-41,5
Построим годограф Михайлова:
Данная система устойчива, т.к. годограф последовательно проходит через три квадранта против часовой стрелки и нигде не обращается в нуль.
Задание:
1. Определить устойчивость системы с помощью критерия Михайлова по известной передаточной функции. Исходные данные для расчета взять из таблицы 1, согласно варианту:
Таблица 1
| № варианта | Передаточная функция | Т1, с | Т2, с | К |
| 1 |
| 0,56 | 0,01 | 57 |
| 2 | 1 | 0,02 | 55 | |
| 3 | 0,44 | 0,01 | 45 | |
| 4 | 0,87 | 0,02 | 43 | |
| 5 | 0,18 | 0,01 | 19 |
2. Произвести расчет:
М(р)=____________________________________________________________
М(jw)=___________________________________________________________
P(w)=_____________________________________________________________
Q(w)=____________________________________________________________
1) точка при (w=0):
P(w=0)=__________________________________________________________
Q(w=0)=__________________________________________________________
2) точка при P(w)=0:
_________________________________________________________
w=_______________________________________________________________
Q(w)=____________________________________________________________
4) точка при Q(w)=0:
_________________________________________________________________
w=_______________________________________________________________
P(w)=_____________________________________________________________
3. Построить годограф Михайлова и определить, устойчива ли система.
4. Составить программы определения величин P(w) и Q(w) на языке программирования высокого уровня
5. Вычислить на компьютере величины P(w) и Q(w)
6. Построить годограф Михайлова, используя пакет прикладных программ «Компас»
Контрольные вопросы:
1.Критерий устойчивости Михайлова частотный или алгебраический?
2.Сколько квадрантов должен пройти годограф Михайлова, описывающий устойчивую систему четвертого порядка?
3. Приведите характерные точки для построения годографа Михайлова третьего порядка?
4. Будет ли система устойчива, если годограф ее описывающий, пойдет по часовой стрелке?
Лабораторная работа № 8
«Определение с помощью критерия Михайлова коэффициента передачи (К), при котором система находится на границе устойчивости»
Цель работы
Определить при каком коэффициенте передачи (К) система будет находиться на границе устойчивости.
Образовательные результаты, заявленные во ФГОС третьего поколения
Студент должен
уметь:
- решать задачи операторным методом;
- определять передаточные функции звеньев и систем автоматического управления (САУ);
- строить частотные характеристики звеньев и систем автоматического управления;
- исследовать устойчивость и качественные показатели систем автоматического управления.
знать:
- типовые динамические звенья САУ, их соединения в системы, передаточные функции и амплитудо-фазо-частотные (АФЧХ) и логарифмические амплитудо-фазо-частотные характеристики (ЛАХ) и (ЛФХ) звеньев и систем;
- критерии устойчивости систем: Рауса-Гурвица, Михайлова, Найквиста и логарифмический;
Дата: 2018-11-18, просмотров: 306.
