Определение устойчивости системы используя критерий Рауса - Гурвица.
1) Для систем, имеющих характеристические уравнения 1 - го порядка:
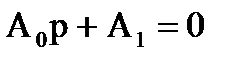
необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были положительными, т. е. 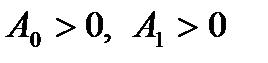
2) Для систем, имеющих характеристические уравнения 2 - го порядка:
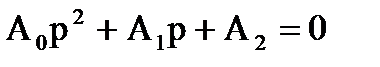
необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были положительными, т.е. 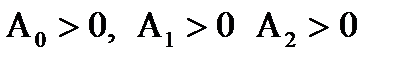
3) Для систем, имеющих характеристические уравнения 3 - го порядка
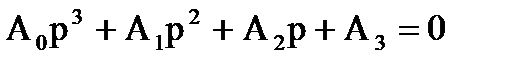
необходимо и достаточно, что6ы все коэффициенты характеристического уравнения, а также определитель 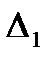 были положительными, т.е
были положительными, т.е
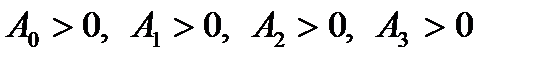
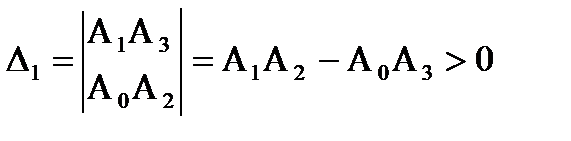
4) Для систем, имеющих характеристические уравнения 4-го порядка
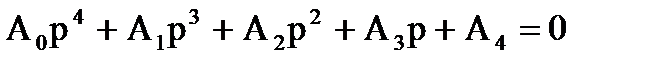
необходимо и достаточно, что6ы все коэффициенты характеристического уравнения, а также определители 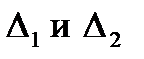 , были положительными, т.е.
, были положительными, т.е.
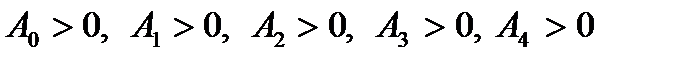
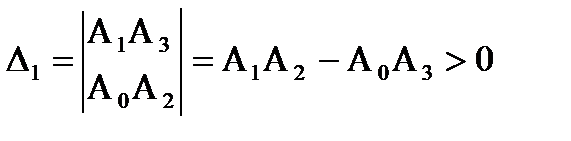
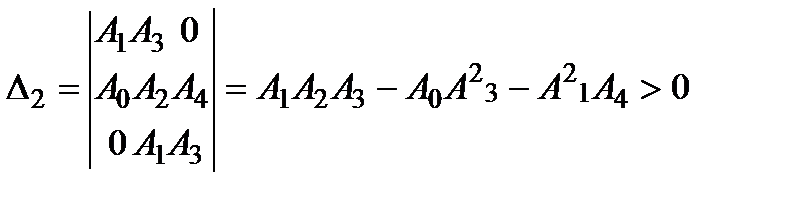
Пример расчёта
Исходные данные:
Характеристическое уравнение системы 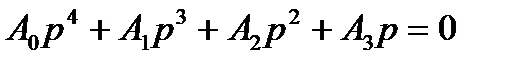 , где A0=0,1; А1=2,3; А3=50; А4=200
, где A0=0,1; А1=2,3; А3=50; А4=200
Решение:
1) 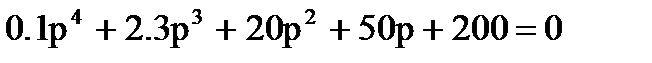
2) 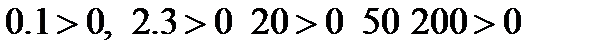
3) 
4)  2,3·20·50-0,1·50·50-2,3·200·2,3=2300-250-1058= 992>0
2,3·20·50-0,1·50·50-2,3·200·2,3=2300-250-1058= 992>0
Система устойчива, т.к. коэффициенты А0, А1, А2, А3 и определители D1 и D2 больше нуля.
Задание:
1. Определить устойчива ли система, заданная характеристическим уравнением 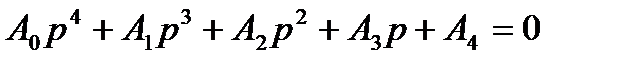 . Исходные данные для расчета взять из таблицы 1, согласно варианту
. Исходные данные для расчета взять из таблицы 1, согласно варианту
Таблица 1.
| № варианта | А0 | А1 | А2 | А3 | А4 |
| 1 | 0,1 | 2,5 | 20 | 50 | 200 |
| 2 | 0,5 | 3 | 35 | 60 | 250 |
| 3 | 0,1 | 2 | 10 | 25 | 100 |
| 4 | 0,3 | 1,5 | 15 | 55 | 150 |
| 5 | 0,2 | 35 | 25 | 40 | 300 |
2. Произвести расчет:
А0______________________________________________________________
А1_______________________________________________________________
А2_______________________________________________________________
А3_______________________________________________________________
А4_______________________________________________________________
∆1=
______________________________________________________________
∆2=
______________________________________________________________
3. Сделать вывод устойчива ли система
4. Составить программу определения величины ∆1 (∆2) на языке программирования высокого уровня
5. Вычислить на компьютере величину ∆1 (∆2) и сравнить с расчетной
Контрольные вопросы:
1.Критерий устойчивости Рауса - Гурвица частотный или алгебраический?
2.Для определения устойчивости систем какого порядка не надо считать определители?
3. Для системы третьего порядка достаточно ли иметь только положительными все коэффициенты характеристического уравнения?
4. Как определить устойчива ли система четвертого порядка?
Лабораторная работа № 6,7
«Определение устойчивости системы с помощью критерия Михайлова»
Цель работы
Научиться определять устойчивость системы, используя критерий Михайлова
Образовательные результаты, заявленные во ФГОС третьего поколения:
Студент должен
уметь:
- решать задачи операторным методом;
- определять передаточные функции звеньев и систем автоматического управления (САУ);
- строить частотные характеристики звеньев и систем автоматического управления;
- исследовать устойчивость и качественные показатели систем автоматического управления.
знать:
- типовые динамические звенья САУ, их соединения в системы, передаточные функции и амплитудо-фазо-частотные (АФЧХ) и логарифмические амплитудо-фазо-частотные характеристики (ЛАХ) и (ЛФХ) звеньев и систем;
- критерии устойчивости систем: Рауса-Гурвица, Михайлова, Найквиста и логарифмический;
Дата: 2018-11-18, просмотров: 375.