УФИМСКИЙ ГОСУДАРСТВЕННЫЙ КОЛЛЕДЖ РАДИОЭЛЕКТРОНИКИ,
ТЕЛЕКОММУНИКАЦИИ и БЕЗОПАСНОСТИ
РАБОЧАЯ ТЕТРАДЬ
ДИСЦИПЛИНА «ОСНОВЫ СИСТЕМ УПРАВЛЕНИЯ»
Вариант №
Выполнил студент___________________
Группы_________
Проверил преподаватель __________Фридман Г.М.
Оценка: ______________
Уфа 2015
Лабораторная работа № 1
«Решение задач операторным методом»
Цель работы: Исследовать возможности операторного метода при решении дифференциальных уравнений, описывающих работу системы.
Образовательные результаты, заявленные во ФГОС третьего поколения:
Студент должен
уметь:
- решать задачи операторным методом;
знать:
- типовые динамические звенья САУ, их соединения в системы, передаточные функции и амплитудо-фазо-частотные (АФЧХ) и логарифмические амплитудо-фазо-частотные характеристики (ЛАХ) и (ЛФХ) звеньев и систем;
-
Краткие теоретические и учебно-методические материалы по теме лабораторной работы
Операторная форма записи дифференциальных уравнений – это такая их своеобразная форма записи, когда операции дифференцирования и интегрирования заменяют алгебраическими операциями над числом Р.
При решении дифференциальных уравнений операторным методом переходят от данных функций, называемых оригиналами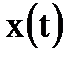 
, к их изображениям 
; совершают более простые действия над полученными изображениями, а затем полученный результат в виде изображения переводят в оригинал, т.е. по найденному изображению находят оригинал.
На практике переход от оригиналов к изображениям и обратно осуществляется по таблицам типовых функций (таблица 1).
Таблица 1
| Оригинал | А |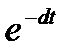 
| 
| 
| 
|
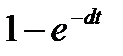
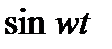
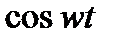
| Изображение | А | 
| 
| 
| 
|
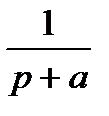
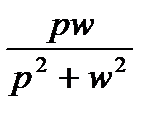
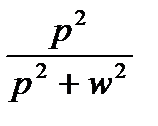
Пример расчета
Исходные данные:
RC цепь (рис. 1), дифференциальное уравнение описывающее работу цепи, Uвх=220 В, R=100 Ом, C=100 мФ.
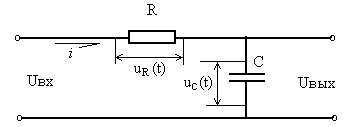
Рисунок 1
Решение
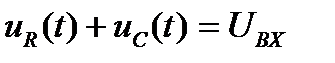
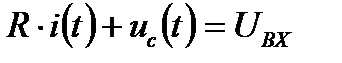
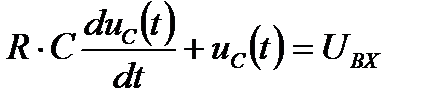
Заменим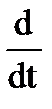 
на р и получим изображение:
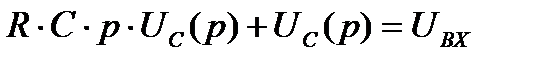
Вынесем Uс(p) за скобки:
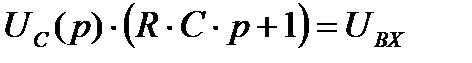
Найдем Uc(p):
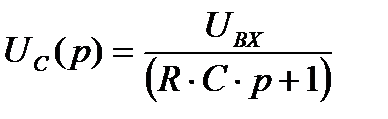
Чтобы воспользоваться таблицей и перейти от изображения к
оригиналу необходимо свести данное выражение к табличному, для этого поделим числитель и знаменатель на RC и получим:
.
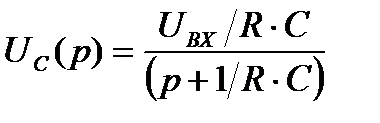1/RC есть а, тогда
.
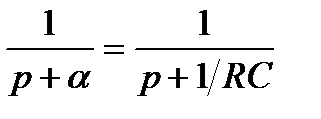Изображение 
соответствует оригиналу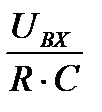 
, а изображение
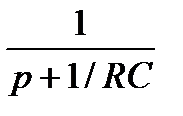- оригиналу 
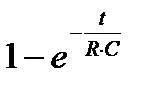, т.е. получаем
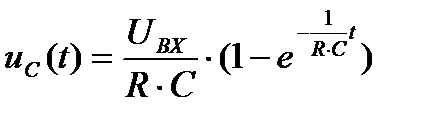
=22*(1 – е0,1*t)
Задание:
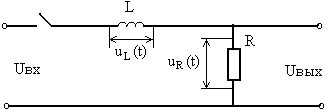
1. Используя операторный метод решить дифференциальное уравнение, описывающее RL цепь (рис. 2) относительно тока i(t), т.е. найти i(t). Исходные данные для расчета взять из таблицы 2,согласно варианту.
Рисунок 2
Таблица 2.
| № варианта | Дифференциальное уравнение | Uвх, В | R, Ом | L, Гн |
| 1 |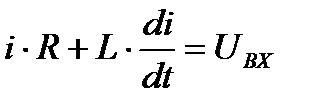 
| 220 | 100 | 100 |
| 2 |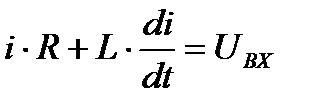
| 380 | 200 | 150 |
| 3 |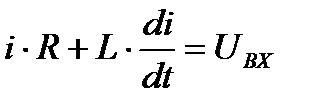
| 220 | 300 | 300 |
| 4 |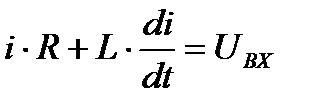
| 380 | 500 | 400 |
| 5 |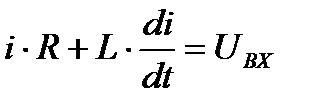
| 220 | 800 | 800 |
2. Произвести расчет:
Uвх (при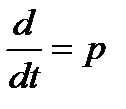 
)= _______________________________________________________
__________________________________________________________________________
I(p)=________________________________________________________________________
_____________________________________________________________________________
i(t)=_________________________________________________________________________
______________________________________________________________________
3. Составить программу определения постоянной величины на языке программирования высокого уровня
4. Вычислить на компьютере постоянную величину и сравнить с расчетной
Контрольные вопросы:
1. Какие операции заменяют алгебраическими операциями над числом Р при операторной форме записи дифференциальных уравнений?
2. Какие функции являются оригиналами?
3. Какие функции являются изображениями?
4. Над какими из функций оригиналами или изображениями совершают простые действия при решении дифференциальных уравнений операторным методом?
Лабораторная работа №2
«Определение передаточных функций разомкнутой и замкнутой систем»
Цель работы
Научиться определять передаточные функции систем.
Образовательные результаты, заявленные во ФГОС третьего поколения:
Студент должен
уметь:
- решать задачи операторным методом;
- определять передаточные функции звеньев и систем автоматического управления (САУ);
знать:
- типовые динамические звенья САУ, их соединения в системы, передаточные функции и амплитудо-фазо-частотные (АФЧХ) и логарифмические амплитудо-фазо-частотные характеристики (ЛАХ) и (ЛФХ) звеньев и систем;
Пример расчета
Исходные данные:
Решение
1. 
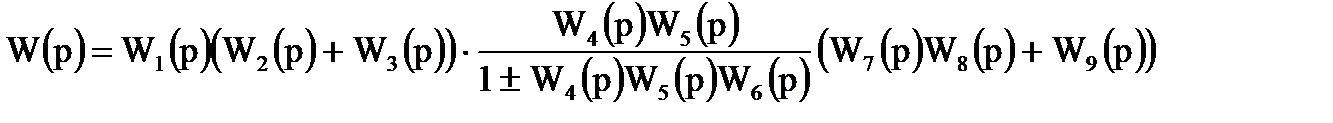
2. 
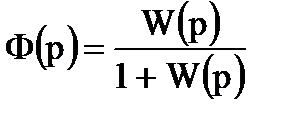
Задание:
1. Определить передаточную функцию замкнутой системы. Исходные данные для расчета взять из таблицы 1, согласно варианту.
Таблица 1
| № варианта | Замкнутая САР |
| 1 |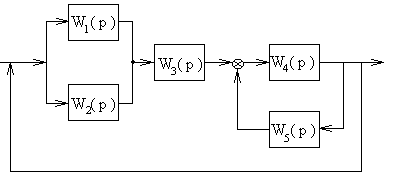 
|
| 2 |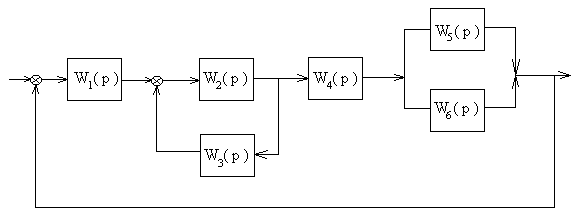 
|
| 3 |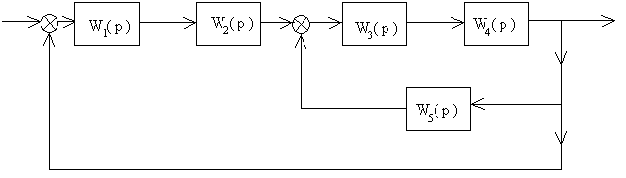 
|
| 4 |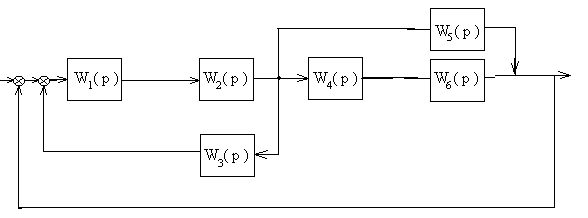 
|
| 5 |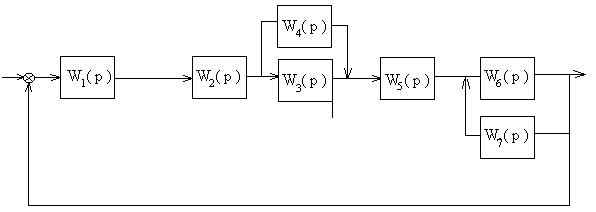 
|
2. Произвести расчет:
W(p)=___________________________________________________________
______________________________________________________________
Ф(р)=____________________________________________________________
Контрольные вопросы:
1. Как определяется передаточная функция разомкнутой системы?
2. Чему равна передаточная функция разомкнутой системы, состоящей из последовательно соединенных звеньев?
3. Чему равна передаточная функция разомкнутой системы, состоящей из параллельно соединенных звеньев?
4. Чему равна передаточная функция замкнутой системы?
Лабораторная работа №3,4
«Построение АФЧХ статической разомкнутой системы»
Цель работы
Научиться строить АФЧХ разомкнутой САР по передаточной функции.
Образовательные результаты, заявленные во ФГОС третьего поколения:
Студент должен
уметь:
- решать задачи операторным методом;
- определять передаточные функции звеньев и систем автоматического управления (САУ);
- строить частотные характеристики звеньев и систем автоматического управления;
знать:
- типовые динамические звенья САУ, их соединения в системы, передаточные функции и амплитудо-фазо-частотные (АФЧХ) и логарифмические амплитудо-фазо-частотные характеристики (ЛАХ) и (ЛФХ) звеньев и систем;
Пример расчета
Построить АФЧХ вычислив A(w) и j(w), (задаваясь десятью значениями частоты w от нуля до ∞) если передаточная функция разомкнутой системы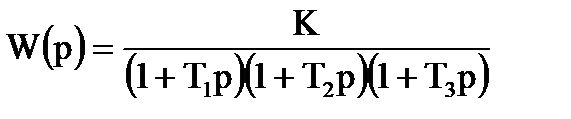 
, в которой Т1=0,2с; Т2=0,3с; Т3=0,4с; К=10.
Решение:
1) 
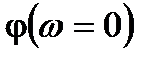=10
=0
2) 
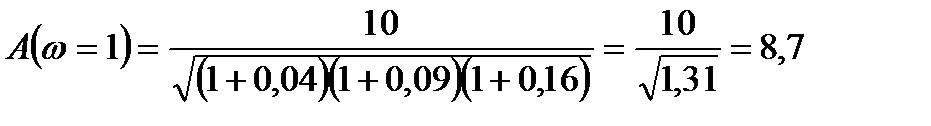
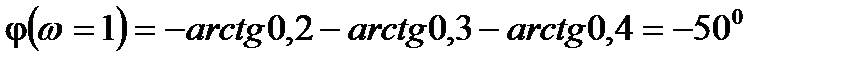
3) 
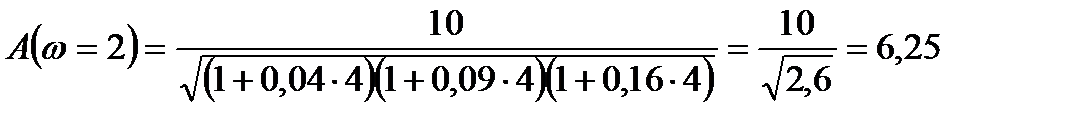
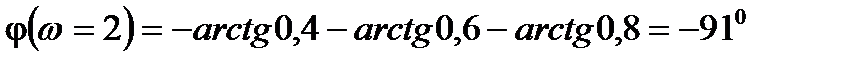
4) 
5) 
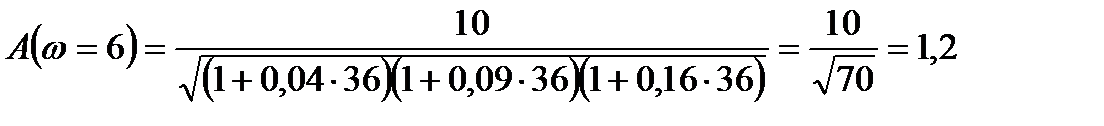
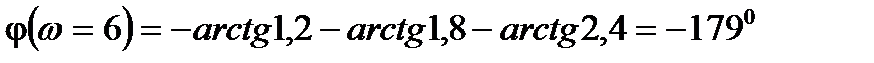
6) 
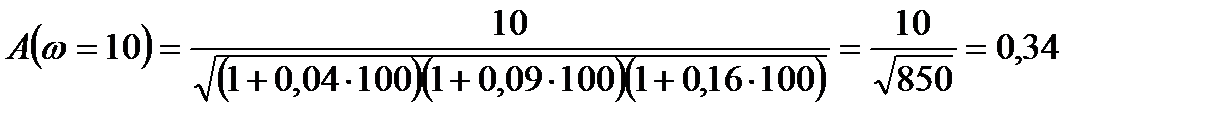
7) 
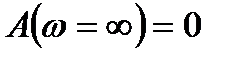
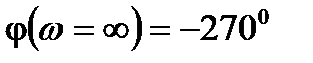
Построим по полученным точкам график:
J
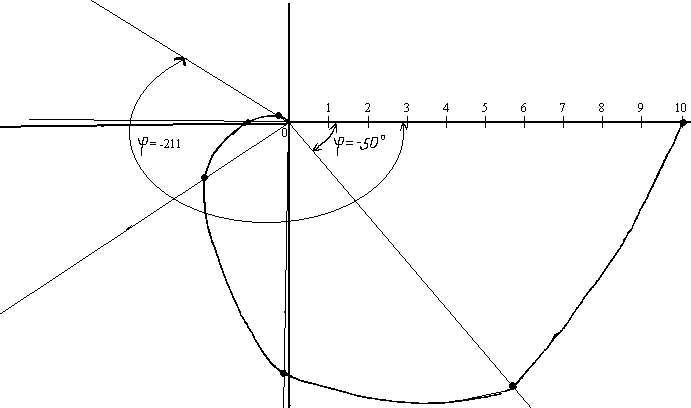
Задание:
1. Для передаточной функции системы 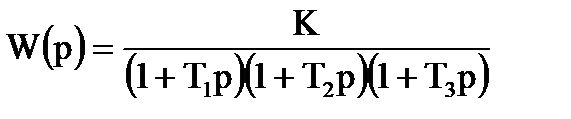построить АФЧХ. Исходные данные для расчета взять из таблицы 1, согласно варианту.
Таблица 1
| № варианта | К | 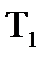 ,с
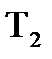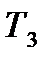|  ,с
|  ,с
|
| 1 | 14 | 0,02 | 0,3 | 0,4 |
| 2 | 10 | 0,03 | 0,3 | 0,5 |
| 3 | 20 | 0,02 | 0,2 | 0,2 |
| 4 | 20 | 0,02 | 0,2 | 0,3 |
| 5 | 15 | 0,03 | 0,2 | 0,6 |
2. Произвести расчет 
и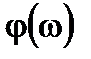 
(десять точек)
3. По полученным данным построить АФЧХ на "миллиметровке".
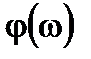4. Составить программы определения и на языке программирования высокого уровня
5. Вычислить на компьютере по 10 точек значений и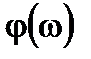
6. Построить АФЧХ, используя пакет прикладных программ «Компас»
Контрольные вопросы:
1. Что называется АФЧХ линейной САР?
2.Как получить АФЧХ, зная передаточную функцию разомкнутой системы?
3.Что такое годограф?
4. Как построить годограф?
Лабораторная работа № 5
«Определение устойчивости системы с помощью критерия Рауса – Гурвица»
Цель работы
Научиться определять устойчивость САР с помощью критерия Рауса-Гурвица.
Образовательные результаты, заявленные во ФГОС третьего поколения:
Студент должен
уметь:
- решать задачи операторным методом;
- определять передаточные функции звеньев и систем автоматического управления (САУ);
- строить частотные характеристики звеньев и систем автоматического управления;
- исследовать устойчивость и качественные показатели систем автоматического управления.
знать:
- типовые динамические звенья САУ, их соединения в системы, передаточные функции и амплитудо-фазо-частотные (АФЧХ) и логарифмические амплитудо-фазо-частотные характеристики (ЛАХ) и (ЛФХ) звеньев и систем;
- критерии устойчивости систем: Рауса-Гурвица, Михайлова, Найквиста и логарифмический;
Пример расчёта
Исходные данные:
Характеристическое уравнение системы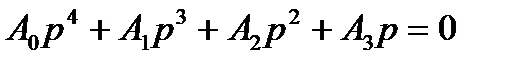 
, где A0=0,1; А1=2,3; А3=50; А4=200
Решение:
1) 
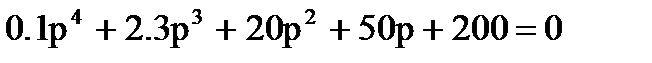
2) 
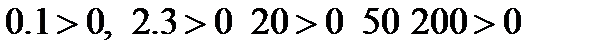
3) 
4) 
2,3·20·50-0,1·50·50-2,3·200·2,3=2300-250-1058= 992>0
Система устойчива, т.к. коэффициенты А0, А1, А2, А3 и определители D1 и D2 больше нуля.
Задание:
1. Определить устойчива ли система, заданная характеристическим уравнением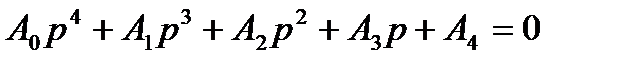 
. Исходные данные для расчета взять из таблицы 1, согласно варианту
Таблица 1.
| № варианта | А0 | А1 | А2 | А3 | А4 |
| 1 | 0,1 | 2,5 | 20 | 50 | 200 |
| 2 | 0,5 | 3 | 35 | 60 | 250 |
| 3 | 0,1 | 2 | 10 | 25 | 100 |
| 4 | 0,3 | 1,5 | 15 | 55 | 150 |
| 5 | 0,2 | 35 | 25 | 40 | 300 |
2. Произвести расчет:
А0______________________________________________________________
А1_______________________________________________________________
А2_______________________________________________________________
А3_______________________________________________________________
А4_______________________________________________________________
∆1=
______________________________________________________________
∆2=
______________________________________________________________
3. Сделать вывод устойчива ли система
4. Составить программу определения величины ∆1 (∆2) на языке программирования высокого уровня
5. Вычислить на компьютере величину ∆1 (∆2) и сравнить с расчетной
Контрольные вопросы:
1.Критерий устойчивости Рауса - Гурвица частотный или алгебраический?
2.Для определения устойчивости систем какого порядка не надо считать определители?
3. Для системы третьего порядка достаточно ли иметь только положительными все коэффициенты характеристического уравнения?
4. Как определить устойчива ли система четвертого порядка?
Лабораторная работа № 6,7
«Определение устойчивости системы с помощью критерия Михайлова»
Цель работы
Научиться определять устойчивость системы, используя критерий Михайлова
Образовательные результаты, заявленные во ФГОС третьего поколения:
Студент должен
уметь:
- решать задачи операторным методом;
- определять передаточные функции звеньев и систем автоматического управления (САУ);
- строить частотные характеристики звеньев и систем автоматического управления;
- исследовать устойчивость и качественные показатели систем автоматического управления.
знать:
- типовые динамические звенья САУ, их соединения в системы, передаточные функции и амплитудо-фазо-частотные (АФЧХ) и логарифмические амплитудо-фазо-частотные характеристики (ЛАХ) и (ЛФХ) звеньев и систем;
- критерии устойчивости систем: Рауса-Гурвица, Михайлова, Найквиста и логарифмический;
Пример расчета
Исходные данные:
Передаточная функция разомкнутой системы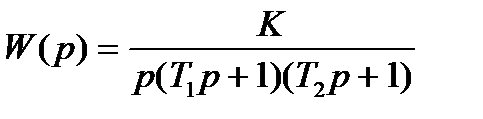 
, где T1=0,57с ; T2=0,01с; K=58
Решение:
M(p)=p(T1p+1)(T2p+1)+K=0
0,0057p3+ 0,57p2+ 0,01p2+p+58=0
Заменим p на jw:
0,0057(jw)3+ 0,57(jw)2+ 0,01(jw)2+(jw)+58=0
-0,0057jw3-0,57w2-0,01w2+jw+58=0
Выделим действительные и мнимые части и обозначим P(w) и Q(w):
P(w) = -0,57w2-0,01w2+58
Q(w) = -0,0057w3+w
Исследуем характерные точки и определим P(w) и Q(w):
1. w=0
P( w)=58
Q(w)=0
2. P(w)=0
-0,57w2-0,01w2+58=0
-0,58w2= -58
w2=100, w=10
Q(w) = -0,0057×103+10=4,3
Q( w) =4,3
3. Q(w)=0
-0,0057w3+w=0
-0,0057w2+1=0
w2=175, w=13
P(w) = -0,57×175-0,01×175+58= -41,5
P( w) =-41,5
Построим годограф Михайлова:
Данная система устойчива, т.к. годограф последовательно проходит через три квадранта против часовой стрелки и нигде не обращается в нуль.
Задание:
1. Определить устойчивость системы с помощью критерия Михайлова по известной передаточной функции. Исходные данные для расчета взять из таблицы 1, согласно варианту:
Таблица 1
| № варианта | Передаточная функция | Т1, с | Т2, с | К |
| 1 |
| 0,56 | 0,01 | 57 |
| 2 | 1 | 0,02 | 55 | |
| 3 | 0,44 | 0,01 | 45 | |
| 4 | 0,87 | 0,02 | 43 | |
| 5 | 0,18 | 0,01 | 19 |
2. Произвести расчет:
М(р)=____________________________________________________________
М(jw)=___________________________________________________________
P(w)=_____________________________________________________________
Q(w)=____________________________________________________________
1) точка при (w=0):
P(w=0)=__________________________________________________________
Q(w=0)=__________________________________________________________
2) точка при P(w)=0:
_________________________________________________________
w=_______________________________________________________________
Q(w)=____________________________________________________________
4) точка при Q(w)=0:
_________________________________________________________________
w=_______________________________________________________________
P(w)=_____________________________________________________________
3. Построить годограф Михайлова и определить, устойчива ли система.
4. Составить программы определения величин P(w) и Q(w) на языке программирования высокого уровня
5. Вычислить на компьютере величины P(w) и Q(w)
6. Построить годограф Михайлова, используя пакет прикладных программ «Компас»
Контрольные вопросы:
1.Критерий устойчивости Михайлова частотный или алгебраический?
2.Сколько квадрантов должен пройти годограф Михайлова, описывающий устойчивую систему четвертого порядка?
3. Приведите характерные точки для построения годографа Михайлова третьего порядка?
4. Будет ли система устойчива, если годограф ее описывающий, пойдет по часовой стрелке?
Лабораторная работа № 8
«Определение с помощью критерия Михайлова коэффициента передачи (К), при котором система находится на границе устойчивости»
Цель работы
Определить при каком коэффициенте передачи (К) система будет находиться на границе устойчивости.
Образовательные результаты, заявленные во ФГОС третьего поколения
Студент должен
уметь:
- решать задачи операторным методом;
- определять передаточные функции звеньев и систем автоматического управления (САУ);
- строить частотные характеристики звеньев и систем автоматического управления;
- исследовать устойчивость и качественные показатели систем автоматического управления.
знать:
- типовые динамические звенья САУ, их соединения в системы, передаточные функции и амплитудо-фазо-частотные (АФЧХ) и логарифмические амплитудо-фазо-частотные характеристики (ЛАХ) и (ЛФХ) звеньев и систем;
- критерии устойчивости систем: Рауса-Гурвица, Михайлова, Найквиста и логарифмический;
Пример расчета
Исходные данные:
Передаточная система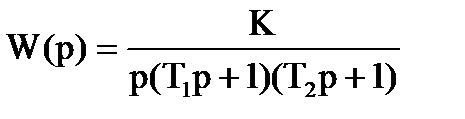 
, где T1= 0,5 с; T2=0,1 с.
Решение:
Характеристическое уравнение M(p):
M(p)=p(T1p+1)(T2p+1)+K=0
T1T2p3+ T1p2+ T2p2+p+K=0
0,05p3+ 0,5p2+ 0,1p2+p+K=0
Заменим p на jw:
M(jw)=0,05 (jw)3+ 0,5(jw)2+ 0,1(jw)2+(jw)+K=0
-0,05 jw3-0,6w2+jw+K=0
Выделим действительную и мнимую части
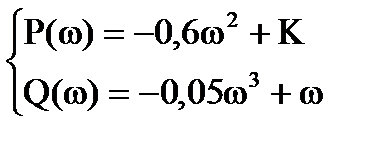
Найдем w из Q(w) и подставим в P(w)
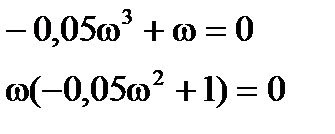
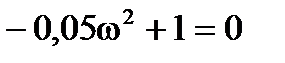
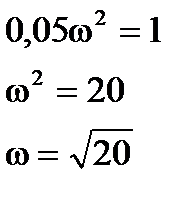
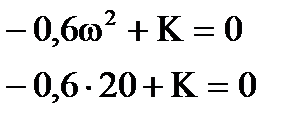
Система будет находиться на границе устойчивости при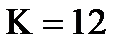 
Задание:
1. Определить при каком K система будет находиться на границе устойчивости, если известна передаточная функция разомкнутой системы. Исходные данные взять из таблицы 1, согласно варианту:
Таблица 1
| № варианта | Передаточная функция | Т1, с | Т2, с |
| 1 |
| 0,5 | 0,2 |
| 2 | 0,3 | 0,2 | |
| 3 | 0,7 | 0,1 | |
| 4 | 0,6 | 0,2 | |
| 5 | 0,4 | 0,1 |
2. Произвести расчет:
М(р)=____________________________________________________________
М(jw)=___________________________________________________________
P(w)=_____________________________________________________________
Q(w)=____________________________________________________________
w=_______________________________________________________________
_________________________________________________________________
K=_______________________________________________________________
3. Составить программу решения системы уравнения с целью определения величины К, при котором система находится на границе устойчивости на языке программирования высокого уровня
4. Вычислить на компьютере величину К
Контрольные вопросы:
1.К каким критериям устойчивости относится критерий Михайлова?
2. Годограф Михайлова строится для разомкнутой или для замкнутой системы?
3. Приведите характерные точки для системы, находящейся на границе устойчивости?
4. Может ли коэффициент К, при котором система находится на границе устойчивости, быть отрицательным?
Лабораторная работа №9,10
«Определение устойчивости и запасов устойчивости системы по амплитуде и фазе с помощью критерия Найквиста»
Цель работы
Научиться определять, устойчива ли система, используя критерий Найквиста
Образовательные результаты, заявленные во ФГОС третьего поколения:
Студент должен
уметь:
- решать задачи операторным методом;
- определять передаточные функции звеньев и систем автоматического управления (САУ);
- строить частотные характеристики звеньев и систем автоматического управления;
- исследовать устойчивость и качественные показатели систем автоматического управления.
знать:
- типовые динамические звенья САУ, их соединения в системы, передаточные функции и амплитудо-фазо-частотные (АФЧХ) и логарифмические амплитудо-фазо-частотные характеристики (ЛАХ) и (ЛФХ) звеньев и систем;
- критерии устойчивости систем: Рауса-Гурвица, Михайлова, Найквиста и логарифмический
Пример расчета
Исходные данные:
Передаточная функция разомкнутой системы
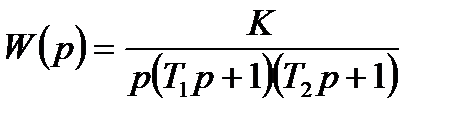, где
Решение:
Для построения АФЧХ разомкнутой системы определим A(w) и j(w):
,
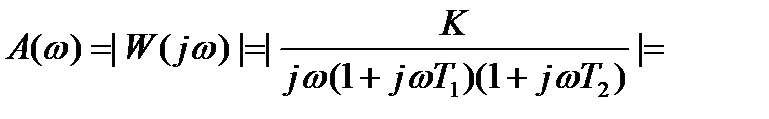
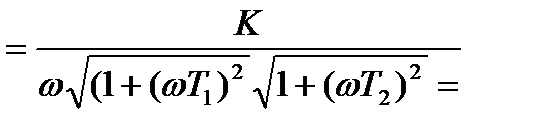
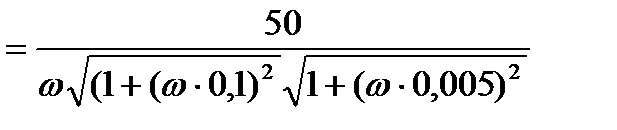, где
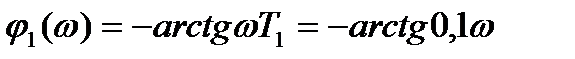
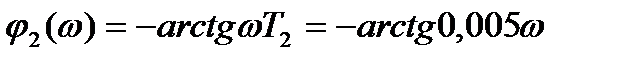
Вычислим А(w), j1(w), j2(w), j(w) для ряда значений w от 0 до ¥ по указанным выше формулам.
Результаты расчета сведем в таблицу 1.
Таблица 1
| w | 0 | 5 | 10 | 15 | 25 | 50 |
| А | ¥ | 9 | 4 | 2 | 0,7 | 0,03 |
| j1(w) | 0 | -26 | -45 | -56 | -68 | -79 |
| j2(w) | 0 | -1 | -3 | -4 | -7 | -14 |
| j(w) | -90 | -117 | -138 | -150 | -165 | -183 |
J
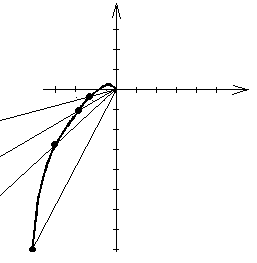
Задание:
1. Построить АФЧХ системы, произведя расчет при изменении частоты от 0 до ¥ (10 значений) и определить устойчивость, используя критерий Найквиста. Исходные данные для расчета и построения взять из таблицы 2, согласно варианту.
Таблица 2
| № варианта | K | T1, с | T2, с |
| 1 | 50 | 0,1 | 0,004 |
| 2 | 45 | 0,1 | 0,003 |
| 3 | 40 | 0,14 | 0,005 |
| 4 | 55 | 0,1 | 0,003 |
| 5 | 50 | 0,1 | 0,002 |
2. Произвести расчет:
W(p)=____________________________________________________________
W(jw)=___________________________________________________________
Ai(w)=________________________________________________________________________
ji(w)=____________________________________________________________________
3. По полученным данным построить АФЧХ на "миллиметровке" и определить запасы устойчивости по амплитуде и фазе
4. Составить программы определения величин А(w) и j(w) на языке программирования высокого уровня
5. Вычислить на компьютере величины А(w) и j(w) (10 значений)
6. Построить АФЧХ, используя пакет прикладных программ «Компас» и определить запасы устойчивости по амплитуде и фазе
Контрольные вопросы:
1.К каким критериям устойчивости относится критерий Найквиста?
2. Можно ли по виду АФЧХ разомкнутой системы судить об устойчивости системы в замкнутом состоянии?
3.Замкнутая система является устойчивой, если АФЧХ W(jw) не охватывает точку с координатами (-1;j0) или если охватывает эту точку?
4. Можно ли судить об устойчивости замкнутой системы по АФЧХ разомкнутой системы, если характеристика W(jw) проходит через точку (-1;j0)
Лабораторная работа № 11,12
«Определение устойчивости и запасов устойчивости системыпо амплитуде и фазе с помощью логарифмического критерия»
Цель работы
Научиться определять устойчивость САР по логарифмическим частотным характеристикам.
Образовательные результаты, заявленные во ФГОС третьего поколения:
Студент должен
уметь:
- решать задачи операторным методом;
- определять передаточные функции звеньев и систем автоматического управления (САУ);
- строить частотные характеристики звеньев и систем автоматического управления;
- исследовать устойчивость и качественные показатели систем автоматического управления.
знать:
- типовые динамические звенья САУ, их соединения в системы, передаточные функции и амплитудо-фазо-частотные (АФЧХ) и логарифмические амплитудо-фазо-частотные характеристики (ЛАХ) и (ЛФХ) звеньев и систем;
- критерии устойчивости систем: Рауса-Гурвица, Михайлова, Найквиста и логарифмический;
Цель работы
Ознакомиться с изменениями, происходящими в звеньях при введении корректирующих устройств.
Образовательные результаты, заявленные во ФГОС третьего поколения:
Студент должен
уметь:
- решать задачи операторным методом;
- определять передаточные функции звеньев и систем автоматического управления (САУ);
- строить частотные характеристики звеньев и систем автоматического управления;
- исследовать устойчивость и качественные показатели систем автоматического управления.
знать:
- типовые динамические звенья САУ, их соединения в системы, передаточные функции и амплитудо-фазо-частотные (АФЧХ) и логарифмические амплитудо-фазо-частотные характеристики (ЛАХ) и (ЛФХ) звеньев и систем;
- критерии устойчивости систем: Рауса-Гурвица, Михайлова, Найквиста и логарифмический;
- качественные показатели САУ.
Пример расчета
Исходные данные:
1) Апериодическое звено1 - го порядка охвачено жесткой ОС.
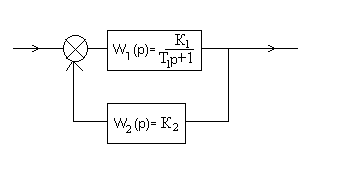
Решение:
Передаточная функция соединения:
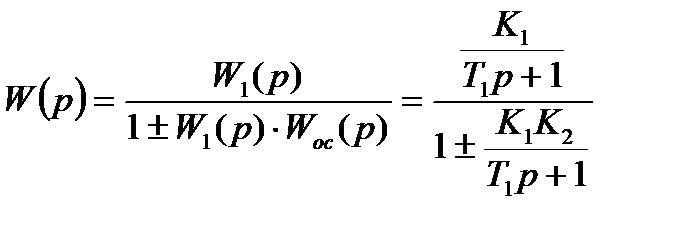
где К – коэффициент усиления
Т – постоянная времени
Приведем знаменатель дроби к общему знаменателю и сократим числитель и знаменатель на (Т1р+1), при этом получим:
W(р)=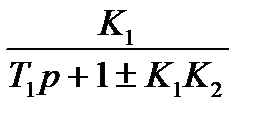 
Приведем полученное выражение к передаточной функции одного из типовых звеньев – апериодическому звену первого порядка W(р)=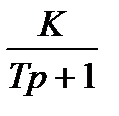 
, для этого поделим числитель и знаменатель на ( 
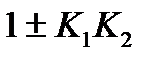). Получим W(р) = 
,
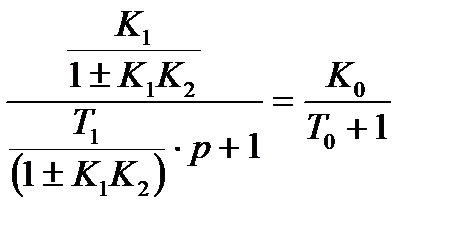где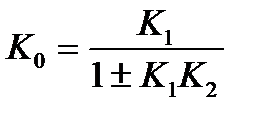 
, а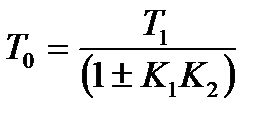 
,
т.е. звено остается апериодическим, но изменяется коэффициент передачи и постоянная времени. При введении ООС (знак «+») чувствительность падает,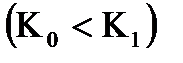 
а быстродействие 
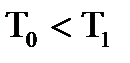растет. При введении ПОС - обратное явление.
2) Интегрирующее звено охвачено жесткой ОС.
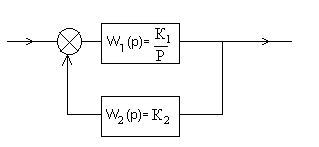
Решение:
Передаточная функция соединения:
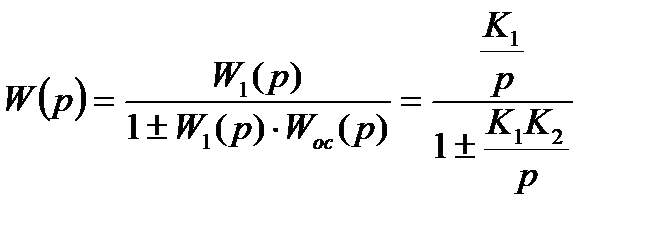
Приведем знаменатель дроби к общему знаменателю, числитель и знаменатель сократим на «р»; получим
W(р) =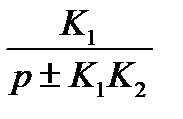 
Приведем полученное выражение к передаточной функции одного из типовых звеньев – апериодическому звену первого порядка W(р) 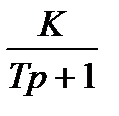, для этого поделим числитель и знаменатель на ( 
) , получим: W(р) =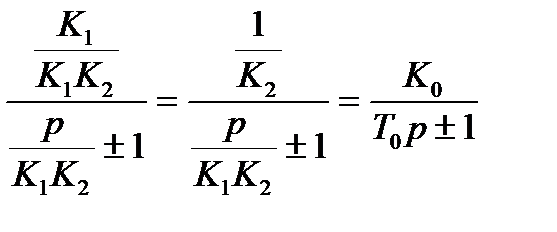 
,
где К0=1/К2, Т0=1/К1К2.
Т.е. при охвате интегрирующего звена жесткой ОС, оно становится
апериодическим звеном первого порядка, а значит из астатического звена превращается в статическое (происходит изменение структуры). При ООС оно устойчиво, при ПОС - неустойчиво.
3) Апериодическое звено 1-го порядка охвачено гибкой (дифференцирующей) обратной связью.
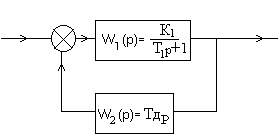
Решение:
Передаточная функция соединения:
Приведем знаменатель дроби к общему знаменателю и сократим числитель и знаменатель на (Т1р+1), при этом получим: W(р)=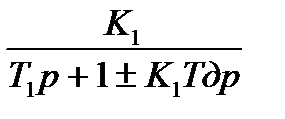 
,
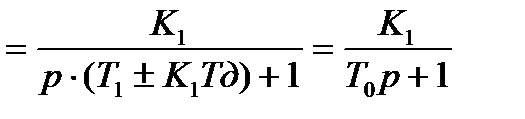где Т0=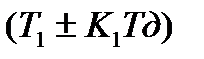 
.
Т.е. при охвате апериодического звена первого порядка гибкой ООС постоянная времени увеличивается, а - гибкой ПОС - уменьшается, коэффициент передачи и структура звена не изменяются.
Задание:
1. Определить как изменяются параметры и структура двух апериодических звеньев первого порядка при охвате их гибкой обратной связью. Произвести анализ полученной системы. Исходные данные для расчета взять из таблицы 1, согласно варианту.
Таблица 1
| Вариант № | К1, 1/сек | 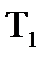, с
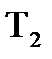| , с
|  , с
|
| 1 | 10 | 0,03 | 0,3 | 0,15 |
| 2 | 10 | 0,03 | 0,2 | 0,2 |
| 3 | 20 | 0,02 | 0,2 | 0,3 |
| 4 | 20 | 0,02 | 0,3 | 0,15 |
| 5 | 15 | 0,03 | 0,15 | 0,1 |
2. Произвести расчет:
W(p)=____________________________________________________________
_________________________________________________________________
K=_______________________________________________________________
T=_______________________________________________________________
3. Определить изменилась ли структура звена и его параметры
_________________________________________________________________
_________________________________________________________________
4. Составить программы определения величин K и Т на языке программирования высокого уровня
5. Вычислить на компьютере величины K и Т
Контрольные вопросы:
1. Для чего вводятся в САР корректирующие устройства?
2. Какие бывают корректирующие звенья
3. Изменится ли структура интегрирующего звена, если охватить его жесткой ОС?
4. Какие параметры изменяются в САР при охвате ее жесткой ОС?
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ КОЛЛЕДЖ РАДИОЭЛЕКТРОНИКИ,
ТЕЛЕКОММУНИКАЦИИ и БЕЗОПАСНОСТИ
РАБОЧАЯ ТЕТРАДЬ
ДИСЦИПЛИНА «ОСНОВЫ СИСТЕМ УПРАВЛЕНИЯ»
Вариант №
Выполнил студент___________________
Группы_________
Проверил преподаватель __________Фридман Г.М.
Оценка: ______________
Уфа 2015
Лабораторная работа № 1
«Решение задач операторным методом»
Цель работы: Исследовать возможности операторного метода при решении дифференциальных уравнений, описывающих работу системы.
Образовательные результаты, заявленные во ФГОС третьего поколения:
Студент должен
уметь:
- решать задачи операторным методом;
знать:
- типовые динамические звенья САУ, их соединения в системы, передаточные функции и амплитудо-фазо-частотные (АФЧХ) и логарифмические амплитудо-фазо-частотные характеристики (ЛАХ) и (ЛФХ) звеньев и систем;
-
Дата: 2018-11-18, просмотров: 238.
