При растяжении и сжатии
Литература: Степин П. А. § 10, Ицкович Г. М. § 2.6–2.8
При изучении этой темы необходимо уделить основное внимание вопросу испытания материалов, основным механическим характеристикам прочности материала: пределов пропорциональности, упругости, текучести и прочности (временное сопротивление), учесть, что числовые их значения условны, так как для их нахождения соответствующие силы делят на первоначальную площадь поперечного сечения испытываемого образца.
При опытном изучении деформации растяжения очень важной характеристикой является пластичность материала, которая характеризуется величиной относительного удлинения после разрыва образца
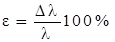
и относительного сужения площади поперечного сечения
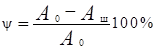, где
А0 – первоначальная площадь сечения образца,
Аш – площадь сечения шейки образца после разрыва.
Вопросы для самопроверки
1. Между какими величинами выражает зависимость диаграмма растяжения?
2. Как строится диаграмма растяжения?
3. Что называется пределом пропорциональности?
4. Что называется пределом упругости?
5. Что называется пределом текучести?
6. Что называется пределом прочности?
7. Каким механическим характеристикам материала соответствуют точки А, В, С, D на диаграмме растяжения (рис. 9)?
s
D
С Е
А В
e
Рис. 9
8. Какие материалы принято считать пластичными, хрупкими?
9. Какие механические характеристики, полученные при его испытании на растяжение, служат для оценки пластичности?
10. Какая деформация возникла в теле, если после снятия нагрузки размеры и формы тела полностью восстановились?
11. В чем заключается явление наклепа? Как получают наклеп в деталях и как от него избавляются?
12. На каком участке диаграммы растяжения пластичного материала выполняется закон Гука? Как графически определить модуль упругости?
13. Какой вид имеет диаграмма сжатия пластического материала?
14. Какой вид имеет диаграмма сжатия чугуна? Чем она отличается от диаграммы растяжения этого материала?
15. Можно ли определить предел прочности пластичного материала при испытании его на сжатие?
16. Предел прочности материала при растяжении sпч.р = 120 Н/мм2. Предел прочности этого же материала на сжатие sпч.с = 500 Н/мм2. Определите, какой это материал.
а) хрупкий,
б) пластичный.
ТЕМА 4
Срез и смятие
Литература: Степин П. А. § 23–26, Ицкович Г. М. § 4.1–4.2
|
Разрушения, возникающие при таком виде нагружения, когда внешние силы действуют перпендикулярно оси бруса, равны по абсолютному значению и противоположны по направлению, лежат в близко расположенных плоскостях, как, например, при резке листа металла, называют срезом (рис. 10).
На срез работают различные соединительные детали: шпонки, штифты, заклепки, болты.
При практических расчетах элементов конструкций на прочность при срезе следует иметь в виду, что эти расчеты носят условный характер и выводы сопротивления материалов могут быть применим лишь при введении некоторых допущений:
1. В поперечных сечениях элементов возникают только поперечные силы;
2. Касательные напряжения равномерно распределены по площади поперечного сечения;
3. Если элемент имеет несколько сечений среза, то возникающие в них поперечные силы одинаковы;
4. Внешние силы, сдвигающие соединительные элементы, равномерно распределены между соединительными элементами.
С учетом двух последних допущений поперечная сила в сечении соединительного элемента:
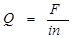, где F – внешняя сила, приложенная к соединительным элементам,
i – число плоскостей среза одного элемента,
n – число элементов.
Условие прочности при срезе имеет вид:
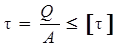, где [τ] – допускаемое касательное напряжение.
При выборе допускаемых напряжений на срез пользуются следующими соотношениями:
для хрупких материалов [τ] = (0,8…1,0) [σр] и
для пластичных материалов [τ] = (0,5…0,6) [σр].
Условие прочности при срезе позволяет выполнять проектный (определение общей площади среза) и проверочный расчеты, а также определять значения допускаемой нагрузки.
Деформация материала часто сопровождается смятием материала в местах соприкосновения отдельных элементов конструкции: так, смятию подвергается поверхность детали, по которой происходит ее касание с шайбой или гайкой затянутого болтового соединения, боковая поверхность заклепки и поверхность скрепляемых предметов в месте соприкосновения с заклепкой.
Считают, что напряжения смятия распределяются по поверхности контакта равномерно. Условно для упрощения расчета допускают, что напряжения смятия распределяются равномерно по площади проекции поверхности контакта на диаметральную плоскость.
Проверка на смятие производится: в случае разнородных материалов, для более мягкого материала, например при соединении двух деревянных брусков болтом проверяется на смятие древесина.
Расчетное уравнение на смятие имеет вид:
,
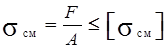где σсм – фактическое напряжение на смятие,
F – нагрузка,
А – площадь смятия,
[σсм] – допускаемое напряжение на смятие.
Допускаемое напряжение на смятие принимают [σсм] = (1,7…2,0) [σ], где
[σ] – допускаемое напряжение на сжатие.
Вопросы для самопроверки
1. Что называется деформацией сдвига?
2. Что называется абсолютным и относительным сдвигом?
3. Напишите формулы для определения абсолютного сдвига и касательных напряжений при сдвиге.
4. Как определяется величина действительных напряжений в поперечном сечении бруса при чистом сдвиге (срезе)?
5. Сформулируйте условие прочности при расчете на срез.
6. Какую механическую характеристику прочности материала нужно знать, чтобы определить силу давления пробойника на лист для вырубки в нем отверстия?
7. Определить толщину листа t, в котором пробили квадратное отверстие со стороной а = 18 мм, если предел прочности при срезе 
tпч = 400 Н/мм2, а величина силы F необходимой для пробивания отверстия равна 320 кН (рис. 11).
Рис. 11
8. Что такое смятие? На каких допущениях основаны расчеты на смятие?
9. Как определяется площадь смятия, если поверхность смятия плоская и если поверхность смятия цилиндрическая?
10. По какой формуле ведется расчет на смятие?
11. Шпилька Æ 20 мм прикрепляет к стене стальной лист сечением 100´8 мм (рис. 12). Чему равны напряжения среза и смятия шпильки и напряжение растяжения в листе, если F = 40 кН.
Рис. 12
12. Сформулируйте закон Гука при сдвиге. Каков физический смысл модуля сдвига?
13. Какая существует зависимость между модулем упругости первого и второго рода?
14. Как рассчитываются заклепочные соединения на срез и смятие?
15. По какому сечению в заклепочном соединении проводится проверка листов на разрыв?
ТЕМА 5
Кручение, геометрия сечений
Литература: Степин П. А. § 27–31, § 35–39, Ицкович Г. М. § 6.1–6.6, § 5.1–5.3
В теории изгиба и кручения важную роль играют моменты инерции сечения. Необходимо вспомнить и повторить из теоретической механики правила нахождения центра тяжести сечения и статических моментов плоских фигур.
Необходимо уяснить вычисление моментов инерции для простейших плоских фигур (прямоугольника, треугольника, круга).
Рассматривая теорему о моменте инерции сечения относительно оси, параллельной центральной (Iy1 = Iy + a2A), необходимо понять, что теорема справедлива только в том случае, если ось у проходит через центр тяжести фигуры.
Важно уяснить, что сумма моментов инерции относительно двух взаимно перпендикулярных осей равна полярному моменту инерции относительно точки пересечения этих осей.
Приступая к изучению раздела «Кручение», следует отметить, что данную деформацию испытывают такие детали машин, как валы, пружины, иногда болты при затяжке гайки ключом и др. Деформация кручения появляется при нагружении бруса парами сил, плоскости действия которых перпендикулярны к его оси. Моменты этих пар называют вращающими моментами.
При вычислении вращающих моментов пользуются формулой:
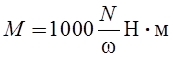, где М – вращающий момент в Н×м,
N – мощность в кВт,
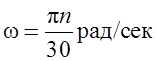угловая скорость,
n – число оборотов в минуту.
Необходимо уяснить те допущения, на которых основана элементарная теория кручения стержней круглого сечения: крайние сечения остаются плоскими, расстояния между поперечными сечениями не изменяются, радиусы, проведенные на торцевых сечениях, остаются прямолинейными и поворачиваются вместе с сечениями на некоторый угол.
Следует разобраться в построении эпюры крутящих моментов. Эпюра показывает изменение величины крутящего момента по длине вала. Необходимо уметь самостоятельно выполнять вывод формулы для напряжений при кручении стержня круглого сечения.
При кручении напряжение распределяется по поперечному сечению неравномерно (в линейной зависимости от расстояния точки до полюса сечения)
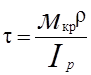, где τ – касательное напряжение в точке, находящейся на расстоянии ρ от оси бруса.
Мкр – крутящий момент в поперечном сечении,
ρ – расстояние до точки сечения,
Ip – полярный момент инерции площади сечения,
Опасными считаются все точки контура сечения, геометрическими характеристиками прочности и жесткости сечения являются соответственно полярный момент сопротивления и полярный момент инерции, значения которых зависят не только от площади, но и от формы сечения. Рациональным (т. е. дающим экономию материала) является кольцевое сечение, имеющее по сравнению с круглым сплошным меньшую площадь при равном моменте сопротивления (моменте инерции).
Необходимо уметь рассчитывать диаметр вала из условия прочности:
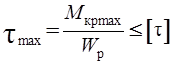и условия жесткости:
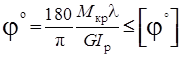, где
Wp – полярный момент сопротивления площади сечения,
l – длина вала,
G – модуль упругости при сдвиге,
Ір – полярный момент инерции площади сечения.
Для бруса из пластичного материала принимают [τ] = (0,55…0,6) [σр], для валов из конструкционных сталей обычно принимают [τ] = 20…50 МПа.
Допускаемый угол закругления в машиностроении принимают:
[φ°] = 0,25…1,00 град/м.
Вопросы для самопроверки
1. Как нужно нагрузить прямой брус, чтобы он испытывал только кручение?
2. Как определить вращающий момент, передаваемый шкивом (зубчатым колесом и т. д.), если известна передаваемая мощность и угловая скорость?
3. Чему должна быть равна алгебраическая сумма вращающихся моментов для равномерно вращающегося вала?
4. Что называется крутящим моментом в поперечном сечении бруса?
5. Какая разница между крутящим и скручивающим или вращающим моментом?
6. Что такое эпюра крутящих моментов? Как производится ее построение? Сформулируйте правило знаков при определении величины крутящего момента.
7. Выберите из приведенных на рис. 13 эпюр крутящих моментов ту, которая соответствует схеме нагружения вала, приведите схемы напряжения, которые будут соответствовать остальным эпюрам крутящих моментов.
а) 4 кНм 3 кНм 12 кНм 5 кНм
б) 5 кНм 8 кНм
4
7 кНм
в)
5 кНм
4 кНм
3 кНм
г)
4 кНм 7 кНм
5 кНм
д)
2 кНм 5 кНм
4 кНм
Рис. 13
8. Какие напряжения возникают в поперечном сечении круглого стержня при кручении? Как находится их величина в произвольной точке поперечного сечения?
9. Что называется полярным моментом инерции сечения? Какова размерность этой величины? По каким формулам вычисляется полярный момент инерции круга и кругового кольца?
10. По какому закону распределяются напряжения в поперечном сечении круглого бруса при кручении?
11. Какая геометрическая характеристика сечения характеризует при кручении:
а) его прочность;
б) его жесткость?
12. Зависит ли напряжение, возникающее при кручении:
а) от материала бруса;
б) от формы поперечного сечения (круг или кольцо)?
13. Какие точки поперечного сечения являются опасными при кручении бруса? Для каких точек сечения напряжение вычисляется по формуле t = Мкр / Wp?
А
D В
о
С
Рис. 12
14. Как записывается условие прочности при кручении? Что такое полярный момент сопротивления? По каким формулам вычисляются его значения для круга и для кругового кольца?
15. Какой величиной характеризуется величина деформации при кручении?
16. По какой формуле определяется угол поворота какого–либо поперечного сечения бруса, имеющего ступенчато–переменное поперечное сечение и нагруженного несколькими скручивающими (вращающими) моментами?
17. Зависит ли угол закручивания сечения: а) от материала бруса; б) от формы поперечного сечения?
18. Во сколько раз изменится угол закручивания бруса, если при прочих равных условиях: а) увеличить длину бруса в два раза; б) увеличить диаметр бруса в два раза? Как отразятся подобные изменения на прочности бруса?
19. Определить диаметр вала, показанного на рис. 13,а, считая его по всей длине постоянным, если [t] = 40 МПа.
20. Напишите математическое выражение условия жесткости при кручении. Сколько различных видов расчета можно производить из этого условия?
ТЕМА 6
Поперечный изгиб
Литература: Степин П. А. § 45–54, § 58–60, Ицкович Г. М. § 7.1–7.9, § 7.13
Приступая к изучению этой темы необходимо уяснить, что теория изгиба построена при следующих допущениях и предположениях (рис. 15):
1. Геометрическая ось бруса, т. е. ось, проходящая через центры тяжести сечений, есть прямая линия;
2. Внешние силы рис.15 (нагрузки), изгибающие брус, лежат в одной плоскости, проходящей через геометрическую ось бруса, и все нагрузки перпендикулярны к геометрической оси бруса;
3. Плоскость действия нагрузок является плоскостью симметрии бруса;
4. Поперечные сечения бруса, плоские до деформации изгиба, остаются плоскими и после деформации;
5. Деформации бруса незначительны.
Изгибом называют такой вид деформации бруса, при котором в его поперечных сечениях возникают два силовых фактора – поперечная сила Q и изгибающий момент М, для определения численных значений которых используется метод сечений. Необходимо помнить, что поперечная сила в данном сечении равна алгебраической сумме внешних сил, расположенных только по одну сторону (справа или слева) от рассматриваемого сечения, а изгибающий момент в данном сечении равен алгебраической сумме моментов внешних сил (расположенных слева или справа от сечения), взятых относительно центра тяжести сечения. При этом надо строго придерживаться правила знаков для поперечной силы и изгибающего момента. Поперечная сила считается положительной, если внешние силы стремятся сдвинуть левую часть балки относительно правой вверх или правую часть балки относительно левой – вниз. Правило для поперечной силы показано на рис. 16.
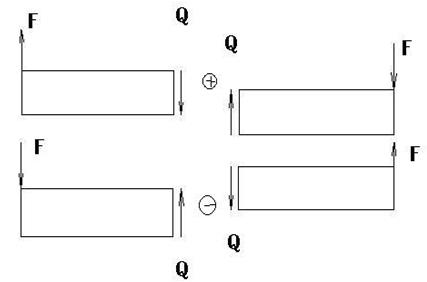
Рис. 16
Правило знаков для изгибающих моментов: внешним моментам, изгибающим мысленно закрепленную в рассматриваемом сечении отсеченную часть балки выпуклостью вниз, приписывается знак плюс, а моментам, изгибающим отсеченную часть балки выпуклостью вверх, – знак минус (рис. 17).
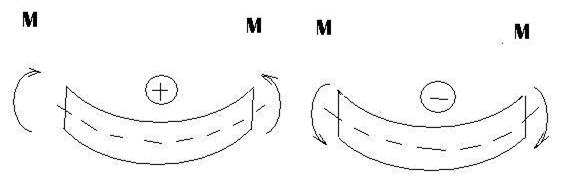
Рис. 17
Следует научиться свободно строить эпюры поперечных сил и изгибающих моментов. Для проверки правильности построения эпюр целесообразно пользоваться теоремой Журавского, устанавливающей зависимость между изгибающим моментом и поперечной силой:
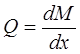, т. е. поперечная сила равна производной от изгибающего момента по абсциссе сечения х.
Интенсивность распределения нагрузки:
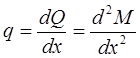, т. е. вторая производная от изгибающего момента по абсциссе сечения х равна интенсивности распределенной нагрузки.
Необходимо уметь выводить формулу для определения нормальных напряжений в производной точке сечения балки:
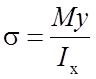, где
М – изгибающий момент в данном сечении балки,
у – расстояние точки сечения от нейтральной оси,
Ix – осевой момент инерции сечения балки.
Из формулы для определения нормальных напряжений в производной точке можно получить расчетное уравнение на изгиб. Обозначив допускаемое напряжение на изгиб [σ], получим расчетное уравнение:
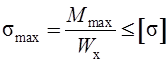, где
Мmax – наибольший изгибающий момент в сечении балки,
Wx – осевой момент сопротивления сечения.
Условие прочности позволяет выполнять три вида расчетов: проверочный расчет балки на прочность, определение допускаемых размеров сечения и расчет допускаемых действующих на балку нагрузок.
Рис. 18
После этого следует перейти к изучению вопроса об определении углов поворота поперечных сечений и прогибов балок. Для их определения целесообразно использовать универсальные уравнения.
Линейное перемещение у центра тяжести сечения называется прогибом. Наибольший прогиб обозначают f. Сечение балки поворачивается вокруг нейтральной линии сечения на некоторый угол φ, который называется углом поворота сечения. Условие жесткости при изгибе записывают в виде:
f ≤ [f]; φmax ≤ [φ].
Допускаемый прогиб назначают в долях пролета балки l.
Для валов принимают [f] = (0,0002...0,0010)l.
Допускаемые углы поворота сечений вала в местах, где расположены подшипники, принимают в пределах 0,001...0,005 рад.
Вопросы для самопроверки
1. Как нужно нагрузить прямой брус, чтобы он испытывал только прямой изгиб?
2. Что называется поперечной силой и изгибающим моментом в данном сечении балки?
3. Как находится поперечная сила в каком–либо сечении балки? Сформулируйте правило знаков для определения поперечной силы.
4. Как находится изгибающий момент в каком–либо сечении балки? В каком случае изгибающий момент считается положительным?
5. Определите поперечную силу и изгибающий момент в каждом поперечном сечении балки на рис. 19.
F = 12 кН q = 8 кН/м
М = 2 кН×м 1 2 3
0,2 м 0,5 м 0,5 м 1,4 м 0,4 м 1,2 м
1 2 3
Рис. 19
6. Выберите из приведенных на рис. 20 эпюр изгибающих моментов ту, которая соответствует схеме нагружения балки. Приведите схемы нагружения балки, которые соответствуют остальным эпюрам изгибающих моментов.
а)
q = 8 кН/м F = 5 кН
3 м 2 м
б)
25 кН×м
8 кН×м
М
в)
М
51 кН×м
10 кН×м
г)
5 кН×м
41 кН×м М
Рис. 20
7. Напишите формулу для определения нормального напряжения в произвольной точке поперечного сечения бруса, работающего на изгиб. Какая геометрическая характеристика сечения характеризует его прочность при изгибе?
8. Как распределяются нормальные напряжения по поперечному сечению при изгибе?
9. Зависит ли возникающее при изгибе нормальное напряжение: а) от материала балки; б) от формы поперечного сечения?
10. Какие точки поперечного сечения балки являются опасными? Для кааких точек сечения нормальные напряжения вычисляют по формуле s = Ми/Wх.
11. Как записывается условие прочности при изгибе?
12. Что называется осевым моментом сопротивления площади сечения?
13. Напишите формулы для определения осевых моментов сопротивления круга, кольца, прямоугольника.
14. Какие формулы поперечных сечений рациональны для балок из пластичных материалов?
15. Какие формулы поперечных сечений следует применять для чугунных балок?
16. Во сколько раз изменится прочность балки, если при прочих равных условиях: а) увеличить диаметр балки в два раза; б) увеличить в два раза длину консольной балки, нагруженной силой на конце консоли (консольной называется балка с опорой в виде заделки)?
17. Для балки, показанной на рис. 20, подберите ее диаметр, приняв [s] = 160 МПа.
18. В каких плоскостях возникают касательные напряжения при изгибе? Как находится их величина?
19. Как записываются дифференциальные уравнения изогнутой оси балки?
20. Напишите универсальные уравнения для определения перемещений при изгибе.
21. В чем состоит сущность расчета на жесткость при изгибе?
ТЕМА 7
Сложное сопротивление
Литература: Степин П. А. § 68–72, § 75–81, Ицкович Г. М. § 8.1–8.3, § 9.1–9.4
На практике часто встречаются случаи, когда в результате действия нагрузки в поперечных сечениях бруса одновременно появляется несколько компонентов внутренних сил. Тогда говорят, что брус находится в условиях сложного сопротивления. Таковы, например, случаи одновременного изгиба в двух плоскостях (косой изгиб) (рис. 21), одновременного растяжения или сжатия с изгибом (рис. 22) и, в частности, внецентренного растяжения (сжатия) одновременного кручения и изгиба (рис. 23).
Рис. 22
Рис. 21 Рис. 23
Задачи на сложное сопротивление решаются исходя из принципа независимости действия сил. Этот принцип позволяет получить окончательный результат решения задачи при совместном действии различных силовых факторов путем наложения (суммирования) результатов, вызванных каждым внешним силовым фактором в отдельности.
Наиболее часто на практике в поперечных сечениях бруса возникают следующие комбинации внутренних силовых факторов: два изгибающих момента, действующие во взаимно перпендикулярных плоскостях; продольная сила и изгибающие моменты; изгибающие и крутящий моменты; продольная сила и крутящий момент. Следует иметь в виду, что напряжение s надо рассматривать как алгебраическую сумму нормальных напряжений, вызванных растягивающими и изгибающими внешними силовыми воздействиями, а касательное напряжение τ – как алгебраическую сумму касательных напряжений в данной точке, вызванных кручением и изгибом.
Необходимо более детально рассмотреть задачу об определении напряжений и деформаций для трех случаев сложного сопротивления: косого изгиба, внецентренного растяжения (сжатия), совместного действия изгиба и кручения.
Вопросы для самопроверки
1. Что называется напряженным состоянием в данной точке деформируемого тела?
2. Какие имеются виды напряженного состояния материала?
3. Как определить напряжение на наклонной площадке растянутого стержня?
4. Как называются площадки, по которым действуют наибольшие и наименьшие нормальные напряжения?
5. Какие напряжения называются главными?
6. Чему равно наибольшее касательное напряжение в случае плоского и объемного напряженного состояния?
7. Напишите формулу обобщенного закона Гука.
8. Зачем применяются гипотезы прочности?
9. Как формируются гипотезы прочности наибольших касательных напряжений и удельной потенциальной энергии формоизменения?
10. Какие формулы служат для определения величин эквивалентных напряжений по гипотезам прочности наибольших касательных напряжений и удельной потенциальной энергии формоизменения?
11. Какой вид деформации бруса называется косым изгибом?
12. По какой формуле определяется нормальное напряжение при косом изгибе?
13. В каких точках поперечного сечения возникают наибольшие напряжения при косом изгибе?
14. Может ли балка круглого поперечного сечения испытывать косой изгиб?
15. Как находят напряжения в произвольной точке поперечного сечения при внецентренном растяжении или сжатии?
16. Какие напряжения возникают в поперечном сечении стержня при изгибе с кручением?
17. Какие точки поперечного сечения вала, испытывающего кручение и изгиб, являются опасными? Для каких точек сечения эквивалентные напряжения вычисляют по формуле sэ = Мэ / Wx?
18. Как пишутся условия прочности вала на совместное действие изгиба и кручения по третьей и четвертой теории прочности?
19. Как находится величина расчетного момента при изгибе с кручением вала по третьей и четвертой теориям прочности?
20. Вычислите эквивалентный момент по третьей теории прочности, приняв для опасного сечения вала Ми = 380 Н×м и Мк = 320 Н×м. Определите диаметр вала, приняв [s] = 80 МПа.
ТЕМА 8
Продольный изгиб
Литература: Степин П. А. § 83–89, Ицкович Г. М. § 12.1–12.4
При изучении явления продольного изгиба необходимо обратить внимание на то, что при сжатии длинных стержней бывают случаи, когда при постепенном увеличении нагрузки резко меняется форма равновесия и напряженное состояние, в результате чего может быть внезапное разрушение.
Если сжимающие силы будут больше предельной величины, то ось стержня изогнется и стержень будет подвергаться, кроме сжимающей силы, изгибающему моменту (рис. 24 а, б).
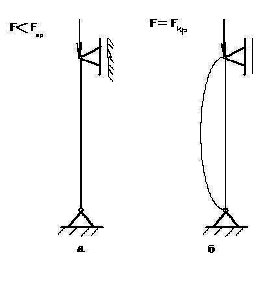
Рис. 24
F – действующая на стержень сжимающая сила,
Fкр – критическая сила, т. е. сжимающая центрально приложенная сила, при которой стержень еще устойчиво сохраняет прямолинейную форму равновесия
Величина критической силы определяется по формуле Эйлера:
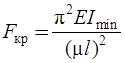, где
Е – модуль упругости 1-го рода материала стержня,
μ – коэффициент приведения длины стержня,
Imin – наименьший осевой момент инерции сечения,
l – длина стержня,
Fкр – величина критической силы.
Зная величину критической силы Fкр и площадь сечения стержня А, можно определить величину критического напряжения:
,
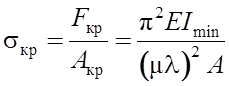так как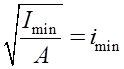 
представляет собой радиус инерции сечения и
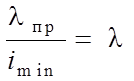есть гибкость стержня, то величина критического напряжения выражается формулой:
.
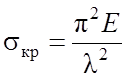Нужно обратить особое внимание на предел применимости формулы Эйлера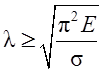 
. При гибкости меньше предельной формула Эйлера неприменима, расчет стержня на устойчивость выполняют по эмпирической формуле Ясинского sкр=а – bl, где a и b – коэффициенты, зависящие от материала. Следует также четко представлять себе, что при расчетах на устойчивость в отличие от расчетов на прочность предельное напряжение (здесь – критическое напряжение σкр) зависит не только от материала бруса, но и его геометрических размеров, формы сечения, а также от способа закрепления концов.
В обоих случаях λ £ λпред расчет стержня на продольный изгиб можно вести при помощи коэффициента понижения допускаемого напряжения на простое сжатие. Расчетная формула имеет вид:
Fдоп = j[s]сж×A, коэффициент φ зависит от гибкости и материала стержня.
Вопросы для самопроверки
1. В чем заключается явление потери устойчивости сжатого стержня?
2. Какую форму обретает центрально–сжатый стержень, если сжимающая его сила больше критической?
3. Какая сила называется критической?
4. По какой формуле находится величина критической силы?
5. Что называется гибкостью стержня?
6. Как учитывается влияние способов закрепления концов стержня?
7. Перечислите основные способы закрепления концов стержня и назовите коэффициенты приведения длины, учитывающие их влияние на величину критической силы.
8. Какой из показанных на рис. 24 стержней, выполненных из одинакового материала, одинаковой длины и поперечного сечения, потеряет устойчивость при меньшем значении сжимающей силы?
а) F б) F в) F г) F
|
9. При какой гибкости стержня применима формула Эйлера для подсчета критической силы?
10. Во сколько раз изменится значение критической силы для стержня большой гибкости, если: а) длину стержня увеличить в два раза; б) диаметр стержня уменьшить в два раза?
11. На рисунке 26 показаны поперечные сечения трех сжатых стержней. Какое сечение (круг или кольцо) при равной площади сечения и прочих равных условиях потеряет устойчивость при большем значении критической силы? Какое сечение (круг, кольцо или прямоугольник) менее рационально с точки зрения устойчивости стержня?
Y Y Y
X X X
 | |  |
a) б) в)
Рис. 26
12. Какой момент инерции подставляется в формулу Эйлера?
13. Определите критическую силу для стержня (рис. 25, в) длиной 1,5 м, квадратного сечения 20´20 мм и выполненного из ст. 3. Модуль продольной упругости материала Е = 200 ГПа.
14. Как производится проверка стержней на устойчивость при помощи коэффициента j?
15. Как подбирается сечение стержня при расчете на устойчивость?
тесты для проверки знаний по всему курсу
| № вопр. |
Вопрос
варианты ответа
Установите соответствие:
Дата: 2019-12-22, просмотров: 408.
