Литература: Степин П. А. § 7–9, § 11–20, Ицкович Г. М. § 2.1–2.5, § 2.9–2.11
Изучение темы необходимо начинать с выяснения вопроса о внутренних силовых факторах, действующих в сечении бруса. Применение метода сечений позволяет найти величину и направление равнодействующей внутренней (продольной) силы упругости в рассматриваемом сечении. Принято считать, что внутренняя растягивающая сила положительна, а сжимающая – отрицательна. Поэтому неизвестную продольную силу N всегда направляют от сечения (рис. 3), предполагая, что в рассматриваемом сечении возникает растяжение. Величина продольной силы N определяется из условия равновесия отсеченной части, а именно: сумма сил, действующих по оси х, равна нулю при условии равновесия бруса.
 SFix = F – N = 0, и следовательно N = F.
SFix = F – N = 0, и следовательно N = F.
Если при расчете продольная сила получается положительной, это значит, что она действительно направлена от сечения и является растягивающей. Если N получается отрицательной, то она является сжимающей.
|
При изучении растяжения и сжатия прямого бруса следует обратить особое внимание на гипотезу плоских сечений, которая справедлива и при других видах нагружения бруса. Сущность ее заключается в том, что плоские сечения, нормальные к оси бруса до деформации, остаются и после деформации плоскими и нормальными к его оси, а отсюда следует, что продольные элементы бруса растягиваются одинаково, силы упругости будут распределяться по сечению бруса равномерно, а поэтому напряжение во всех точках сечения определяется по формуле σ = N / A, где N – внутренняя сила, А – площадь поперечного сечения, которая является геометрической характеристикой прочности и жесткости, форма сечения значения не имеет, все точки сечения равноопасны.
Мерой деформации растяжения является относительное удлинение

ε = Δ l / l, где l – первоначальная длина бруса, Δl = l1 – l – абсолютное удлинение. Величина ε не имеет размерности и часто выражается в процентах.
|
|
σ = Εε, где σ – напряжение,
Ε – модуль продольной упругости (модуль упругости первого рода или модуль Юнга),
ε – относительное удлинение (или осевое укорочение).
Модуль продольной упругости имеет размерность напряжения МПа или Па (1 МПа = 106 Па) и характеризует жесткость материала, его способность сопротивляться упругому деформированию.
Для участка бруса длиной l, на котором постоянны продольная сила и площадь поперечного сечения, закон Гука можно записать в виде:
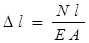 .
.
Это вторая форма закона Гука. Произведение ЕА называют жесткостью сечения. При расчетах на растяжение и сжатие используют основной принцип прочности детали: действующие или расчетные напряжения ни в одной точке детали не должны превышать допускаемые напряжения.
Так как при растяжении (сжатии) во всех точках сечения напряжения одинаковы, то при расчете бруса на прочность определяют положение наиболее напряженного (опасного) поперечного сечения. Если брус имеет постоянное по его длине поперечное сечение, то опасным является сечение, в котором возникает наибольшая продольная сила N. Если значение продольной силы во всех сечениях одинаково, то опасным является сечение с наименьшей площадью. Для определения опасного сечения бруса при изменяющихся по его длине площади поперечного сечения и продольной силе необходимо строить эпюру нормальных напряжений.
Условие прочности бруса при растяжении (сжатии), составленное для опасного сечения, имеет вид:
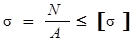 .
.
Условие прочности в словесной форме можно записать следующим образом:
| Действующее (расчетное) напряжение = | Внутреннее усилие | ≤ Допускаемое напряжение |
| Характеристика поперечного сечения |
Форма сечения бруса не влияет на его прочность при растяжении (сжатии). Форму сечения бруса необходимо знать только для определения размеров сечения при известном сечении площади.
С помощью условия прочности выполняют три вида расчетов: проверочный расчет, проектный расчет и определение допускаемой нагрузки.
Надо знать, что в ряде случаев необходимые для расчета бруса усилия невозможно найти только из уравнений равновесия. Такие задачи называют статически неопределимыми. При решении таких задач уравнения, которых не хватает для определения усилий, составляют из условия деформации бруса или системы.
Вопросы для самопроверки
1. Как нужно нагрузить прямой брус, чтобы он испытывал только растяжение (сжатие)?
2. Чем отличаются внутренние силовые факторы, возникающие при растяжении и сжатии?
3. Что называется продольной силой в сечении бруса? Как ее определить?
4. Что называется эпюрами продольных сил и нормальных напряжений? Как они строятся?
5. Определите продольную силу в каждом из поперечных сечений бруса (рис. 5) и постройте эпюры продольных сил.
3 2 1

50 кН 20 кН
3 2 1
Рис. 5
6. Выберите из приведенных на рис. 6 эпюр продольных сил ту, которая соответствует схеме нагружения бруса. Приведите схемы нагружения бруса, которые будут соответствовать остальным эпюрам продольных сил.
 20 кН 12 кН 8 кН
20 кН 12 кН 8 кН
а)

20 кН 8 кН
б)
6кН
 в)
в)
16 кН 8 кН
4 кН
 г)
г)
20 кН 4 кН
8 кН
д)

8 кН 6 кН
4 кН
Рис. 6
7. Что такое продольная и поперечная деформация бруса при растяжении (сжатии)? Напишите формулы для определения величин абсолютного и относительного удлинения или укорочения.
8. Что такое коэффициент Пуассона? Отчего зависит его величина?
9. По какой формуле определяется величина напряжения в поперечном сечении стержня?
10. Как распределяются напряжения по поперечному сечению бруса при растяжении (сжатии)?
11. Какая геометрическая характеристика сечения характеризует его прочность и жесткость при растяжении (сжатии)?
12. Зависит ли возникающее при растяжении (сжатии) напряжение:
– от материала бруса;
– от формы поперечного сечения?
13. Сформулируйте закон Гука и приведите формулу, выражающую этот закон.
14. Как определяется удлинение (укорочение) участка бруса с постоянным поперечным сечением и постоянной силой по всей его длине?
15. Какая величина в формуле закона Гука характеризует жесткость материала?
16. Во сколько раз изменится удлинение бруса, если при прочих равных условиях:
а) увеличить длину бруса в два раза;
б) увеличить диаметр бруса в два раза?
Как отразятся подобные изменения на прочности бруса?
17. Стальной стержень квадратного сечения, у которого модуль продольной упругости Е = 2 · 105 МПа, длина L = 0,6 м, закреплен одним концом и нагружен на другом конце растягивающей силой F = 40 кН. Определите:
а) нормальное напряжение в поперечном сечении;
б) изменение длины стержня.
18. Что называется допустимым напряжением материала? Почему оно должно быть ниже предела пропорциональности данного материала?
19. До какого предельного напряжения, являющегося механической характеристикой пластичного материала, можно нагружать брус, не опасаясь появления пластической деформации?
20. Для какого материала допустимое напряжение определяют по пределу текучести sт, а для какого по пределу прочности sв?
21. Что называется коэффициентом запаса прочности и каковы его численные значения, исходя из свойств материала?
22. Сформулируйте условия прочности и запишите в математической форме это условие при расчете на растяжение и сжатие.
23. Сколько различных видов расчета можно произвести с помощью условия прочности?
24. Напишите формулы, по которым:
а) проверяется действительное напряжение в сечении бруса;
б) подбирается площадь поперечного сечения и определяется величина допустимой нагрузки при заданном значении бруса.
25. При проверке прочности различных элементов конструкции, для материала которых допускаемое напряжение принято 160 МПа, фактические расчетные напряжения оказались равными 110, 155, 160, 167 и 180 МПа. Какие из перечисленных случаев соответствуют:
а) недостаточной прочности;
б) недостаточной жесткости;
в) достаточной прочности и экономичности?
26. Для бруса, показанного на рис. 7, определить диаметр, считая его по всей длине постоянным. Допускаемое напряжение для материала (Ст 3) принять равным 160 МПа.

12 кН 5 кН
Рис. 7
27. Определить допустимое значение нагрузки F по условию прочности стержня СВ, выполненного из стальной полосы 3´8 мм.
Принять [s] = 160 МПа, А D = 0,5м, D В = 0,7м.

Рис. 8
28. Какие системы (конструкции) называются статически определимыми и какие – статически неопределимыми?
29. Каков порядок решения статически неопределимых задач?
30. Что называется напряженным состоянием в точке тела? По каким формулам определяются нормальные и касательные напряжения, возникающие в наклонных площадях в случае плоского напряженного состояния?
ТЕМА 3
Дата: 2019-12-22, просмотров: 950.