Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Сложное

Сопротивление

–

в поперечных сечениях стержня действуют несколько силовых факторов (внутренних усилий), одновременно учитываемых при расчете на прочность.

 

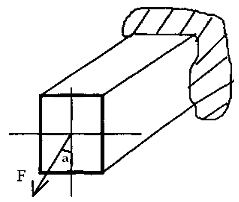
Косой изгиб

–

возникает в том случае, когда внешние силы, перпендикулярные оси стержня, не лежат в одной плоскости, проходящей через главную ось его поперечного сечения.

 

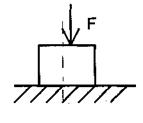
Внецентренное сжатие

–

продольная нагрузка не в центре тяжести поперечного сечения, а с некоторым смещением (эксцентриситетом) относительно главных осей сечения.

 

Эквивалентный момент

–

момент, который входит в расчетную формулу аналогично расчету на изгиб вместо изгибающего момента, который зависит от изгибающих и крутящих моментов, а также от принятой гипотезы прочности,

,

.

 

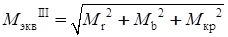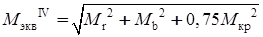Тема 10. Продольный изгиб

Продольный

Изгиб

–

изгиб стержня, связанный с потерей устойчивости прямолинейной формы его равновесия.

 

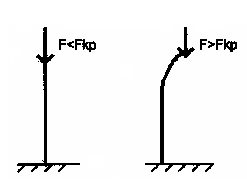
Критическая

Сила

–

наименьшее значение сжимающей силы, при которой сжатый стержень теряет способность сохранять прямолинейную форму равновесия .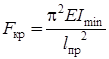

 

Плоскость

Наименьшей

Жесткости

–

плоскость, в которой лежит одна из главных осей, относительно которой момент инерции минимален – I_min.

 

Гибкость

Стержня

–

безразмерная геометрическая характеристика сжатого стержня, показывающая его сопротивляемость потере устойчивости, она одновременно отражает и длину стержня и жесткость его поперечного сечения .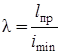

 

Приведенная длина стержня

–

равна фактической длине стержня, умноженной на некоторый коэффициент μ, зависящий от способов закрепления концов стержня .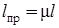

 

Коэффициент приведения

Длины стержня

–

коэффициент μ, характеризующий способ закрепления концов сжатого стержня.

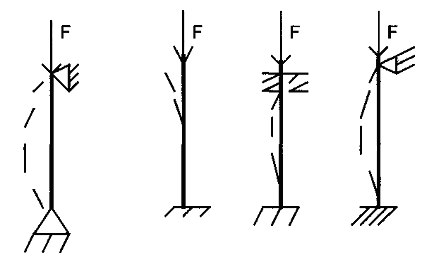
μ = 1                            μ = 2,0           μ = 0,5               μ = 0,7

 

Радиус инерции сечения

–

геометрическая характеристика 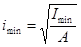 формы и размеров поперечного сечения сжатого стержня.

 

Критическое

Напряжение

–

нормальное напряжение в поперечном сечении сжатого стержня, соответствующее критическому значению сжимающей силы .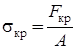

 

Коэффициент

Запаса

Устойчивости

–

число [n_y], показывающее, во сколько раз фактически действующая или допускаемая нагрузка меньше критической. Коэффициент запаса устойчивости принимают несколько большим коэффициента запаса прочности.

 

Коэффициент продольного

Изгиба

–

коэффициент уменьшения основного допускаемого напряжения на сжатие или коэффициент продольного изгиба. .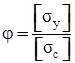

Зависит от материала стержня и его гибкости. Расчет на устойчивость по коэффициентам φ имеет вид: .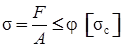

 

                                   

 

Общие методические указания

По изучению курса

 

Изучение курса «Сопротивление материалов» (науки о прочности, жесткости и устойчивости деформируемых под нагрузкой элементов машин и конструкций) следует начать с повторения раздела «Статика» (связи и реакции связей, равновесие тел, уравнения равновесия, геометрические характеристики сечений).

Освоение каждой темы должно обязательно сопровождаться составлением конспекта, ответами на вопросы для самопроверки, ознакомлением с методикой решения задач, решением рекомендуемых задач, ответами на тесты. Если при решении задач возникнут затруднения, следует воспользоваться имеющимися в пособии методическими указаниями к решению задач, а также словарем понятий и терминов. Совершенно необходимо научиться решать задачи самостоятельно и соблюдать правила вычислений, используя калькулятор.

При выводе формул необходимо обращать особое внимание на физическую сущность явления и на те допущения и ограничения, которые делаются в процессе выводов. Необходимо хорошо разбираться в тех чертежах и рисунках, которыми сопровождаются выводы формул.

В процессе выполнения лабораторных работ студент знакомится с инструкциями по их выполнению, с испытательными машинами, измерительным инструментом, методами и видами экспериментального исследования конструкционных материалов, составляет отчет о проделанной работе, отвечает на вопросы, прилагаемые к инструкции лабораторной работы, и проходит компьютеризированный опрос по тестам.

Непременными условиями успешного овладения учебным материалом являются:

а) четкое понимание физического смысла рассматриваемых понятий;

б) свободное владение методом сечений;

в) осознанное применение геометрических характеристик прочности и жесткости поперечных сечений;

г) самостоятельное решение достаточно большого числа задач.