Пусть задача нелинейного программирования ставится в следующем общем виде: найти такие значения переменных х1, х2,…, хn, которые отвечают условиям:

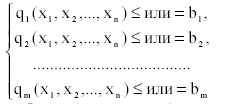
и приносят требуемый экстремум (максимум или минимум) целевой функции

f = f(х1, х2,…, хn), (13.2)

где f(х1, …, хn) и qi(х1, …, хn) ( m , 1 i = ) - действительные нелинейные,

регулярные функции n действительных переменных.

По своим общим свойствам задачи нелинейного программирования могут

существенно отличаться от линейных. Например, область допустимых решений может уже быть невыпуклой, а экстремум целевой функции может наблюдаться в любой точке допустимой области. Существенно отличаются и методы решения нелинейных задач. Рассмотрим лишь некоторые подходы к решению этих задач.

Прежде всего также справедлив графический подход при решении простейших задач нелинейного программирования. Так, если аргументами задачи являются переменные х1 и х2, то сначала на плоскости этих переменных строится область допустимых решений, а затем с помощью уровней целевой функции f(х1,х2) определяется оптимальная точка в области.

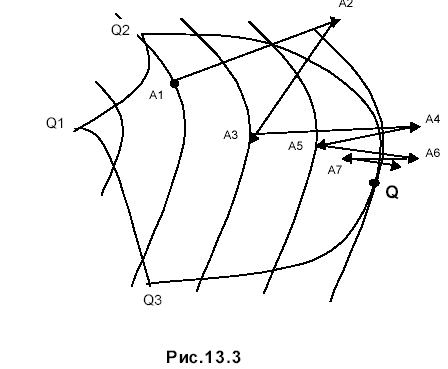
В нелинейном программировании для решения многих задач используется градиентный подход. Имеется целый ряд градиентных методов, сущность которых состоит в поиске оптимального результата с помощью градиента целевой функции - вектора, указывающего направление максимального возрастания цели для рассматриваемой точки. В общем случае процедура поиска совершается в итеративном режиме от первоначально выбранной точки к точкам с лучшим показателем. Пусть, например, . - о6ласть допустимых решений

рассматриваемой задачи, а итеративный процесс расчетов начинается с точки

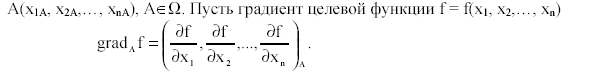
    Далее, сначала делается переход по градиенту целевой функции, а затем возврат в область . по градиенту к нарушенной границе О2 О3 области .. На рис. 13.3 показано так, что Ai с нечетными индексами принадлежат области ., а точки Аi с четными индексами не принадлежат .. По мере приближения к оптимальной точке Q направления рабочих градиентов сближаются. Поэтому идеальным критерием остановки процесса будет коллинеарность градиента цели и градиента нарушенной границы.

67. Понятие о параметрическом и целочисленном программировании.

Постановка и математич модель ЗЦЛП.

В задачах с неделимыми объектами на переменные накладываются условия целочисленности. Иногда эти условия распространяются на все переменные, иногда—на часть переменных.Рассматривают полностью целочисленную задачу

f=(n,j=1)∑CjXi max

(n,j=1)∑AijXj=bi, i=1,m

xj≥0, j=1,n

xi-целое,j=1,n

Теперь в отличие от общей задачи линейного программирования, оптимальный план не обязательно будет в вершине многогранника планов.Существуют следующие методы решения целочисленных задач:

1.Методы отсечения

2.Комбинаторные

3.Приближенные методы..

Параметрическое программирование – раздел математического программирования, посвящённый исследованию задач оптимизации, в которых условия допустимости и целевая функция зависят от некоторых детерминированных параметров.