Модели задач ЛП могут быть записаны в различных видах.
1. Развернутый вид записи модели
Z = c1 X1 + c2 X2 + … + cn Xn → min
a11 X1 + a12 X2 + … + a1n Xn = a1,
a21 X1 + a22 X2 + … + a2n Xn = a2,
……………………………………………
a m1 X1 + am2 X2 + … + amn Xn = am,
Xj ≥ 0, j = 1, n.
2. Свернутый вид:
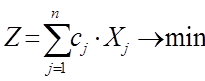
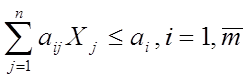 ,
,
Xj ≥ 0, j = 1, n.
3. Модель задачи ЛП в матричном виде:
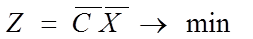
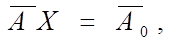 X ≥ 0
X ≥ 0


 Где
Где 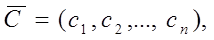
а11 а12 … а1n X1 a1
A= a21 a22 … a2n , X= X2 , A0 = a2
… … … … … …
am1 am2 … amn X3 am
4. Модель задачи ЛП в векторном виде:
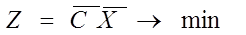
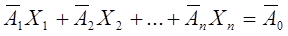
X ≥ 0




 Где
Где 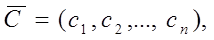
Х1 a11 a12 a1n a1
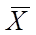 Х2 ,
Х2 , 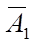 a21 ,
a21 , 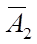 a22 ,
a22 , 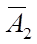 a2n ,
a2n , 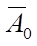 a2
a2
… … … … …
Хn am1 am2 am2 am
15. Переход от стандартной и общей формы задач ЛП к канонической. Теорема связи
Для перехода от общей или стандартной формы к канонической используют следующие приёмы.
1. Преобразование переменных. Если какая-то переменная Xk неположительна (Xk ≤ 0), то вводят новую переменную Xk ', так что Xk ' = –Xk . Очевидно, что Xk ' ≥ 0. После этого в каждом ограничении и целевой функции переменную Xk заменяют на [ – Xk '].
Если какая-то переменная Хt может принимать любые значения, то её заменяют разностью двух неотрицательных переменных Хt’ и Хt’’, т. е. полагают, что хt = Хt’ – Хt’’, где Хt’ 0 ≥ и Хt’’ ≥ 0.
2. Преобразование ограничений. Если какое–либо из ограничений в модели имеет вид неравенства, то оно преобразуется в равенство прибавлением (если неравенство имеет тип ≤) или вычитанием (если неравенство имеет тип ≥) из его левой части. Эти переменные называют балансовыми. Балансовые переменные входят в целевую функцию с коэффициентами нуль. Балансовая переменная принимает значение индекса последовательно после уже имеющихся. Если, например, система ограничений имеет 5 переменных, то первая балансовая переменная будет Х6, а вторая – Х7 и т.д.
Переход от канонической формы модели ЗЛП к стандартной
Для перехода от канонической формы к стандартной можно каждое из
уравнений заменить системой неравенств:
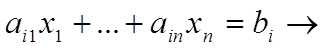
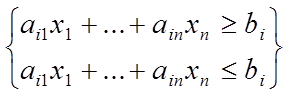
Другой способ состоит в приведении системы уравнений к специальному виду и дальнейшему исключению некоторых переменных.
С помощью метода Жордана-Гаусса выделяем в каждом уравнении базисную переменную. Такое выделение осуществляется с помощью эквивалентных (элементарных) гаусовских преобразований. К ним относятся:
а) умножение любого уравнения на константу отличную от нуля;
б) прибавление к любому уравнению любого другого уравнения, умноженного на любую константу.
Исходную систему линейных уравнений перед преобразованием удобно записывать в виде матрицы или таблицы:
Далее находим х1, х2 … хn . Далее подставляем в целевую функцию z выражениех1 и х2 … хn.
Записываем задачу в стандартной форме.
Понятие гиперплоскости полуплоскости, опорная гиперплоскость.

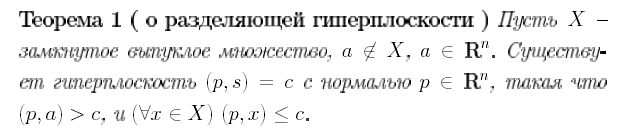

Геометрич. интерпретация системы ограничений и целевой функции в задачи ЛП


Дата: 2019-12-22, просмотров: 410.