Первая теорема двойственности.

Теорема: если одна из двойственных задач имеет оптимальный план, то и другая решима, т.е. имеет опт.план. При этом экстремальные значен.целевых функций совпадают (j=от 1 до n) Σcjxj*= (i=от 1 до m)Σbiyi* если в исходн. задаче целевая функция неограниченна на множестве планов, то в двойственной задаче система ограничений несовместна.

Вторая теорема двойственности и ее эконом.интерпритация.

Для того, чтобы допустимые решения пары двойственных задач были оптимальными, необходимо и достаточно выполнение условия: xj*(∑aij yi*-cj)=0, j от 1 до n, yi*(∑aij xj*-bi)=0, I от 1 до m. Это условия дополняющей нежесткости. Из них следует: если какое-либо ограничение двойств.задачи обращ-ся оптималь.планом в строгое равенство, то соответствующая компонента опт. плана двойственной задачи должно равняться нулю.Если же какая-то компонента опт. плана равна нулю, то соответствующее ограничение двойств.задачи обращается опт.планом в строгое равенство хj*>0 следовательно (i= от 1 до m)Σaij yi*=cj (затраты на пр-во продукции=цене) – Если продукция вошла в опт.план, то если затраты>цены, объем пр-ва=0 Σaij yi* >cj следовательно xj*=0 

yi*>0 следовательно (j=от 1 до n) Σaij xj*=bi (рас-ды рес-ов =запас рес-ов).

(j=от 1 до n) Σaij xj* <bi следовательно yi*=0

Смысл теоремы сводится к следующему:

-если стоимост.оценка рес-ов расход-х на пр-во ед.прод-ии=цене, то этот вид прод-ии входит в оптим.план ;

-если затраты превышают цену, то прод-ию производить не следует;

- еслирасход рес-ов=запасу, то стоимост.оценка этого рес-са положительна. Такой рес-с наз-ся дефицитным. Наибелее дефицит.рес-с обладает наибольшей оценкой;

-если рес-с израсходован неполностью, то его стоимост.оценка = 0.

61. Построение оптимального опорного плана двойственной задачи по симплексной таблице исходной задачи

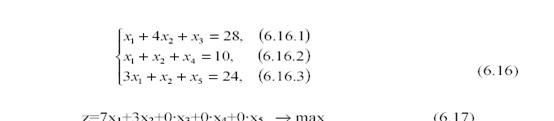
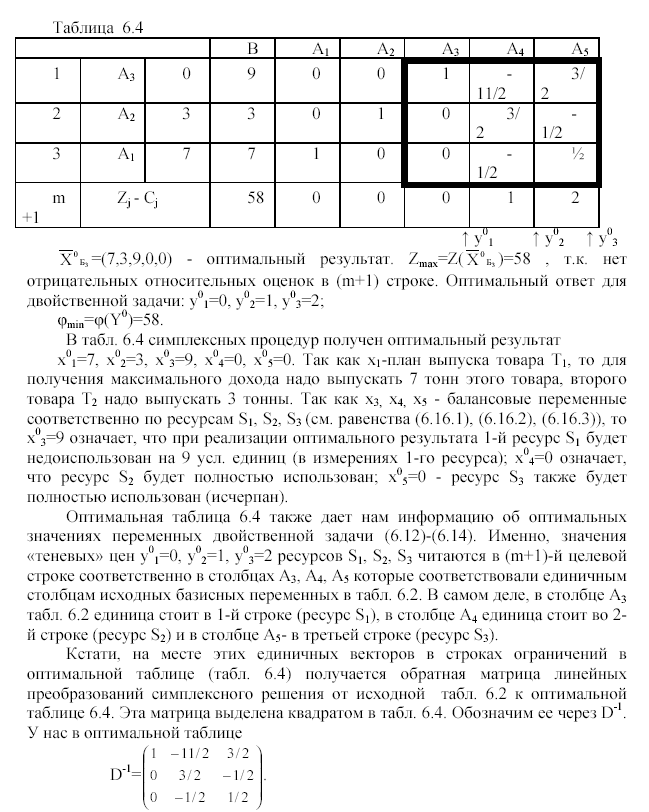
Информация из столбцов обратной матрицы линейных преобразований, приведших к оптимальному результату. Из столбцов матрицы D-1 можно почерпнуть весьма полезную информацию.

Столбец A3: «теневая» цена ресурса S2 равна y01=0, столбец остался

единичным и по первой строке можно прочесть, что x3=9, т.е. при реализации найденного оптимального плана 1-й ресурс окажется в избытке, причем этот избыток (недоиспользование) как раз составит 9 условных единиц.

Столбец A4: «теневая» цена ресурса S2 равна y02=1, ресурс будет полностью использован и его возможное увеличение будет вести к увеличению целевой функции (т.е. дохода). И т.к. y02=1, то увеличение ресурса S2 на 1 у.е. будет давать добавку по доходу на .Z = y02· .в2 = = 1.1 = 1 (тыс. грн.) (здесь .в2 -приращение ресурса S2 и .Z - соответствующее приращение дохода ). При таком приращении ресурса S2 максимальный доход уже составит Zmax=58 тыс. грн. + 1 тыс. грн = 59 тыс. грн. На рис. 6.2 проиллюстрирована эта ситуация, комментарий по отношению к которой будет приведен ниже. Из столбца A4 еще следует, что при увеличении ресурса S2 на 1 у.е. для новой оптимальной точки выпуск товара T1 сократится на ½ тонны (на пересечении строки базисной переменной x1 и столбца A4 стоит «-1/2»), а выпуск товара T2 увеличится на 3/2 тонны (т.к. в строке с базисной переменной x2 в столбце A4 имеем «3/2»).Сказанное по столбцу A4 будет ниже прокомментировано с помощьюграфических построений (рис. 6.2).Столбец A5: «теневая» цена ресурса S3 равна y03=2. Это означает, чтоувеличение ресурса S3 на 1 у.е. принесет добавку по Z на .Z = y03· .в3 = 2.1 =2(тыс. грн.) и составит Zmax=58 тыс. грн. + 2 тыс. грн = 60 тыс. грн. При этом, как следует из столбика A5 табл. 3, выпуск T1 увеличится на ½ тонны, а T2 уменьшится на ½ тонны. Запас по сырью S1 (см. 1-ю строку) увеличится на 3/2 у.е.