
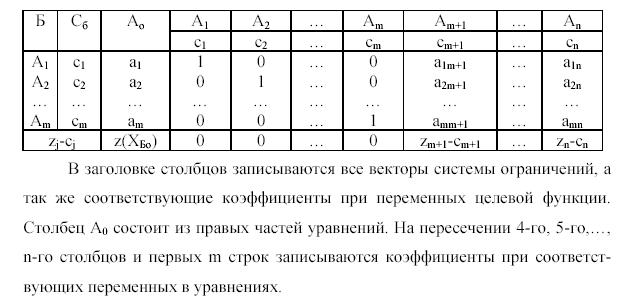


30. Теорема оптимальности плана задачи линейного программирования следствие из теоремы оценки оптимальности при решении задач симплекс методом.
Теорема 1: Если для некоторого вектора Āj в системе
Х1 + а1m+1Xm+1 + а1m+2Xm+2 + … + а1nXn = a1
Х2 + а2m+1Xm+1 + а2m+2Xm+2 + … + а2nXn = a2
…………………………………………………..
Xm + аmn+1Xm+1 + аmn+2Xm+2 + … + аmnXn = am
Выполняется соотношение Zj – cj > 0, то план ХБ0 не является оптимальным и можно перейти к плану ХБ1 такому, что Z (ХБ1) ≤ Z (ХБ0).
Здесь Zj = (С, Āj) – скалярное произведение векторов.
С – вектор, состоящий из коэффициентов при базисных переменных целевой функции Z
Āj – вектор, состоящий из коэффициентов разложения соответствующего вектора по векторам базиса.
cj – коэффициент целевой функции Z при переменной Хj
Следствие из теоремы: Если для всех векторов Ā1, Ā2, …, Ān некоторого опорного плана Х выполняется соотношение Zj – cj < 0, то опорный план Х является оптимальным. Величины (Zj – cj) – называются оценками оптимальности соответствующих векторов.
Таким образом теорема и следствие позволяют установить, является ли очередной опорный план оптимальным и, если не является, то необходимо перейти к другому опорному плану, при котором значение целевой функции будет меньше.
Замечание. В теореме и следствии предполагается, что задача находится в канонической форме с целевой функцией на минимум. Однако симплекс-методом моно решать и задачи с целевой функцией на максимум. В этом случае при анализе значений оценок используется их противоположный смысл, то есть план будет оптимальным, если все оценки оптимальности будут не отрицательными (положительным или отрицательным).
Выбор вектора, вводящегося в базис и выводящегося из базиса. Симплексное отношение.
Для перехода к новому опорному плану необходимо один из свободных векторов 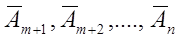 ввести в базис, а какой-то из базисных векторов вывести. Для введения в базис выберем вектор, имеющий хотя бы одну положительную координату. Пусть таким вектором будет вектор А m+1 .
ввести в базис, а какой-то из базисных векторов вывести. Для введения в базис выберем вектор, имеющий хотя бы одну положительную координату. Пусть таким вектором будет вектор А m+1 .
Разложению –
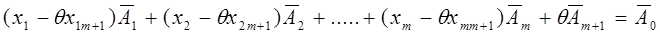 соотв. вектор, кот. будет являться опорным планом, если его координаты будут неотрицательными, а кол-во положительных координат будет равняться m.
соотв. вектор, кот. будет являться опорным планом, если его координаты будут неотрицательными, а кол-во положительных координат будет равняться m.
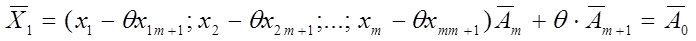
Координаты вектора Х1 должны быть неотрицательными, т.е. 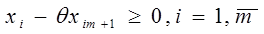 .
.
Если 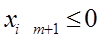 , то эта координата будет неотрицательной.
, то эта координата будет неотрицательной.

Пусть минимум в соотношении (5) был получен при i =1, тогда если взять
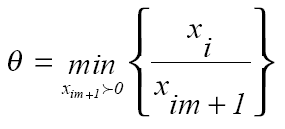
то первая координата вектора 1 х станет равной нулю.
Соотношение (6) называется симплексным отношением. Таким образом, мы перешли от исходного опорного плана 0 х (базисные векторы А1,А2,…Аm) к опорному плану 1 х (базисные векторы А2,А3,…,Аm,Am+1).
Разрешающий элемент таблицы, его выбор. Правило полных жордановых исключений для перерасчета симплекс таблицы.
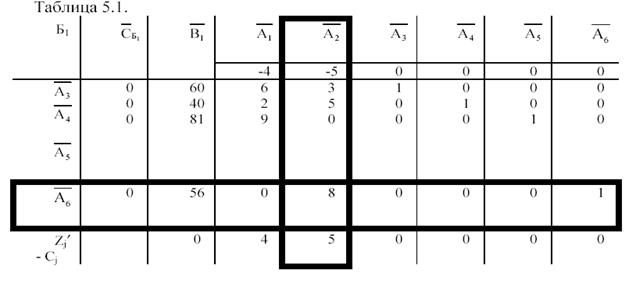



Дата: 2019-12-22, просмотров: 379.