Важный частный случай функциональных рядов представляют собой степенные ряды, т.е. ряды вида 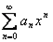 или, в более общем случае,
или, в более общем случае, 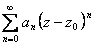 . Поскольку при замене
. Поскольку при замене 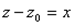 ряд
ряд 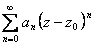 переходит в ряд
переходит в ряд 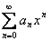 , достаточно рассмотреть эти последние ряды.
, достаточно рассмотреть эти последние ряды.
Теорема 1. Если степенной ряд 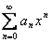 сходится в точке
сходится в точке 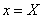 , то он сходится абсолютно для любого значения
, то он сходится абсолютно для любого значения 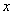 такого, что
такого, что 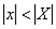 .
.
Доказательство. Поскольку  - сходится,
- сходится, 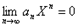 . Следовательно,
. Следовательно, 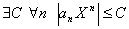 . (Действительно, взяв
. (Действительно, взяв 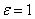 , получим, что при
, получим, что при 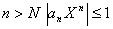 . Тогда в качестве
. Тогда в качестве 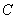 можно взять наибольшее из конечного набора чисел
можно взять наибольшее из конечного набора чисел 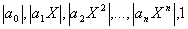 ). Тогда
). Тогда 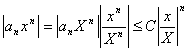 . Так как
. Так как 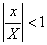 , прогрессия
, прогрессия 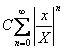 сходится. Значит, по первой теореме о сравнении, сходится ряд
сходится. Значит, по первой теореме о сравнении, сходится ряд 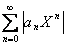 , т.е. исходный ряд абсолютно сходится.
, т.е. исходный ряд абсолютно сходится.
Эта теорема позволяет выяснить структуру множества, на котором сходится степенной ряд.
Во-первых, очевидно, что любой степенной ряд сходится в точке 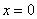 . Кроме того, есть ряды, которые сходятся только в этой точке, например, ряд
. Кроме того, есть ряды, которые сходятся только в этой точке, например, ряд 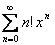 .
.
Если же ряд сходится в точках, отличных от 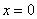 , то возможны два случая.
, то возможны два случая.
В первом из них множество чисел 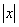 таких, что ряд сходится в точке
таких, что ряд сходится в точке 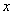 , неограничено сверху. Тогда ряд абсолютно сходится на всей числовой прямой, т.к.
, неограничено сверху. Тогда ряд абсолютно сходится на всей числовой прямой, т.к. 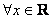 выберем
выберем 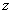 так, чтобы, во-первых,
так, чтобы, во-первых, 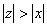 и, во-вторых, ряд
и, во-вторых, ряд 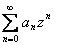 сходился. Тогда, по теореме 1, ряд
сходился. Тогда, по теореме 1, ряд 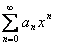 абсолютно сходится.
абсолютно сходится.
Во втором случае множество чисел 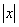 таких, что ряд
таких, что ряд 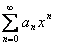 сходится, ограничено сверху. Обозначим через
сходится, ограничено сверху. Обозначим через 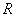 точную верхнюю грань этого множества. Число
точную верхнюю грань этого множества. Число 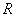 называется радиусом сходимости ряда. Из определения
называется радиусом сходимости ряда. Из определения 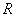 следует, что:
следует, что:
1. Если 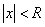 , то ряд
, то ряд 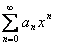 абсолютно сходится;
абсолютно сходится;
2. Если 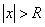 , то ряд
, то ряд 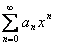 расходится.
расходится.
В случае, когда ряд сходится на всей числовой прямой 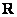 , полагают
, полагают 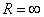 .
.
В точках 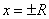 общего утверждения о сходимости сделать нельзя (т.е. бывают ряды, сходящиеся в обеих этих точках, бывают – сходящиеся лишь в одной из них, бывают – расходящиеся в обеих точках. Примеры будут приведены ниже).
общего утверждения о сходимости сделать нельзя (т.е. бывают ряды, сходящиеся в обеих этих точках, бывают – сходящиеся лишь в одной из них, бывают – расходящиеся в обеих точках. Примеры будут приведены ниже).
Найдем формулы, с помощью которых можно вычислить 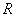 - радиус сходимости степенного ряда. Рассмотрим ряд
- радиус сходимости степенного ряда. Рассмотрим ряд 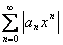 . Применим к его исследованию признак Даламбера.
. Применим к его исследованию признак Даламбера. 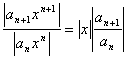 . Если существует
. Если существует 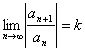 , и если
, и если 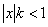 , то ряд сходится. Если же
, то ряд сходится. Если же 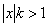 , то, начиная с некоторого места,
, то, начиная с некоторого места,  и общий член
и общий член 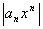 ряда
ряда 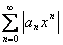 не стремится к 0, но тогда и общий член
не стремится к 0, но тогда и общий член 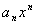 ряда
ряда 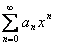 не стремится к 0 и ряд расходится.
не стремится к 0 и ряд расходится.
Иными словами, ряд сходится при 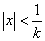 и расходится при
и расходится при 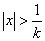 . Таким образом, число
. Таким образом, число  представляет собой радиус сходимости степенного ряда. (Если
представляет собой радиус сходимости степенного ряда. (Если 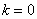 , то
, то 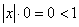 при всех
при всех 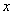 и ряд сходится на всей числовой прямой, что обозначается равенством
и ряд сходится на всей числовой прямой, что обозначается равенством 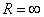 ).
).
Дадим другую формулу для радиуса сходимости. Применим к рассматриваемому ряду 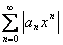 признак Коши.
признак Коши. 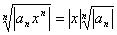 . Пусть существует
. Пусть существует 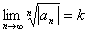 . Тогда, как и выше, при
. Тогда, как и выше, при 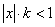 ряд сходится, а при
ряд сходится, а при 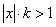 - расходится. Поэтому
- расходится. Поэтому 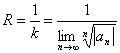 (при
(при 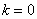 , разумеется,
, разумеется, 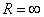 ).
).
Рассмотрим примеры.
Пример 1. 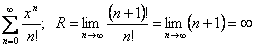 . Ряд абсолютно сходится на всей числовой прямой.
. Ряд абсолютно сходится на всей числовой прямой.
Пример 2. 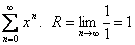 . В точках
. В точках 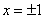 ряд, очевидно, расходится.
ряд, очевидно, расходится.
Пример 3. 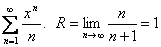 . В точке
. В точке 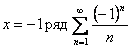 сходится по теореме Лейбница. В точке
сходится по теореме Лейбница. В точке 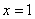 гармонический ряд
гармонический ряд 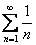 расходится.
расходится.
Пример 4. 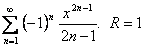 . В точках
. В точках 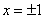 получается условно сходящийся ряд
получается условно сходящийся ряд 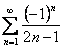 .
.
Пример 5. 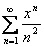 .
. 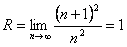 . В точках
. В точках 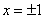 имеем ряд
имеем ряд 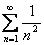 , который абсолютно сходится.
, который абсолютно сходится.
Теорема. Степенной ряд 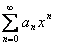 представляет собой функцию, непрерывную на
представляет собой функцию, непрерывную на 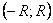 , где
, где 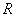 - радиус сходимости ряда.
- радиус сходимости ряда.
Доказательство.
Лемма. Пусть 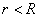 . Тогда
. Тогда 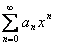 сходится на множестве
сходится на множестве 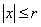 абсолютно и равномерно.
абсолютно и равномерно.
Доказательство. Так как 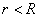 , ряд
, ряд 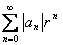 сходится. Так как
сходится. Так как 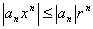 , можно применить теорему Вейерштрасса, из которой и следует утверждение леммы.
, можно применить теорему Вейерштрасса, из которой и следует утверждение леммы.
Замечание. Лемма отнюдь не утверждает равномерной сходимости степенного ряда на 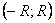 . Да это, вообще говоря, и неверно. Например, прогрессия
. Да это, вообще говоря, и неверно. Например, прогрессия 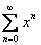 сходится на
сходится на 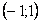 неравномерно. Однако этот ряд сходится равномерно на любом
неравномерно. Однако этот ряд сходится равномерно на любом 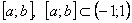 .
.
Пусть теперь 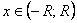 , т.е.
, т.е. 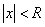 . Выберем
. Выберем 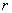 так, чтобы
так, чтобы 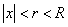 . Тогда, по доказанной лемме, ряд сходится на
. Тогда, по доказанной лемме, ряд сходится на 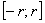 абсолютно и равномерно. Поскольку все функции
абсолютно и равномерно. Поскольку все функции 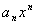 - непрерывные, сумма ряда есть непрерывная на
- непрерывные, сумма ряда есть непрерывная на 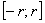 функция. Значит, эта функция непрерывна и в выбранной, произвольной точке
функция. Значит, эта функция непрерывна и в выбранной, произвольной точке 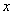 интервала
интервала 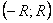 .
.
Следствие. (Единственность степенного ряда). Пусть 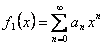 ,
, 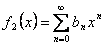 и в некоторой окрестности
и в некоторой окрестности 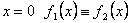 . Тогда
. Тогда 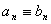 .
.
Доказательство. При 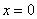 получаем:
получаем: 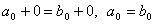 . Поэтому
. Поэтому 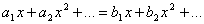 . При
. При 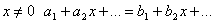 . В правой и левой частях стоят степенные ряды, а они, по-доказанному, есть непрерывные функции, поэтому равенство сохраняется при
. В правой и левой частях стоят степенные ряды, а они, по-доказанному, есть непрерывные функции, поэтому равенство сохраняется при 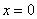 , откуда
, откуда 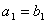 и т.д. (Отметим, что здесь существенно использована непрерывность ряда в точке
и т.д. (Отметим, что здесь существенно использована непрерывность ряда в точке 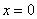 ).
).
Сформулируем без доказательства еще одну важную теорему.
Теорема. (Абель). Если ряд 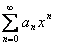 , имеющий сумму
, имеющий сумму 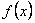 , сходится (хотя бы неабсолютно) при
, сходится (хотя бы неабсолютно) при 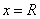 , то
, то 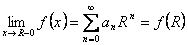 (т.е. сумма ряда непрерывна слева).
(т.е. сумма ряда непрерывна слева).
Теорема. Для любого 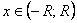
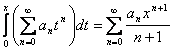 .
.
Доказательство. Пусть 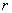 удовлетворяет неравенствам
удовлетворяет неравенствам 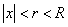 . Тогда степенной ряд сходится равномерно на
. Тогда степенной ряд сходится равномерно на 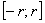 и его можно почленно проинтегрировать. Кроме того,
и его можно почленно проинтегрировать. Кроме того, 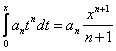 . Теорема доказана.
. Теорема доказана.
Теорема. Для любого 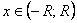
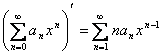 .
.
Доказательство. Выберем 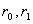 так, чтобы
так, чтобы 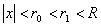 . По определению
. По определению 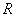 , ряд
, ряд 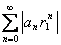 сходится. Поэтому
сходится. Поэтому 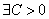 (см. доказательство теоремы 1):
(см. доказательство теоремы 1): 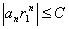 . Рассмотрим величину
. Рассмотрим величину 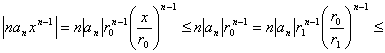
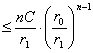 . По признаку Даламбера, ряд
. По признаку Даламбера, ряд 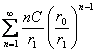 сходится, т.к.
сходится, т.к.  . Значит, мы оценили члены ряда
. Значит, мы оценили члены ряда 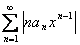 при
при 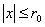 членами сходящегося ряда
членами сходящегося ряда 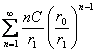 . Применяя теорему Вейерштрасса на
. Применяя теорему Вейерштрасса на 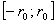 , получаем, что этот ряд равномерно сходится. Следовательно, почленное дифференцирование обосновано на отрезке
, получаем, что этот ряд равномерно сходится. Следовательно, почленное дифференцирование обосновано на отрезке 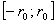 , а значит, и в точке
, а значит, и в точке 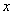 . Ввиду произвольности точки
. Ввиду произвольности точки 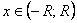 , теорема доказана.
, теорема доказана.
Важное замечание. Из доказанных теорем вытекает, что при интегрировании и дифференцировании радиус сходимости не уменьшается. Но увеличиться он также не может. Если бы, например, он увеличился и стал равен 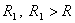 при интегрировании, мы продифференцировали бы этот полученный при интегрировании ряд и получили бы с одной стороны, ряд, совпадающий с исходным, а с другой стороны, имеющий радиус сходимости не меньший, чем
при интегрировании, мы продифференцировали бы этот полученный при интегрировании ряд и получили бы с одной стороны, ряд, совпадающий с исходным, а с другой стороны, имеющий радиус сходимости не меньший, чем 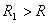 (по доказанному).
(по доказанному).
Итак, радиус сходимости степенного ряда не меняется при почленном интегрировании и дифференцировании.
Однако поведение в концевых точках 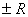 может меняться. Например, ряд
может меняться. Например, ряд 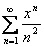 сходится на
сходится на 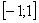 . При этом ряд
. При этом ряд 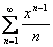 , получающийся из исходного дифференцированием, сходится только на
, получающийся из исходного дифференцированием, сходится только на 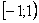 , а прогрессия
, а прогрессия 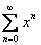 , получающаяся при дифференцировании ряда
, получающаяся при дифференцировании ряда 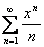 (сходящегося на
(сходящегося на 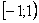 ), сходится на
), сходится на 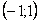 .
.
Рассмотрим теперь функцию 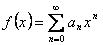 , представляемую степенным рядом в области его сходимости. Очевидно,
, представляемую степенным рядом в области его сходимости. Очевидно, 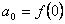 . Далее, последовательно применяем теорему о почленном дифференцировании ряда.
. Далее, последовательно применяем теорему о почленном дифференцировании ряда. 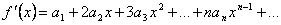 , откуда
, откуда 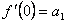 .
. 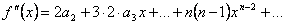 , откуда
, откуда 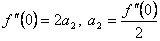 .
. 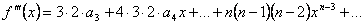 ,
, 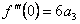 и т.д.
и т.д. 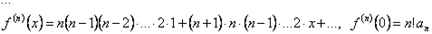 .
.
Следовательно, при всех 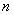
 . Таким образом,
. Таким образом, 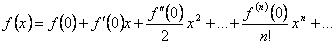 . Это можно сформулировать так: степенной ряд, сходящийся к
. Это можно сформулировать так: степенной ряд, сходящийся к 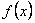 , представляет собой ряд Тейлора для своей суммы
, представляет собой ряд Тейлора для своей суммы 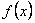 .
.
Если 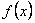 имеет производные произвольного порядка в точке
имеет производные произвольного порядка в точке 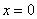 , то можно образовать соответствующий ей ряд Тейлора:
, то можно образовать соответствующий ей ряд Тейлора: 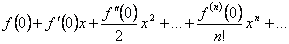 .
.
Важное замечание. Не всегда этот ряд сходится к самой функции 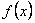 . Например, нетрудно доказать, что функция
. Например, нетрудно доказать, что функция 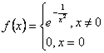 имеет производные произвольного порядка в точке
имеет производные произвольного порядка в точке 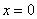 и все они равны 0, т.е.
и все они равны 0, т.е. 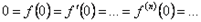 . Ряд Тейлора этой функции тождественно равен 0 и не совпадает с
. Ряд Тейлора этой функции тождественно равен 0 и не совпадает с 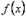 .
.
Необходимое и достаточное условие для того, чтобы ряд Тейлора функции 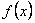 сходился к самой функции
сходился к самой функции 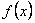 , можно сформулировать так: остаток
, можно сформулировать так: остаток 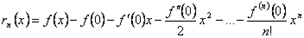 должен стремиться к 0 при
должен стремиться к 0 при 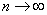 .
.
Дата: 2019-12-22, просмотров: 376.