Рассмотрим многочлен

,

он называется однородным степени n, если все его члены имеют один и тот же порядок n, то есть для каждого а_ij×хⁱ×у^j имеем i+j=n.

Определение 1. Функция Р(х,у) называется однородной степени n, если для любого k - числа - имеет место тождество

Р(k×х,k×у) = kⁿ×P(x,y).

Пусть дано уравнение

Р(х,у)dx+Q(x,y)dy=0. (1.8)

Если P(x,y),Q(x,y) - однородные функции одной и той же степени n, тогда (1.8) является однородным уравнением первого порядка.

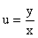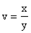Для решения таких уравнений пользуются подстановкой или , которая приводит к уравнению с разделяющимися переменными.

Пример.

х²+у²-2×х×у×у^/=0.

Предположим, что х×у ¹ 0. Тогда

.

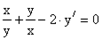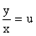следовательно, у = u×x , а отсюда dy = udx+xdu

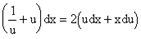
После приведения подобных и перегруппировки членов имеем

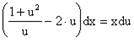
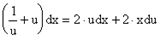
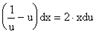
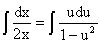Þ

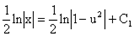
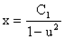следовательно, x²-y²=C₁×x - решение.

Сделаем проверку

1. Если х = 0 тогда C₀ = 0 и, следовательно x² = y² .

2. 1-u² = 0 .

Пусть теперь однородное дифференциальное уравнение имеет вид

у^/ = f(x,y) или .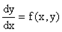

Тогда dy=f(x,y)dx, то есть при dy стоит коэффициент, равный единице, то есть имеем однородную функцию нулевой степени: следовательно, f(x,y) должна быть однородной функцией нулевой степени.

Линейные дифференциальные уравнения первого порядка.

Линейное уравнение имеет вид:

а(х)×у^/ + b(х)×y + c(x) = 0, (1.9)

где а(х), b(x), c(x) - заданные функции.

Если а(х) ¹ 0, то это уравнение можно записать в приведенном виде:

у^/ + Р(х)×у = f(x), (1.10)

где , ,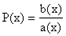

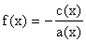тогда f(x) - свободный член.

Пусть Р(х) и f(x) в (1.10) непрерывны на (a,b).

Будем искать решение в виде y = u×v, где u - ненулевое решение соответствующего однородного уравнения

u^/ + P(x)×u = 0, (1.11)

a v - неизвестная функция. Тогда

y^/ = u^/×v + v^/×u. (1.12)

Подставим в (1.10) эти выражения. Получим

u^/×v + v^/×u + P(x)×u×v = f(x) (1.13)

v × (u^/+P(x)× u) + u×v^/ = f(x)

Учитывая, что имеет место (1.11), получим

u×v^/ = f(x). (1.14)

Следует u подобрать так, чтобы коэффициент при v был равен нулю.

Из (1.11) и (1.14) находим u и v, подставляем в y = u×v, причем u есть конкретное решение, отличное от нуля.

Пример. Необходимо найти частное решение

x×y^/-y = x².

Начальные условия:

.

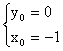Пусть у = 0 при х = -1.

Искомое решение запишем в виде y = u×v.

y^/ = u^/×v + v^/×u.

Подставим в уравнение, имеем

x×u^/×v + x×v^/×u - u×v = x².

После приведения подобных имеем

v×(x×u^/ - u) + x×u×v^/ = x².

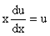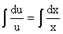Þ следовательно, lnu = lnx + lnC₀.

Если С₀ = 1 , значит, u = x.

Но тогда

x²×v^/ = x² и v = x + C₁.

y = x × ( x + C₁) = x² + C₁ × x - общее решение.

А если у₀ = 0 , то получим 1 + С₁×(-1) откуда С₁ = 1.

у = х² + х - частное решение.

Пример.

(х + у)×у^/ = 1.

, .

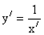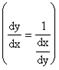Пусть

x = u×v, тогда 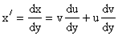и

v×u^/ + u×v^/ = x + y.

Учитывая, что х = u×v, имеем

v×(u^/-v) + u×v^/ = y

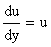следовательно, lnu = y, u = e^y,

Так как 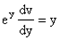, то имеем .

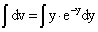Далее

v = -y×e^-y - e^-y + C.

x = u×v = -y-1 + C×e^y - общее решение.

y = -y-1 + C×e^y

начальные условия:

у₀ = 0, х₀ = 2.

2 = -1 + С Þ С = 1

х + у + 1 = е^у - частное решение.