Обыкновенным дифференциальным уравнением называется уравнение, связывающее между собой значения независимой переменной x, неизвестной функции y = f(x) и её производных (или дифференциалов):
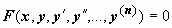 ; (1)
; (1)
(все три переменные x, y, F - действительны).
Опр. Порядком уравнения называется максимальный порядок n входящей в него производной (или дифференциала).
Пример: y(4) – y + x = 0 - уравнение четвёртого порядка.
Уравнение вида F(x, y, y/) = 0 называется уравнением первого порядка.
В простейших случаях оно может быть разрешено относительно у/ = f(x,y).
Общее решение имеет вид у = j(х,С), где С - константа.
Геометрически общее решение представляет собой семейство интегральных кривых.
Интегральные кривые обладают тем свойством, что все касательные в точке М(х,у) имеют наклон tga = f ’(x,y).
Если задать точку М0(х0,у0), через которую должна проходить интегральная кривая, то это требование называется начальным условием y = у0, х = х0 и тогда
у0 = j(х0,С0).
Определяется С - константа; в результате получаем частное интегральное решение у = j(х,С0).
В этом состоит задача Коши.
Опр. Частным решением уравнения (1) на интервале (a, b) (конечном или бесконечном) называется любая n раз дифференцируемая функция 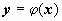 , удовлетворяющая этому уравнению, т.е. обращающая уравнение на этом интервале в тождество.
, удовлетворяющая этому уравнению, т.е. обращающая уравнение на этом интервале в тождество.
Так, функция y(x) = ex + x обращает уравнение : y(4) – y + x = 0 в тождество на всей числовой оси (y(4)(x) = ex; ex –(ex +x) + x = 0), т.е. является частным решением этого уравнения. Любое уравнение порядка 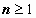 имеет множество частных решений (частным решением приведённого уравнения является и функция y(x) = sin(x) + x). Процедуру решения дифференциального уравнения часто называют интегрированием уравнения, при этом интегрировать приходится в общем случае ровно n раз, и при каждом интегрировании в решение входит очередная произвольная постоянная.
имеет множество частных решений (частным решением приведённого уравнения является и функция y(x) = sin(x) + x). Процедуру решения дифференциального уравнения часто называют интегрированием уравнения, при этом интегрировать приходится в общем случае ровно n раз, и при каждом интегрировании в решение входит очередная произвольная постоянная.
Опр. Общим решением (общим интегралом) уравнения (1) называется такое соотношение
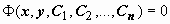 ; (2)
; (2)
что: 1. Любое решение (2) 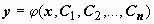 относительно y (для набора постоянных C1, C2, …, Cn из некоторой области n-мерного пространства) - частное решение уравнения (1);
относительно y (для набора постоянных C1, C2, …, Cn из некоторой области n-мерного пространства) - частное решение уравнения (1);
2. Любое частное решение уравнения (1) может быть получено из (2) при некотором наборе постоянных C1, C2, …, Cn.
Мы будем в основном рассматривать дифференциальные уравнения в форме, разрешённой относительно старшей производной:
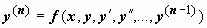 ;
;
и получать общее решение в форме
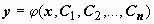 ;
;
решённой относительно неизвестной функции.
обыкновенным дифференциальным уравнением первого порядка называется уравнение
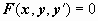 ;
;
где x - независимая переменная, y(x) - неизвестная функция. В форме, разрешённой относительно производной, уравнение первого порядка записывается так:
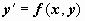 ;
;
Если пользоваться другим обозначением производной, то можно записать (6) как
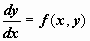 ;
;
Общее решение (общий интеграл) уравнения при n = 1 имеет вид 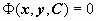 или
или 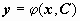 .
.
Дата: 2019-12-22, просмотров: 387.