Бесконечным числовым рядом называется выражение
u1+u2+...+un+... , (1) содержащее неограниченное число членов, где u1 , u2 , u3 , ... , un , ...
- бесконечная числовая последовательность; un называется общим членом ряда.
Для составления ряда нужно знать закон образования общего члена.
Например, если un = 2*n+1, то ряд имеет вид:
3, 5, 7, 9, ..., 501, 503, ..., n*2+1
Если un = (-1)n, то ряд имеет вид:
-1, +1, -1, +1, ..., -1, +1, ..., (-1)n
Сумма первых n членов ряда обозначается символом Sn и называется частичной суммой этого ряда. Таким образом,
Sn = u1 + u2 + ... + u n
или, короче,
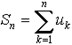
Определение: Ряд называется сходящимся, если сумма первых его n членов при n®¥ стремится к конечному пределу S, называемому суммой ряда.
Если ряд (1) сходится, т.е. имеет сумму S, то пишут
S = u1 + u2 + ... + u n + ...
Если же при n®¥ сумма Sn не имеет предела или
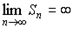
то ряд (1) называется расходящимся и не имеет суммы.
Типичным примером сходящегося ряда может служить ряд, полученный из бесконечно убывающей геометрической прогрессии
a + aq + aq 2 + aq 3 + ... + aq n-1 + ..., (2)
где -1 < q < 1
Действительно, для этого ряда
Sn = a + aq + aq 2 + aq 3 + ... + aq n-1 =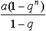 
При n®¥ qn®0 (так как | q |<1), поэтому
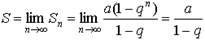
и ряд (2) будет сходящимся. Таким образом можно написать
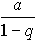= a + aq + aq 2 + aq 3 + ... + aq n-1 + ... .
Если q = 1, то ряд (2) имеет вид
a + a + a + a + ... + a + ... . (3)
Сумма Sn первых его n членов, равная na, по абсолютной величине неограниченно возрастает при неограниченном возрастании числа n. Таким образом, ряд (3) - расходящийся.
Если q = -1, то ряд (2) примет вид
a - a + a - a + a - a +... +(-1)n-1 a + ... . (4)
Ясно, что для этого ряда S2n=0 , S2n-1=a. т.е.сумма четного числа первых 2n членов ряда (4) стремится к нулю, а сумма нечетного числа первых 2n-1 его членов стремится к a.
Отсюда следует, что ряд (4) расходится, так как в сходящемся ряде как S2n так и S2n-1 стремятся к одному и тому же пределу S.
Ясно, что если | q |>1, то ряд (2) является также расходящимся.
Необходимый признак сходимости. Гармонический ряд.
Теорема: Пусть числовой ряд
u1+u2+...+un+... , (1)
сходится, а S - его сумма. Тогда при неограниченном возрастании числа n членов ряда его общий член un стремится к нулю
Доказательство. Из условия теоремы имеем
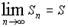
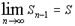
Так как
Sn - Sn-1 = un
то
Следует отметить, что этот признак является лишь необходимым, но не достаточным признаком сходимости ряда, так как можно указать ряд, для которого выполняется равенство
,
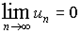а он, однако не является сходящимся.
Так гармонический ряд
,
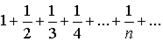для которого
,
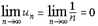расходится.
Но согласно доказанному необходимому признаку сходимости ряда, если
,
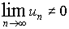то ряд (1) расходится.
В самом деле, если бы он сходился, то
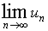
равнялся бы нулю.
Таким образом, доказанная нами теорема иногда позволяет, не вычисляя суммы Sn, сделать заключение о расходимости того или иного ряда. Например, ряд
,
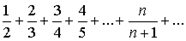расходится, так как
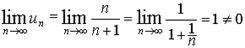
Достаточные признаки сходимости рядов с положительными членами.
Признаки сравнения
Если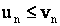 
, и ряд 
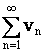сходится, то сходится и ряд 
.
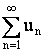Если 
, и ряд 
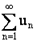расходится, то расходится и ряд 
.
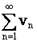Признаки сравнения можно сформулировать в такой форме:
Если заданы ряды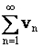 
, 
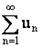и существует 
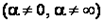, то ряды 
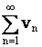и 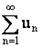сходятся либо расходятся одновременно.
Пример:
1. Исследуем сходимость ряда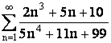 
. Очевидно, что 
.
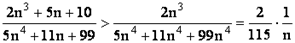Так как гармонический ряд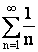 
расходится, то и ряд 
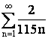также расходящийся, и, согласно признаку сравнения, данный ряд 
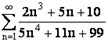расходится.
2. Исследовать сходимость ряда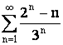 
. Имеем: 
.
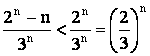Ряд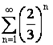 
сходится как сумма геометрической прогрессии со знаменателем 
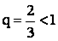. Следовательно, согласно признаку сравнения ряд 
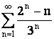сходится.
Признак Д’Аламбера
Если существует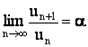 
то:
- при 
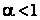ряд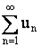 
сходится;
- при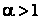 
ряд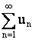 
расходится.
Радикальный признак Коши
Если существует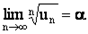 
то:
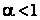- при ряд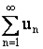 
сходится;
- при 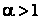ряд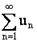 
расходится.
Интегральный признак Коши
Пусть задан ряд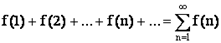 
, члены которого являются значениями непрерывной, положительной и монотонно убывающей функции 
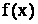на промежутке 
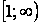. Тогда ряд 
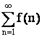сходится, если сходится несобственный интеграл 
.
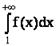Если же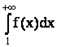 
расходится, то ряд 
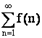также будет расходящимся.
Дата: 2019-12-22, просмотров: 232.
