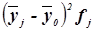Для расчета применяется формула средней арифметической простой:
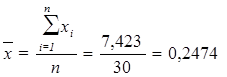 (8)
(8)
Причина расхождения средних величин, рассчитанных по формулам (8) и (5), заключается в том, что по формуле (8) средняя определяется по фактическим значениям исследуемого признака для всех 30-ти организаций, а по формуле (5) средняя вычисляется для интервального ряда, когда в качестве значений признака берутся середины интервалов 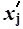 и, следовательно, значение средней будет менее точным (за исключением случая равномерного распределения значений признака внутри каждой группы).
и, следовательно, значение средней будет менее точным (за исключением случая равномерного распределения значений признака внутри каждой группы).
Задание 2
По исходным данным табл. 1 с использованием результатов выполнения Задания 1 необходимо выполнить следующее:
1. Установить наличие и характер корреляционной связи между признаками Среднесписочная численность работников и Выпуск продукции, образовав по каждому признаку пять групп с равными интервалами, используя методы:
а) аналитической группировки;
б) корреляционной таблицы.
2. Оценить тесноту корреляционной связи, используя коэффициент детерминации и эмпирическое корреляционное отношение.
Сделать выводы по результатам выполнения Задания 2.
Выполнение Задания 2
Целью выполнения данного Задания является выявление наличия корреляционной связи между факторным и результативным признаками, установление направления связи и оценка ее тесноты.
Факторный и результативный признаки либо задаются в условии задания, либо определяются путем проведения предварительного теоретического анализа. Лишь после того, как выяснена экономическая сущность явления и определены факторный и результативный признаки, приступают к проведению корреляционного анализа данных.
По условию Задания 2 факторным является признак Уровень производительности труда (X), результативным – признак Выпуск продукции (Y).
1. Установление наличия и характера связи между признаками Уровень производительности труда и Выпуск продукции методами аналитической группировки и корреляционной таблицы
1а. Применение метода аналитической группировки
При использовании метода аналитической группировки строится интервальный ряд распределения единиц совокупности по факторному признаку Х и для каждой j-ой группы ряда определяется среднегрупповое значение 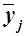 результативного признака Y. Если с ростом значений фактора Х от группы к группе средние значения
результативного признака Y. Если с ростом значений фактора Х от группы к группе средние значения 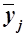 систематически возрастают (или убывают), между признаками X и Y имеет место корреляционная связь.
систематически возрастают (или убывают), между признаками X и Y имеет место корреляционная связь.
Используя разработочную таблицу 3, строим аналитическую группировку, характеризующую зависимость между факторным признаком Х – Уровень производительности труда и результативным признаком Y – Выпуск продукции. Макет аналитической таблицы имеет следующий вид (табл. 7):
Таблица 7
Зависимость суммы прибыли банков от объема кредитных вложений
| Номер группы | Группы организаций по уровню производительности труда, х | Число организаций, fj | Выпуск продукции, млн руб. | |
| всего | в среднем на одну организацию,
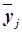
| |||
| 1 |
|
|
|
|
| 2 |
|
|
|
|
| 3 |
|
|
|
|
| 4 |
|
|
|
|
| Итого |
|
|
|
|
Групповые средние значения 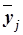 получаем из таблицы 3 (графа 4), основываясь на итоговых строках «Всего». Построенную аналитическую группировку представляет табл. 8.
получаем из таблицы 3 (графа 4), основываясь на итоговых строках «Всего». Построенную аналитическую группировку представляет табл. 8.
Таблица 8
Зависимость выпуска продукции организаций от выпуска продукции
| Номер группы | Группы организаций по уровню производительности труда, х | Число организаций, fj | Выпуск продукции, млн руб. | |
| всего | в среднем на одну организацию,
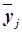
| |||
| 1 | 2 | 3 | 4 | 5=4:3 |
| 1 | 0,12 – 0,168 | 3 | 56 | 18,666 |
| 2 | 0,168 – 0,216 | 4 | 117,31 | 29,327 |
| 3 | 0,216 – 0,264 | 12 | 480,886 | 40,073 |
| 4 | 0,264 – 0,312 | 7 | 382,504 | 54,643 |
| 5 | 0,312 – 0,36 | 4 | 283,84 | 70,96 |
|
| Итого | 30 | 1320,54 | 213,669 |
Вывод. Анализ данных табл. 8 показывает, что с увеличением уровня производительности труда от группы к группе систематически возрастает и выпуск продукции в среднем по каждой группе организаций, что свидетельствует о наличии прямой корреляционной связи между исследуемыми признаками.
1б. Применение метода корреляционной таблицы.
Корреляционная таблица представляет собой комбинацию двух рядов распределения. Строки таблицы соответствуют группировке единиц совокупности по факторному признаку Х, а графы – группировке единиц по результативному признаку Y. На пересечении j-ой строки и k-ой графы указывается число единиц совокупности, входящих в j-ый интервал по факторному признаку и в k-ый интервал по результативному признаку. Концентрация частот около диагонали построенной таблицы свидетельствует о наличии корреляционной связи между признаками. Связь прямая, если частоты располагаются по диагонали, идущей от левого верхнего угла к правому нижнему. Расположение частот по диагонали от правого верхнего угла к левому нижнему говорит об обратной связи.
Для построения корреляционной таблицы необходимо знать величины и границы интервалов по двум признакам X и Y. Величина интервала и границы интервалов для факторного признака Х – Уровень производительности труда известны из табл. 8. Для результативного признака Y – Выпуск продукции величина интервала определяется по формуле (1) при k = 5, у max = 79,2 млн руб., у min = 14,4 млн руб.:
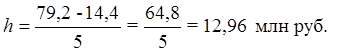
Границы интервалов ряда распределения результативного признака Y имеют следующий вид (табл. 9):
Таблица 9
| Номер группы | Нижняя граница, млн руб. | Верхняя граница, млн руб. |
| 1 | 14,4 | 27,36 |
| 2 | 27,36 | 40,32 |
| 3 | 40,32 | 53,28 |
| 4 | 53,28 | 66,24 |
| 5 | 66,24 | 79,2 |
Подсчитывая с использованием принципа полуоткрытого интервала [ ) число банков, входящих в каждую группу (частоты групп), получаем интервальный ряд распределения результативного признака (табл. 10).
Таблица 10
Распределение организаций по выпуску продукции
| Группы организаций по выпуску продукции, млн. руб., х | Число организаций, fj |
| 14,4 - 27,36 | 4 |
| 27,36 – 40,32 | 8 |
| 40,32 – 53,28 | 9 |
| 53,28 – 66,24 | 6 |
| 66,24 – 79,2 | 3 |
| Итого | 30 |
Используя группировки по факторному и результативному признакам, строим корреляционную таблицу (табл. 11).
Таблица 11
Корреляционная таблица зависимости выпуска продукции от уровня производительности труда
| Группы организаций по уровню производительности труда, млн руб./чел. | Группы организаций по выпуску продукции, млн. руб. | |||||
| 14,4 - 27,36 | 27,36 - 40,32 | 40,32 – 53,28 | 53,28 – 66,24 | 66,24 – 79,2 | Итого | |
| 0,12 – 0,168 | 3 |
|
|
|
|
|
| 0,168 – 0,216 | 1 | 3 |
|
|
|
|
| 0,216 – 0,264 | 5 | 7 |
|
|
| |
| 0,264 – 0,312 |
| 2 | 5 |
|
| |
| 0,312 – 0,36 |
|
| 1 | 3 |
| |
| Итого | 4 | 8 | 9 | 6 | 3 | 30 |
Вывод. Анализ данных табл. 11 показывает, что распределение частот групп произошло вдоль диагонали, идущей из левого верхнего угла в правый нижний угол таблицы. Это свидетельствует о наличии прямой корреляционной связи между уровнем производительности труда и выпуском продукции.
2. Измерение тесноты корреляционной связи с использованием коэффициента детерминации и эмпирического корреляционного отношения
Для измерения тесноты связи между факторным и результативным признаками рассчитывают специальные показатели – эмпирический коэффициент детерминации 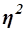 и эмпирическое корреляционное отношение
и эмпирическое корреляционное отношение 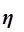 .
.
Эмпирический коэффициент детерминации 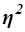 оценивает, насколько вариация результативного признака Y объясняется вариацией фактора Х (остальная часть вариации Y объясняется вариацией прочих факторов). Показатель
оценивает, насколько вариация результативного признака Y объясняется вариацией фактора Х (остальная часть вариации Y объясняется вариацией прочих факторов). Показатель 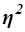 рассчитывается как доля межгрупповой дисперсии в общей дисперсии по формуле
рассчитывается как доля межгрупповой дисперсии в общей дисперсии по формуле
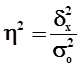 , (9)
, (9)
где 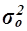 – общая дисперсия признака Y,
– общая дисперсия признака Y,
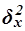 – межгрупповая (факторная) дисперсия признака Y.
– межгрупповая (факторная) дисперсия признака Y.
Значения показателя 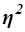 изменяются в пределах
изменяются в пределах 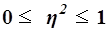 . При отсутствии корреляционной связи между признаками Х и Y имеет место равенство
. При отсутствии корреляционной связи между признаками Х и Y имеет место равенство 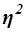 =0, а при наличии функциональной связи между ними - равенство
=0, а при наличии функциональной связи между ними - равенство 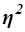 =1.
=1.
Общая дисперсия 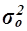 характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на Y факторов (систематических и случайных). Этот показатель вычисляется по формуле
характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на Y факторов (систематических и случайных). Этот показатель вычисляется по формуле
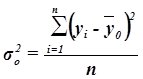 , (10)
, (10)
где yi – индивидуальные значения результативного признака;
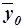 – общая средняя значений результативного признака;
– общая средняя значений результативного признака;
n – число единиц совокупности.
Общая средняя 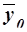 вычисляется как средняя арифметическая простая по всем единицам совокупности:
вычисляется как средняя арифметическая простая по всем единицам совокупности:
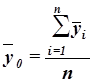 (11)
(11)
или как средняя взвешенная по частоте групп интервального ряда:
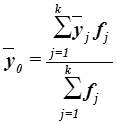 (12)
(12)
Для вычисления 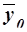 удобно использовать формулу (11), т.к. в табл. 8 (графы 3 и 4 итоговой строки) имеются значения числителя и знаменателя формулы.
удобно использовать формулу (11), т.к. в табл. 8 (графы 3 и 4 итоговой строки) имеются значения числителя и знаменателя формулы.
Расчет 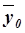 по формуле (11):
по формуле (11):
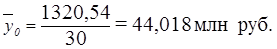
Для расчета общей дисперсии 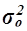 применяется вспомогательная таблица 12.
применяется вспомогательная таблица 12.
Таблица 12
Вспомогательная таблица для расчета общей дисперсии
| Номер организации п/п | Выпуск продукции, млн руб. | 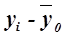
| 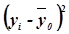
| 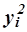
|
| 1 | 2 | 3 | 4 | 5 |
| 1 | 36,45 | -7,568 | 57,274 | 1328,602 |
| 2 | 23,4 | -20,618 | 425,101 | 547,56 |
| 3 | 46,54 | 2,522 | 6,360 | 2165,971 |
| 4 | 59,752 | 15,734 | 247,558 | 3570,301 |
| 5 | 41,415 | -2,603 | 6,775 | 1715,202 |
| 6 | 26,86 | -17,158 | 294,396 | 721,459 |
| 7 | 79,2 | 35,182 | 1237,773 | 6272,64 |
| 8 | 54,72 | 10,702 | 114,532 | 2994,278 |
| 9 | 40,424 | -3,594 | 12,916 | 1634,099 |
| 10 | 30,21 | -13,808 | 190,660 | 912,644 |
| 11 | 42,418 | -1,6 | 2,56 | 1799,286 |
| 12 | 64,575 | 20,557 | 422,590 | 4169,930 |
| 13 | 51,612 | 7,594 | 57,668 | 2663,798 |
| 14 | 35,42 | -8,598 | 73,925 | 1254,576 |
| 15 | 14,4 | -29,618 | 877,225 | 207,36 |
| 16 | 36,936 | -7,082 | 50,154 | 1364,268 |
| 17 | 53,392 | 9,374 | 87,871 | 2850,705 |
| 18 | 41 | -3,018 | 9,108 | 1681 |
| 19 | 55,68 | 11,662 | 136,002 | 3100,262 |
| 20 | 18,2 | -25,818 | 666,569 | 331,24 |
| 21 | 31,8 | -12,218 | 149,279 | 1011,240 |
| 22 | 39,204 | -4,814 | 23,174 | 1536,953 |
| 23 | 57,128 | 13,11 | 171,872 | 3263,608 |
| 24 | 28,44 | -15,578 | 242,674 | 808,833 |
| 25 | 43,344 | -0,674 | 0,454 | 1878,702 |
| 26 | 70,72 | 26,702 | 712,996 | 5001,318 |
| 27 | 41,832 | -2,186 | 4,778 | 1749,916 |
| 28 | 69,345 | 25,327 | 641,456 | 4808,729 |
| 29 | 35,903 | -8,115 | 65,853 | 1289,025 |
| 30 | 50,22 | 6,202 | 38,464 | 2522,048 |
| Итого | 1320,54 | 0 | 7028,017 | 65155,553 |
Расчет общей дисперсии по формуле (10):
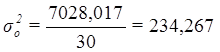
Общая дисперсия может быть также рассчитана по формуле
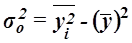 ,
,
где 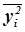 – средняя из квадратов значений результативного признака,
– средняя из квадратов значений результативного признака,
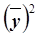 – квадрат средней величины значений результативного признака.
– квадрат средней величины значений результативного признака.
Для демонстрационного примера
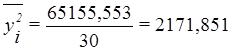
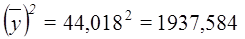
Тогда
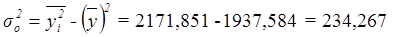
Межгрупповая дисперсия 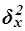 измеряет систематическую вариацию результативного признака, обусловленную влиянием признака-фактора Х (по которому произведена группировка). Воздействие фактора Х на результативный признак Y проявляется в отклонении групповых средних
измеряет систематическую вариацию результативного признака, обусловленную влиянием признака-фактора Х (по которому произведена группировка). Воздействие фактора Х на результативный признак Y проявляется в отклонении групповых средних 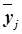 от общей средней
от общей средней 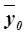 . Показатель
. Показатель 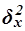 вычисляется по формуле
вычисляется по формуле
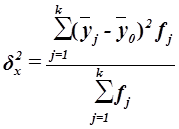 , (13)
, (13)
где 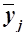 –групповые средние,
–групповые средние,
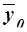 – общая средняя,
– общая средняя,
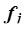 –число единиц в j-ой группе,
–число единиц в j-ой группе,
k – число групп.
Для расчета межгрупповой дисперсии 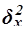 строится вспомогательная таблица 13 При этом используются групповые средние значения
строится вспомогательная таблица 13 При этом используются групповые средние значения 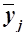 из табл. 8 (графа 5).
из табл. 8 (графа 5).
Таблица 13
Вспомогательная таблица для расчета межгрупповой дисперсии
| Группы организаций по уровню производительности труда | Число организаций,
| Среднее значение | 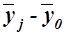
|
|
| 1 | 2 | 3 | 4 | 5 |
| 0,12 – 0,168 | 3 | 18,666 | -25,352 | 1928,171 |
| 0,168 – 0,216 | 4 | 29,327 | -14,691 | 863,301 |
| 0,216 – 0,264 | 12 | 40,073 | -3,945 | 186,756 |
| 0,264 – 0,312 | 7 | 54,643 | 10,625 | 790,234 |
| 0,312 – 0,36 | 4 | 70,96 | 26,942 | 2903,485 |
| Итого | 30 |
| 6671,947 |
Расчет межгрупповой дисперсии 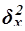 по формуле (11):
по формуле (11):
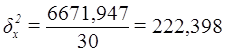
Расчет эмпирического коэффициента детерминации 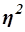 по формуле (9):
по формуле (9):
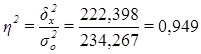 или 94,9%
или 94,9%
Вывод. 94,9% вариации выпуска продукции организаций обусловлено вариацией уровня производительности труда, а 5,1% – влиянием прочих неучтенных факторов.
Эмпирическое корреляционное отношение 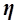 оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле
оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле
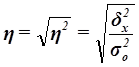 (14)
(14)
Значение показателя изменяются в пределах 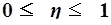 . Чем ближе значение
. Чем ближе значение 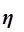 к 1, тем теснее связь между признаками. Для качественной оценки тесноты связи на основе
к 1, тем теснее связь между признаками. Для качественной оценки тесноты связи на основе 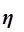 служит шкала Чэддока (табл. 14):
служит шкала Чэддока (табл. 14):
Таблица 14
Шкала Чэддока
| h | 0,1 – 0,3 | 0,3 – 0,5 | 0,5 – 0,7 | 0,7 – 0,9 | 0,9 – 0,99 |
| Характеристика силы связи | Слабая | Умеренная | Заметная | Тесная | Весьма тесная |
Расчет эмпирического корреляционного отношения 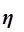 по формуле (14):
по формуле (14):
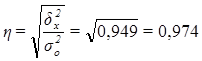 или 97,4%
или 97,4%
Вывод. Согласно шкале Чэддока связь между уровнем производительности труда и выпуском продукции организаций является весьма тесной.
Задание 3
По результатам выполнения Задания 1 с вероятностью 0,954 необходимо определить:
1) ошибку выборки среднего уровня производительности труда и границы, в которых будет находиться производительность труда в генеральной совокупности.
2) ошибку выборки доли организаций с уровнем производительности труда 0,264 млн руб./чел и более, а также границ, в которых будет находиться генеральная доля.
Выполнение Задания 3
Целью выполнения данного Задания является определение для генеральной совокупности организаций региона границ, в которых будут находиться величина среднего уровня производительности труда организаций и доля организаций с уровнем производительности труда не менее 0,264 млн руб./чел.
1. Определение ошибки выборки среднего уровня производительности труда организаций и границы, в которых будет находиться генеральная совокупность.
Применение выборочного метода наблюдения всегда связано с установлением степени достоверности оценок показателей генеральной совокупности, полученных на основе значений показателей выборочной совокупности. Достоверность этих оценок зависит от репрезентативности выборки, т.е. от того, насколько полно и адекватно представлены в выборке статистические свойства генеральной совокупности. Как правило, генеральные и выборочные характеристики не совпадают, а отклоняются на некоторую величину ε, которую называют ошибкой выборки (ошибкой репрезентативности).
Значения признаков единиц, отобранных из генеральной совокупности в выборочную, всегда случайны, поэтому и статистические характеристики выборки случайны, следовательно, и ошибки выборки также случайны. Ввиду этого принято вычислять два вида ошибок - среднюю 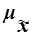 и предельную
и предельную 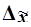 .
.
Средняя ошибка выборки 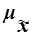 - это среднее квадратическое отклонение всех возможных значений выборочной средней от генеральной средней, т.е. от своего математического ожидания M[
- это среднее квадратическое отклонение всех возможных значений выборочной средней от генеральной средней, т.е. от своего математического ожидания M[ 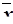 ].
].
Величина средней ошибки выборки рассчитывается дифференцированно (по различным формулам) в зависимости от вида и способа отбора единиц из генеральной совокупности в выборочную.
Для собственно-случайной и механической выборки с бесповторным способом отбора средняя ошибка 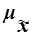 выборочной средней
выборочной средней 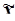 определяется по формуле
определяется по формуле
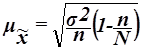 , (15)
, (15)
где 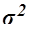 – общая дисперсия выборочных значений признаков,
– общая дисперсия выборочных значений признаков,
N – число единиц в генеральной совокупности,
n – число единиц в выборочной совокупности.
Предельная ошибка выборки 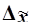 определяет границы, в пределах которых будет находиться генеральная средняя:
определяет границы, в пределах которых будет находиться генеральная средняя:
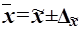 ,
,
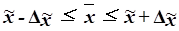 , (16)
, (16)
где 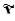 – выборочная средняя,
– выборочная средняя,
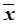 – генеральная средняя.
– генеральная средняя.
Границы задают доверительный интервал генеральной средней, т.е. случайную область значений, которая с вероятностью Р гарантированно содержит значение генеральной средней. Эту вероятность Р называют доверительной вероятностью или уровнем надёжности.
В экономических исследованиях чаще всего используются доверительные вероятности Р= 0.954, Р= 0.997, реже Р= 0,683.
В математической статистике доказано, что предельная ошибка выборки Δ кратна средней ошибке µ с коэффициентом кратностиt (называемым также коэффициентом доверия), который зависит от значения доверительной вероятности Р. Для предельной ошибки выборочной средней 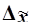 это теоретическое положение выражается формулой
это теоретическое положение выражается формулой
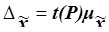 (17)
(17)
Значения t вычислены заранее для различных доверительных вероятностей Р и протабулированы (таблицы функции Лапласа Ф). Для наиболее часто используемых уровней надежности Р значения t задаются следующим образом (табл. 15):
Таблица 15
| Доверительная вероятность P | 0,683 | 0,866 | 0,954 | 0,988 | 0,997 | 0,999 |
| Значение t | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 |
По условию задачи выборочная совокупность насчитывает 30 организаций, выборка 20% механическая, следовательно, генеральная совокупность включает 150 организаций. Выборочная средняя 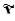 , дисперсия
, дисперсия 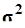 определены в Задании 1 (п. 3). Значения параметров, необходимых для решения задачи, представлены в табл. 16:
определены в Задании 1 (п. 3). Значения параметров, необходимых для решения задачи, представлены в табл. 16:
Таблица 16
Р | t | n | N | 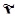
| 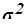
|
| 0,954 | 2 | 30 | 150 | 0,248 | -,0028 |
Расчет средней ошибки выборки по формуле (15):
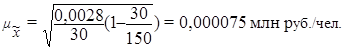 ,
,
Расчет предельной ошибки выборки по формуле (17):
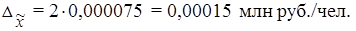
Определение по формуле (16) доверительного интервала для генеральной средней:
0,248-0,00015 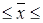 0,248+0,00015
0,248+0,00015
0,24785 млн руб./чел. 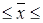 0,24815 млн руб.
0,24815 млн руб.
Вывод. На основании проведенного выборочного обследования организаций региона с вероятностью 0,954 можно утверждать, что для генеральной совокупности организаций средний уровень производительности труда находится в пределах от ,024785 млн руб./чел. до 0,24815 млн руб./чел.
3. Определение ошибки выборки доли организаций с уровнем производительности труда 0,264 млн руб./чел и более, а также границ, в которых будет находиться генеральная доля.
Доля единиц выборочной совокупности, обладающих тем или иным заданным свойством, выражается формулой
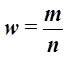 , (18)
, (18)
где m – число единиц совокупности, обладающих заданным свойством;
n – общее число единиц в совокупности.
Для собственно-случайной и механической выборки с бесповторным способом отбора предельная ошибка выборки 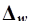 доли единиц, обладающих заданным свойством, рассчитывается по формуле
доли единиц, обладающих заданным свойством, рассчитывается по формуле
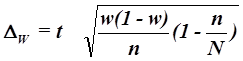 , (19)
, (19)
где w – доля единиц совокупности, обладающих заданным свойством;
(1- w ) – доля единиц совокупности, не обладающих заданным свойством,
N – число единиц в генеральной совокупности,
n– число единиц в выборочной совокупности.
Предельная ошибка выборки 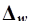 определяет границы, в пределах которых будет находиться генеральная доля р единиц, обладающих заданным свойством:
определяет границы, в пределах которых будет находиться генеральная доля р единиц, обладающих заданным свойством:
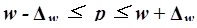 (20)
(20)
4. По условию Задания 3 исследуемым свойством является равенство или превышение уровня производительности труда величины 0,264 млн руб./чел.
Число организаций с заданным свойством определяется из табл. 3 (графа 3):
m=11
Расчет выборочной доли по формуле (18):
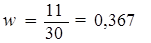
Расчет по формуле (19) предельной ошибки выборки для доли:
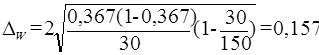
Определение по формуле (20) доверительного интервала генеральной доли:
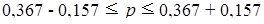
0,21 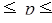 0,524
0,524
или
21% 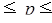 52,4%
52,4%
5. Вывод. С вероятностью 0,954 можно утверждать, что в генеральной совокупности организаций доля организаций с уровнем производительности труда 0,264 млн руб./чел. и выше будет находиться в пределах от 21% до 52,4%.
Задание 4
По исходным данным табл. 17 необходимо выполнить следующее:
1. Определить уровни среднечасовой, среднедневной и среднегодовой производительности труда, их динамику и взаимосвязь. Расчеты представить в таблице.
2. Определить абсолютный прирост среднегодовой производительности труда одного работника за счет отдельных факторов (среднечасовой производительности труда рабочего, средней продолжительности рабочего дня, и рабочего года, доли рабочих в общей численности работников).
Сделать выводы по результатам выполнения Задания 4.
Таблица 17
Имеются следующие данные по организации за два года:
| № п/п | Показатели | Базисный год | Отчетный год |
| 1. | Выпуск продукции (в сопоставимых ценах), млн.руб. | 40,8 | 54,2 |
| 2. | Среднесписочная численность работников, чел. | 164 | 180 |
| 3. | В том числе рабочих, чел. | 130 | 145 |
| 4. | Отработано рабочими чел.-дней | 31200 | 33060 |
| 5. | Отработано рабочими чел.-ч | 240 240 | 261 174 |
Выполнение Задания 4.
Часть.
· Средняя часовая выработка отражает результаты труда одного
рабочего за час фактической работы. Она равна отношению объема произведенной продукции к числу человеко-часов, фактически отработанных в течение данного периода времени
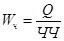
· Средняя дневная выработка. Она равна отношению объема
произведенной продукции к числу человеко-дней, фактически отработанных всеми рабочими предприятиями.
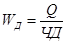
· Средняя выработка за период времени (среднемесячная, среднеквартальная, среднегодовая) одного списочного рабочего или работника всего персонала, непосредственно связанного с производством данной продукции (промышленно-производственного персонала). Она равна отношению объема продукции к среднесписочной численности рабочих (ТР) или работников промышленно - производственного персонала (ТППП) соответственно.
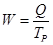
или
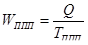
1.Средняя часовая выработка:
- Базисный период
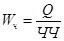 = 40,8 / 240240 = 0,0001 млн.руб.
= 40,8 / 240240 = 0,0001 млн.руб.
- Отчетный период
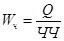 = 54,2 / 240240 = 0,0002 млн.руб.
= 54,2 / 240240 = 0,0002 млн.руб.
2.Средняя дневная выработка.
- Базисный период
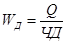 = 40,8 / 31200 = 0,0013 млн.руб.
= 40,8 / 31200 = 0,0013 млн.руб.
- Отчетный период
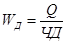 = 54,2 / 33060 = 0,0016 млн.руб.
= 54,2 / 33060 = 0,0016 млн.руб.
3. Средняя выработка за год одного списочного рабочего
- Базисный период
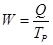 = 40,8 / 164 = 0,2488 млн. руб.
= 40,8 / 164 = 0,2488 млн. руб.
- Отчетный период
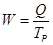 = 54,2 / 180 = 0,3011 млн. руб.
= 54,2 / 180 = 0,3011 млн. руб.
4. Средняя выработка за год работника всего персонала, непосредственно связанного с производством данной продукции
- Базисный период
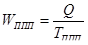 = 40,8 / 130 = 0,3138 млн.руб.
= 40,8 / 130 = 0,3138 млн.руб.
- Отчетный период
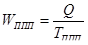 = 54,2 / 145 = 0,3738 млн.руб.
= 54,2 / 145 = 0,3738 млн.руб.
Дата: 2019-12-22, просмотров: 342.
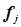
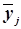 в группе
в группе