В малой окрестности точки изображения интенсивность должна оставаться большой, так как разность хода и разность фаз при изменении точки наблюдения меняются непрерывно, а не скачком. Это приводит к тому, что на экране изображение точечного источника света — не точка, а маленький светлый кружок. На границах кружка расфазировка дифрагированных волн становится порядка 2p. Размер этого кружка можно формально найти, если представить себе, что линза, как дырка в экране, приводит к дифракции на круглом отверстии. При дифракции плоской волны на круглом отверстии основная часть света идет в угол порядка l/D, где D — диаметр линзы. Угловой радиус первого темного кольца равен 0.61×l/D. Оказывается, что эта дифракционная расходимость не может быть скомпенсирована преломлением по законам геометрической оптики ни на какой сложной поверхности линзы. Поэтому плоская волна, например, собирается за линзой не в одну точку, а в кружок с радиусом 0.61×(l/D)×f, где f — фокусное расстояние линзы.

     Если сопряженная источнику света плоскость не совпадает с фокальной плоскостью линзы и находится на расстоянии L, то дифракционный радиус r кружка изображения точечного источника можно найти по формуле

r = 0.61× 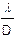×L.

     Это основная формула, используемая при решении задач по теме "Дифракционный предел разрешения". Так, предел углового разрешения телескопа связан с тем, что изображение далекой звезды в фокальной плоскости линзы представляет собой кружок, а не точку. Принято считать (критерий Рэлея), что две звезды будут видны как две, если центр кружка изображения одной звезды совпадает с первым темным кольцом дифракционного изображения второй звезды. В качестве задачи можете доказать, что это выполняется при угловом расстоянии между звездами, равном 0.61×l/D. Это и есть предел углового разрешения телескопа.

     Аналогично примерно величине l/D равен предел углового разрешения глаза и микроскопа. Для микроскопа обычно вместо углового разрешения рассматривают линейное разрешение l_min — наименьшее расстояние между двумя "деталями" предмета, при котором микроскоп позволяет определить, что "детали" две, а не одна. Каждая мелкая "деталь" на экране вместо точки дает дифракционный кружок изображения. Если этот кружок по законам геометрической оптики отобразить на предмет, то его размер и будет примерно равен разрешению микроскопа l_min. Предмет в микроскопе находится примерно на фокусном расстоянии f от объектива, угловое дифракционное разрешение которого l/D. Следовательно,

l_min = f×  = ,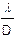

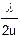где 2u — входная апертура объектива.

     Если между предметом и объективом среда с показателем преломления n, то длина волны в среде в n раз меньше, поэтому

l_min = .

     Более строгая теория для некогерентного освещения объекта дает выражение

l_min = .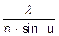

Величину n×sin u называют числовой апертурой.

     Явление дифракции также ограничивает спектральное разрешение спектрометра. Вспомните нормальную ширину щели.

     Во всех случаях явление дифракции ограничивает угловое разрешение прибора величиной порядка l/D, где D — ширина пучка лучей.

ЗАКЛЮЧЕНИЕ

     В заключение сделаем несколько замечаний о полезности применения соображений размерности.

     Многие соотношения в оптике, как и вообще в физике, могут быть получены путем построения простейшей зависимости требуемых величин с учетом необходимой размерности результата.

     Всевозможные малые углы можно выразить как отношение двух длин, одна из которых — длина волны l, если угол зависит от нее. Так, угол дифракции равен l/D, где D — размер препятствия; максимальная апертура интерференции — l/b, где b — размер источника света; угловой размер источника света — l/L_^ , где L_^ — длина пространственной когерентности; угол, под которым интерферирующие лучи сходятся на экране — l/d, где d — ширина полос интерференции.

     Дифракционная решетка имеет три характерных линейных размера: a — ширина прозрачной части штриха, d — шаг решетки, Nd — полная ширина решетки. Им соответствуют три характерных угла: l/a — направление нулевой интенсивности дифракции на одной щели; l/d — угол между главными максимумами дифракции; l/(Nd)— угловая ширина главного максимума.

     Частота и время — величины обратные. Обратная частота — это период колебаний 1/n = T; единица, деленная на спектральную ширину, — время когерентности 1/dn = t; если излучение состоит из двух близких частот, то 1/(n₁-n₂) — период биений.

     Если в зависимости сигнала от времени есть особенность с характерным временем T, то в спектре сигнала есть особенность размером 1/T. Если свет встречает особенность с характерным линейным размером D, то в распределении света по углам появляется особенность размером l/D. И вообще, распределение света по углам — Фурье–образ препятствия.

     Подробнее см. литературу [2, 3].

Л и т е р а т у р а

     1. Козел С.М., Рашба Э.И., Славатинский С.А. Сборник задач по физике: Учеб. пособие. – М.: Наука, 1987.– 304с.

     2. Бутиков Е.И. Оптика: Учеб. пособие для вузов/ Под ред. Н.И. Калитеевского. – М.: Высш. шк., 1986.– 512с.

     3. Борн М., Вольф Э. Основы оптики. - М.: Наука, 1973.– 720с.

С О Д Е Р Ж А Н И Е

КРАТКАЯ СВОДКА ОСНОВНЫХ ФОРМУЛ . . . . . . . . . . 1 ГЕОМЕТРИЧЕСКАЯ ОПТИКА . . . . . . . . . . . . . . . . . . 8      Направление распространения света . . . . . . . . . . . . . 8 Световые лучи . . . . . . . . . . . . . . . . . . . . . . . . . 8 Приближение геометрической оптики . . . . . . . . . . . . 8 Отражение и преломление света . . . . . . . . . . . . . . . 9 Отражение от плоского зеркала . . . . . . . . . . . . . . . . 9 Призма . . . .  . . . . . . . . . . . . . . . . . . . . . . . . . 10 Оптическая ось . . . . . . . . . . . . . . . . . . . . . . . . . 10 Линза . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 Построение изображений . . . . . . . . . . . . . . . . . . 11 Построение изображения в тонкой линзе . . . . . . . . . 12 Построение изображения в толстой линзе . . . . . . . . . 14 Формулы тонкой линзы . . . . . . . . . . . . . . . . . . . 15 Сферическое зеркало . . . . . . . . . . . . . . . . . . . . . 16 Глаз . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 Фотоаппарат . . . . . . . . . . . . . . . . . . . . . . . . . 17    Окуляр . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 Подзорная труба, телескоп . . . . . . . . . . . . . . . . . 18 Микроскоп . . . . . . . . . . . . . . . . . . . . . . . . . . 20   Шкала, крест, острие . . . . . . . . . . . . . . . . . . . . . 21 Спектрометр . . . . . . . . . . . . . . . . . . . . . . . . . . 21 ФОТОМЕТРИЯ . . . . . . . . . . . . . . . . . . . . . . . . . . . 23   Основные понятия волновой оптики . . . . . . . . . .  . . . 25     ИНТЕРФЕРЕНЦИЯ . . . . . . . . . . . . . . . . . . . . . . 28   Поляризатор . . . . . . . . . . . . . . . . . . . . . . . . 28   Пластинки l/2 и l/4 . . . . . . . . . . . . . . . . . . . . 29     Двухлучевая интерференция . . . . . . . . . . . . . . . . . 30   Оптическая разность хода . . . . . . . . . . . . . . . . . 31   Ширина интерференционных полос . . . . . . . . . . . . 32     Потеря полуволны . . . . . . . . . . . . . . . . . . . . . 34   Интерференция и закон сохранения энергии . . . . . . . 34   Частично когерентный свет . . . . . .  . . . . . . . . . . 36   Квазимонохроматический свет . . . . . . . . . . . . . . 37   Порядок интерференции . . . . . . . . . . . . . . . . . . 38   Область высокой видности интерференционной                        картины при квазимонохроматическом источнике света 39   Временная когерентность . . . . . . . . . . . . . . . . . . . 40   Пространственная когерентность . . . . . . . . . . . . . 41        Видность интерференционной картины                                                            с протяженным источником света . . . . . . . . . . . 42   Связь пространственной когерентности и                                                        углового размера источника света . . . . . . . . . . 43     Апертура интерференции . . . . . . . . . . . . . . . . . . 43   Объем когерентности . . . . . . . . . . . . . . . . . . . . 44   Совместное влияние временной и пространственной                                   когерентности на интерференционную картину . . . 45   Локализация интерференционной картины . . . . . . . . 45       Полосы равной толщины и полосы равного наклона . . . 47 ДИФРАКЦИЯ . . . . . . . . . . . . . . . . . . . . . . . . . . . 48        Комплексная амплитуда световой волны . . . . . . . . . . 49     Ключевые моменты решения задач по теме "дифракция" 51       Дифракция на одной щели . . . . . . . . . . . . . . . . . . 52   Дифракционная решетка . . . . . . . . . . . . . . . . . . 55   Зоны Френеля . . . . . . . . . . . . . . . . . . . . . . . . . 58   Дифракция Фраунгофера . . . . . . . . . . . . . . . . . 62   Дифракция Френеля . . . . . . . . . . . . . . . . . . . . . 62   Сравнение линзы и зонной пластинки . . . . . . . . . . . . 62   Дифракционный предел разрешения . . . . . . . . . . . . 63    ЗАКЛЮЧЕНИЕ . . . . . . . . . . . . . . . . . . . . . . . 65    ЛИТЕРАТУРА . . . . . . . . . . . . . . . . . . . . . . . . . . . 66