Обычно экран для наблюдения интерференционной картины располагают так, чтобы оба луча и нормаль к экрану находились в одной плоскости. В этом случае ширина интерференционных полос полностью определяется углами падения световых волн на экран и длиной световой волны и не зависит от оптической схемы формирования интерферирующих волн.

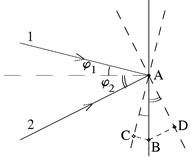
     Пусть две плоские световые волны падают на экран под углами j₁ и j₂ (рис. 18), точки A и B — середины двух соседних светлых полос на экране, AC — поверхность равной фазы первой волны, AD — поверхность равной фазы второй волны. Поверхность AC имеет ту же фазу, что и поверхность AD, так как в точке A фазы двух волн одинаковые (светлая полоса). Поэтому можно считать, что это одна и та же поверхность равной фазы волны, идущей от одного точечного источника разными путями. Следовательно, оптическую разность хода, например для точки экрана B, можно отсчитывать от пары точек C и D как бы общей поверхности равной фазы.

     Из рис. 18 видно, что поверхность равной фазы AC первой волны еще не дошла до точки B на отрезок CB, а поверхность AD второй волны уже зашла за точку B на отрезок BD. Тогда оптическая разность хода D для точки B равна

D = CB+BD =

= AB×sin j₁ + AB×sin j₂ = AB×(sin j₁ + sin j₂).

     Точки A и B — середины соседних светлых полос, тогда оптическая разность хода равна длине волны D = l, так как при переходе по экрану на одну полосу разность хода меняется на l. Выразив из этого равенства ширину полосы AB и обозначив ее через d, получаем

d = AB =  = ,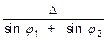

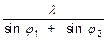где знак '+' соответствует положительным углам падения j₁ и j₂ отсчитанным в разные стороны от нормали к экрану, как на рис.18.

     В большинстве задач углы падения малы, тогда sin j » j и выражение для ширины полос упрощается

d = ,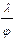

где j = j₁+j₂ — угол между лучами, сходящимися на экране.

     Эта формула сводит оптическую задачу к геометрической. Для определения ширины интерференционных полос нужно построить два луча, выходящие из одной точки источника света и попадающие в одну точку экрана. Ширина полос — это отношение длины волны света к углу между лучами, сходящимися в одну точку.

     Если ширины соседних полос заметно различаются, то термина "ширина полос" избегают. Такая ситуация возникает при интерференции плоской и сферической волн, например при наблюдении колец Ньютона. Кольца Ньютона наблюдаются при интерференции волны, отраженной от сферической поверхности выпуклой линзы, и волны, отраженной от плоской поверхности, соприкасающейся со сферической поверхностью линзы. В этой задаче вместо ширины полос ищут радиус светлого (или темного) кольца с произвольным номером k.

Потеря полуволны

     В соответствии с формулами Френеля [2, 3] на границе раздела двух сред преломленная световая волна всегда в фазе с падающей волной, отраженная волна — либо в фазе, либо в противофазе. Иной сдвиг фазы отраженной волны возникает только в случае полного внутреннего отражения.

     При нормальном падении света на границу раздела двух сред отраженная волна в точке падения будет в противофазе с падающей при отражении от оптически более плотной среды, от среды с более высоким показателем преломления. Противоположная фаза отраженной волны эквивалентна сдвигу фазы на p, или изменению разности хода на l/2. Поэтому говорят, что при отражении от оптически более плотной среды происходит потеря полуволны. При этом в выражении для оптической длины пути следует добавить (или вычесть) слагаемое l/2.

     Если одна из интерферирующих волн по пути к экрану испытала отражение с потерей полуволны, как, например, при наблюдении колец Ньютона в отраженном свете, то без учета потери полуволны в рассчитанной интерференционной картине темные полосы окажутся на месте светлых, а светлые — на месте темных.