Пусть напряженность электрического поля E световой волны в некоторой точке изменяется по закону
E = E0×cos(wt-j).
Поставим в соответствие этой вещественной функции E некоторую комплексную функцию E’, которую будем называть комплексной напряженностью поля световой волны:
E’ = E0×exp{-i×(wt-j)},
где i — мнимая единица, а знак минус перед i — вопрос соглашения. Назовем величину E0×exp(i×j) — комплексной амплитудой световой волны.
Вещественная (настоящая) напряженность поля световой волны E равна вещественной части придуманной нами комплексной напряженности E’.
Возникает вопрос, насколько однозначно это сопоставление.
Действительно, есть неоднозначность сопоставления комплексного числа вещественному, но для аналитической функции, например гармонической (косинусоидальной), эта неоднозначность пропадает. Если вещественная функция в окрестности некоторой точки разлагается в ряд Тейлора, то эту функцию с помощью этого ряда однозначно можно продолжить на комплексную плоскость.
Зачем нужна комплексная напряженность поля?
Сложение комплексных напряженностей можно сделать наглядным. Комплексное число можно представить себе как вектор на комплексной плоскости и складывать комплексные напряженности по правилам сложения векторов. Сумма вещественных напряженностей может быть получена как вещественная часть суммы комплексных напряженностей.
Для монохроматического света (света одной частоты) можно складывать не комплексные напряженности, а комплексные амплитуды, так как одни от других отличаются одинаковым для всех слагаемых множителем exp(-iwt). Комплексная амплитуда суммы волн равна сумме комплексных амплитуд.
Складывая комплексные амплитуды волн, излучаемых вторичными источниками, мы можем найти комплексную амплитуду поля в любой точке за щелью. Длина этого вектора на комплексной плоскости равна амплитуде вещественного поля E, а направление определяет сдвиг фазы колебаний вещественного поля.
Все приемники света в оптическом диапазоне регистрируют интенсивность света, а не напряженность поля световой волны. Интенсивность света равна квадрату модуля комплексной амплитуды поля с коэффициентом c/8p в системе единиц СГС Гаусса для линейной поляризации света. Часто в задачах интересуются отношением интенсивностей, в этом случае постоянный сомножитель несуществен.
Итак, задача по дифракции обычно сводится к векторному сложению комплексных амплитуд вторичных источников света. От чего же зависят величины и фазы этих комплексных амплитуд?
Согласно дифракционной формуле Френеля–Кирхгофа [3] комплексная амплитуда вторичного источника света в точке наблюдения может быть выражена по формуле
dEp’ = 
×Es’× 
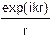×(cos q1 + cos q2)×dS.
Здесь Es’ — комплексная амплитуда поля в точке расположения вторичного источника света, dS — площадь излучающей поверхности вторичного источника, r — расстояние от вторичного источника до точки наблюдения, k = 2p/l — волновое число, q1 — угол между нормалью к поверхности вторичного источника и направлением распространения света к точке вторичного источника, q2 — угол между нормалью к поверхности вторичного источника и направлением от вторичного источника к точке наблюдения.
В задачах по дифракции зависимостью амплитуды поля от направления излучения вторичного источника света обычно пренебрегают, что справедливо для малых углов дифракции.
Амплитуда излучения вторичного источника обратно пропорциональна расстоянию от вторичного источника до точки наблюдения, но в задачах по дифракции и этой зависимостью обычно пренебрегают. Последнее связано с тем, что в приближении малых углов дифракции различные точки экрана почти одинаково удалены от вторичного источника. Поэтому в выражении для комплексной амплитуды оставляют быстро меняющийся сомножитель exp(ikr), заменяя медленно меняющийся с расстоянием сомножитель 1/r константой.
Амплитуда вторичного источника света пропорциональна площади источника. При решении задач это обычно учитывают так, что мысленно разбивают щель или другой вторичный источник на источники света одинаковой площади, считая при этом, что они излучают волны, которые в точке наблюдения имеют одинаковые амплитуды, но разные фазы. Тогда векторы комплексных амплитуд будут по–разному ориентированы на комплексной плоскости. Угол поворота относительно оси X равен фазе комплексного числа.
Фазовый множитель комплексной амплитуды равен exp{ik(r1+r2)}, где k = 2p/l — волновое число, r1 — расстояние от истинного источника до вторичного источника, r2 — расстояние от вторичного источника до точки наблюдения. Следовательно, угол поворота на комплексной плоскости равен k(r1+r2).
Ключевые моменты решения задач по теме "дифракция"
Обычно в задаче по теме "дифракция" требуется найти интенсивность дифрагированной волны в некоторой точке или в некотором направлении.
Интенсивность равна квадрату модуля комплексной амплитуды с коэффициентом c/8p.
Комплексную амплитуду можно найти как векторную сумму комплексных амплитуд световых волн, пришедших от разных частей щели или другого вторичного источника света. Части удобно брать одинаковой площади.
Сумма амплитуд — это сумма (интеграл) маленьких векторов равной длины (для равных площадей разбиения вторичного источника), но по–разному ориентированных.
Угол поворота каждого вектора относительно оси X на комплексной плоскости равен kr = 2pr/l, где r = r1 + r2.
В качестве примера рассмотрим дифракцию Фраунгофера на одной щели.
Дифракция на одной щели
Рассмотрим дифракцию плоской монохроматической волны на щели, плоскость которой перпендикулярна направлению распространения волны.
Все вторичные источники в плоскости щели имеют одинаковую фазу. Поэтому при вычислении фазы излучения в точке наблюдения на экране за щелью остается учесть разность фаз, которая "набегает" от щели до экрана. Будем считать, что экран находится далеко от щели, что соответствует дифракции Фраунгофера. Подробнее дифракция Фраунгофера обсуждается ниже.
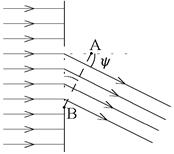
| Рис. 30 |
Если экран далеко, то можно считать, что точки на пунктирной прямой AB (рис. 30) одинаково удалены от точки наблюдения. Тогда для участка щели с координатой, равной y, расстояние до точки наблюдения равно y×sin y плюс несущественная константа.
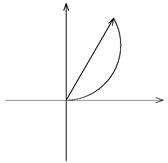
С изменением y—координаты линейно меняется расстояние до экрана, а значит — фаза поля, и угол поворота комплексной амплитуды на комплексной плоскости. Если мы мысленно разобьем щель на тонкие полоски одинаковой ширины dy, то одинаковые по модулю комплексные амплитуды от соседних полосок в точке наблюдения будут развернуты друг относительно друга на равные углы (2p/l)×dy×sin y. Складывая много маленьких векторов, мы получим картину их выстраивания в дугу окружности, так как одинаковы амплитуды векторов и одинаковы углы поворота между соседними векторами (рис. 31).
| Рис. 31 |
Векторная сумма — вектор, проведенный из начала первого вектора в конец последнего. Если суммируемые векторы образуют дугу окружности, то результирующий вектор — ее хорда.
Интенсивность равна квадрату длины этой хорды и не изменяется при повороте комплексных амплитуд на комплексной плоскости. Следовательно, интенсивность не зависит от общего поворота векторов на рис. 31. Поэтому ориентацию начального вектора суммы можно выбрать произвольно. Обычно первый вектор направляют вдоль оси X.
Обсудим, что изменится в картине сложения амплитуд на комплексной плоскости при изменении направления регистрации света.
Изменение угла y между направлением наблюдения и нормалью к плоскости щели приводит к изменению угла dj на комплексной плоскости между векторами комплексных амплитуд волн, пришедших в точку наблюдения от соседних участков щели:
dj = 
×dy×sin y.
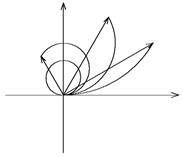
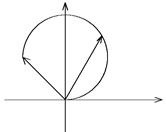
При сложении векторов на комплексной плоскости это приводит к изменению радиуса дуги окружности при сохранении длины дуги. Дуга несколько сворачивается или разворачивается (рис.32).
| Рис. 32 |
Длина дуги равна сумме модулей комплексных амплитуд волн, пришедших от разных участков щели, поэтому она сохраняется при изменении направления наблюдения y.
При условии y = 0 дуга окружности разворачивается в прямую линию, что соответствует максимуму дифракционной картины, а квадрат длины дуги определяет интенсивность света в максимуме.
При увеличении угла y наступает момент, когда амплитуда и интенсивность дифрагированного света равны нулю. Это происходит тогда, когда дуга (см. рис. 32) сворачивается в окружность, а длина хорды, соответственно, обращается в нуль. При этом фаза последнего суммируемого вектора отличается от фазы первого вектора на 2p, а разность хода от двух краев щели до точки наблюдения равна l. Следовательно, направление y нулевой интенсивности дифрагированной волны можно найти из равенства d×sin y = l, где d — полная ширина щели. Если y << 1, то y » l/d.
Большая часть энергии при дифракции на одной щели распространяется в угол 2l/d. Это угол между двумя направлениями на первый нуль интенсивности дифрагированной волны в обе стороны от центрального максимума. Полезно запомнить, что на щели свет дифрагирует примерно в угол l/d, так как для рассуждений "на пальцах" коэффициент 2 не имеет значения.
При дальнейшем увеличении угла дифракции y интенсивность после нулевого значения снова возрастает, так как длина дуги становится больше длины окружности, а амплитуда света равна хорде, проведенной из начала в конец дуги. Максимум амплитуды достигается, когда дуга сворачивается примерно в полторы окружности. Далее при увеличении угла y амплитуда и интенсивность снова убывают и обращаются в нуль при условии, что дуга сворачивается в две окружности: d×sin y = 2l и т.д.
Количественно решение задачи можно найти, если выразить квадрат длины хорды (интенсивность для текущего угла y) через квадрат длины дуги (интенсивность в максимуме) и угол, под которым дуга видна из центра окружности. Этот угол, как видно из рис. 32, равен разности фаз излучения от краев щели, которая в свою очередь равна (2p/l)×d×sin y. Оставшаяся часть решения задачи чисто геометрическая. В результате, интенсивность дифрагированного света выражается по формуле
I(y)=I(0)×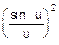 
,
где u = (p/l)×d×sin y.
Решение можно найти и другим путем, складывая комплексные амплитуды аналитически, а не геометрически. При этом надо складывать комплексные числа с одинаковыми амплитудами (пусть E0) и с разными фазами (2p/l)×y×sin y, где y — координата на щели текущего вторичного источника. Тогда суммарная амплитуда E’ может быть получена по формуле
E’ =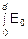 
×exp{i× 
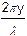×sin y}×dy.
Интенсивность связана с комплексной амплитудой соотношением I = (c/8p)×|E’|2. В окончательном выражении можно избавиться от параметра E0, используя вместо него I0 — интенсивность при y=0.
Что изменяется в картине сложения амплитуд на комплексной плоскости при изменении других параметров задачи?
Если изменять ширину щели при сохранении направления наблюдения, то изменяется длина дуги окружности при сохранении ее радиуса. Значения амплитуды дифрагированной волны для двух значений ширины щели приведены на рис. 33.
Если изменять интенсивность падающей волны, то картина сложения амплитуд дифрагированных волн будет меняться так, как изображено на рис. 34.
| Рис. 33 |
| Рис. 34 |
Дифракционная решетка
Рассмотрим простейшую дифракционную решетку, работающую на пропускание. Эта решетка представляет собой плоский экран с чередующимися прозрачными и непрозрачными полосами. Все прозрачные полосы имеют одинаковую ширину, скажем a. Все непрозрачные полосы также имеют одинаковую ширину — b. Сумма a+b = d называется шагом решетки. Общее число штрихов решетки обозначим N. Тогда ширина решетки равна произведению N×d.
Рассмотрим простейший случай дифракции плоской монохроматической волны, которая падает на решетку перпендикулярно ее плоскости, а распределение интенсивности дифрагированной волны нас будет интересовать на очень удаленном экране или, как говорят, на бесконечности.
Главный дифракционный максимум образуется при условии, что волны от соседних штрихов решетки приходят в точку наблюдения в одинаковой фазе или со сдвигом фаз, кратным 2p. Соответствующая разность хода должна быть кратна l:
d×sin y = ml,
где m — целое число. Это основная формула дифракционной решетки. Если угол падения света на решетку не равен нулю, то
d×(sin y1 + sin y2) = ml,
где y1 — угол падения, y2 — угол дифракции.
Какова амплитуда дифрагированной волны в том случае, если разность фаз волн от соседних штрихов мало отличается от величины, кратной 2p? Добавление к разности фаз величины, кратной 2p, не изменяет результат интерференции волн, поэтому будем считать, что разность фаз мало отличается от нуля. Амплитуда света от каждого штриха одна и та же. Разность фаз между волнами от соседних штрихов также одинакова. Число штрихов велико. Тогда картина сложения амплитуд на комплексной плоскости полностью аналогична картине сложения амплитуд при дифракции на одной щели. Векторы комплексных амплитуд будут лежать на дуге окружности.
При изменении направления наблюдения y дуга окружности будет несколько сворачиваться или разворачиваться в дугу меньшего или большего радиуса при сохранении длины дуги.
Направление главного максимума соответствует условию, когда дуга разворачивается в прямую линию.
Если дуга сворачивается в окружность, то интенсивность света в этом направлении равна нулю. При этом разность фаз волн от первого и последнего штрихов решетки равна 2p. Следовательно, разность фаз волн двух соседних штрихов равна 2p/N, что в N раз меньше разности фаз, соответствующей следующему главному максимуму.
Таким образом, ширина главного максимума примерно в N раз меньше расстояния между главными максимумами, где N — число штрихов решетки. Это соотношение полезно помнить при решении задач.
Если мы рассматриваем главный максимум с номером m, то угол, соответствующий направлению на главный максимум, примерно в mN раз больше угловой ширины главного максимума. Отсюда следует выражение для относительного спектрального разрешения решетки в m–м порядке дифракции:
= 
.
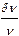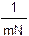Эта формула часто используется при решении задач.
Мы выяснили, что при изменении угла дифракции y от значения угла, соответствующего главному максимуму, до некоторого близкого значения, при котором интенсивность дифрагированной волны обращается в нуль, картина сложения амплитуд изменяется от прямой линии до окружности. Что происходит при дальнейшем изменении угла y?
Дуга сворачивается дальше, а когда она превращается в полторы окружности, суммарная амплитуда достигает более "мелкого" максимума. Это так называемый побочный максимум. Следующий побочный максимум появится, когда дуга свернется в две с половиной окружности и т.д.
В качестве задачи можно определить, сколько побочных максимумов между двумя главными максимумами и как зависит отношение амплитуды побочного максимума к амплитуде главного максимума от номера побочного максимума.
Обсудим теперь, какова амплитуда волны в направлении главного максимума. Эта амплитуда равна произведению числа штрихов решетки на амплитуду волны, дифрагированной в данном направлении от одного штриха.
Оказывается, при некоторых условиях амплитуда главного максимума может оказаться равной нулю. Эта ситуация может обыгрываться в задачах.
В первом порядке дифракции амплитуда главного максимума не может быть равна нулю, поэтому рассмотрим второй порядок дифракции. Во втором порядке разность хода от соседних штрихов равна 2l, что соответствует разности фаз 4p, которая "набегает" при перемещении по вторичным источникам света поперек штрихов от начала одного штриха до начала соседнего штриха.
Разность фаз 4p соответствует двум окружностям дуги сложения амплитуд на комплексной плоскости. Только теперь надо рассматривать не сложение амплитуд от разных штрихов, а сложение амплитуд от тонких полосок внутри одного штриха.
Часть полосок "закрыта" непрозрачной частью штриха решетки шириной b. Свет приходит только от прозрачной части штриха шириной a. Поэтому вместо двух окружностей на комплексной плоскости останется дуга, которая составляет часть окружности величины 2a/(a+b). Для m–го главного максимума (m–й порядок дифракции) на комплексной плоскости картина сложения амплитуд от одного штриха решетки даст долю окружности величины ma/(a+b). Если эта доля равна целому числу (окружностей), то амплитуда соответствующего главного максимума равна нулю.
Зоны Френеля
Определить понятие зоны Френеля можно для дифракции на отверстии любой формы и даже вообще без отверстия, но практически полезно рассмотрение зон Френеля только при дифракции на круглом отверстии, причем в случае, когда источник света и точка наблюдения находятся на прямой, перпендикулярной к плоскости экрана с отверстием и проходящей через центр отверстия.
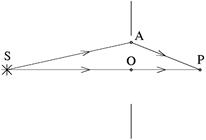
| Рис. 35 |
Именно такой случай изображен на рис. 35. Здесь S — точечный источник света, P — точка наблюдения. На зоны Френеля можно мысленно разбить любую поверхность, через которую проходит свет, например поверхность равной фазы. Но в нашем случае удобнее разбить на зоны Френеля плоскую поверхность отверстия.
Задача имеет ось симметрии, поэтому зоны Френеля имеют вид колец. Задача сводится к определению радиуса зоны Френеля с произвольным номером m. Под радиусом зоны Френеля подразумевают больший радиус кольца.
Сделаем дополнительное построение (см. рис. 35). Соединим произвольную точку A в плоскости отверстия отрезками прямых линий с источником света S и с точкой наблюдения P. Световая волна, которая приходит в точку наблюдения по пути SAP, проходит больший путь, чем волна, прошедшая по пути SOP. Разность хода SA+AP-SO-OP определяет разность фаз волн, пришедших от вторичных источников A и O в точку наблюдения P. От разности фаз зависит результат интерференции волн в точке P и, следовательно, интенсивность света в этой точке.
Если разность хода равна l/2 , то свет приходит в точку наблюдения в противофазе. Следовательно, при разности хода меньше l/2 свет приходит более или менее в одинаковой фазе.
Это условие SA+AP-SO-OP £ l/2 по определению является условием того, что точка A находится в первой зоне Френеля. Тогда для границы первой зоны разность хода SA+AP-SO-OP = = l/2.
Это равенство позволяет найти радиус первой зоны, будем обозначать его r1. Он равен длине отрезка OA при разности хода l/2.
Если оба расстояния SO и OP гораздо больше диаметра отверстия, а обычно рассматривают именно такой случай, то из геометрических соображений (см. рис. 35) можно получить
r1 =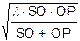 
.
Аналогично, условие для внешней границы зоны Френеля с номером m: SA+AP-SO-OP = ml/2. Отсюда радиус m–й зоны Френеля
rm =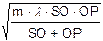 
= 
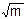×r1.
Отметим, что разбиение на зоны Френеля — это разбиение вторичного источника света на источники с одинаковой площадью, так как
Sm = p×rm2 - p×rm-12 = p×r12 = S1.
От соседних зон Френеля свет приходит в противоположных фазах, так как разность хода от соседних зон по определению равна l/2. Этот результат можно обобщить. Разбиение отверстия на такие кольца, что свет от соседних колец приходит в точку наблюдения с фиксированной разностью фаз, означает разбиение на кольца одинаковой площади. Можно доказать это в качестве задачи.
Рассмотрим теперь разбиение площади отверстия на гораздо более тонкие кольца равной площади. Эти кольца — вторичные источники света. Амплитуда света, пришедшего от каждого кольца в точку наблюдения P примерно одинакова. Разность фаз света от соседних колец в точке P тоже одинакова. Тогда комплексные амплитуды в точке наблюдения при сложении на комплексной плоскости образуют дугу окружности. Суммарная амплитуда — хорда.
Картина построения на комплексной плоскости совершенно аналогична картине для дифракции Фраунгофера на одной щели.
Рассмотрим теперь, как изменяется картина сложения комплексных амплитуд при изменении радиуса отверстия и сохранении остальных параметров задачи.
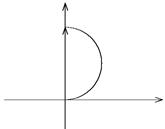
Если отверстие открывает для точки наблюдения одну зону Френеля, то картина сложения амплитуд выглядит так, как изображено на рис. 36. Амплитуда от последнего тонкого кольца повернута на угол p относительно амплитуды от центральной части отверстия, так как соответствующая разность хода по определению первой зоны Френеля равна l/2. Этот угол p означает, что амплитуды образуют половину окружности.
Если отверстие открывает две зоны Френеля, то картина сложения амплитуд будет иметь вид окружности. В этом случае суммарная амплитуда света в точке P равна нулю (нулевая длина хорды).
| Рис. 36 |
Если открыты три зоны Френеля, то картина представляет собой полторы окружности, и так далее.
Для четного числа зон Френеля амплитуда в точке наблюдения равна нулю. Для нечетного числа амплитуда одинаковая, максимальная и равна длине диаметра окружности на комплексной плоскости сложения амплитуд.
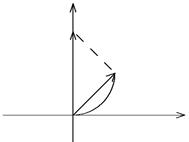
Иногда в условии задачи говорится, что открыто какое–либо дробное число зон Френеля. При этом под половиной зоны Френеля понимают четверть окружности картины сложения амплитуд, что соответствует половине площади (а не радиуса) первой зоны Френеля. Аналогично для любого другого дробного числа зон Френеля. Для половины зоны Френеля, как видно из рис. 37, амплитуда поля в корень из двух раз меньше, чем для одной зоны Френеля.
Иногда в задачах говорится, что какое–то (дробное) число зон закрыто, затем сколько–то зон открыто и остальные закрыты. Тогда суммарную амплитуду поля можно найти как векторную разность амплитуд двух задач.
| Рис. 37 Рис. 38 |
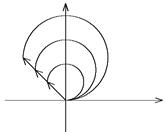
Если открыты все зоны Френеля (нет препятствия на пути световой волны), то картина сложения амплитуд будет выглядеть как спираль, что очень грубо изображено на рис. 38. Спираль получается, потому что при большом числе открытых зон следует учитывать зависимость амплитуды света, излученного вторичным источником от расстояния до точки наблюдения и от направления излучения вторичного источника. В результате свет от зон с большим номером будет иметь малую амплитуду.
Центр спирали находится в середине окружности из первых двух зон, поэтому амплитуда поля при всех открытых зонах вдвое меньше амплитуды поля при открытой одной первой зоне, а интенсивности различаются в четыре раза. Интенсивность света при открытой первой зоне Френеля в четыре раза больше интенсивности света перед экраном с отверстием.
В задачах на зоны Френеля обычно задана интенсивность света до экрана, в котором какие–то зоны Френеля открыты, какие–то — закрыты, и требуется найти интенсивность в точке наблюдения. Интенсивность — это квадрат амплитуды (с коэффициентом c/8p). И заданная интенсивность света до экрана равна квадрату радиуса окружности на комплексной плоскости. Так, если требуется найти отношение интенсивности света при открытой первой зоне к интенсивности падающей волны, то это отношение равно квадрату отношения диаметра окружности к ее радиусу.
В некоторых задачах рассматривается дифракция на небольшом непрозрачном экране, который закрывает для точки наблюдения небольшое число зон Френеля. Полезно сравнить эту задачу с дополнительной, в которой эти зоны наоборот открыты, а все остальные — закрыты. Амплитуду поля в первой задаче можно найти, как векторную разность амплитуды исходной волны и амплитуды во второй задаче.
Дифракция Фраунгофера
Дифракция Фраунгофера — это дифракция на отверстии, которое для точки наблюдения открывает заметно меньше одной зоны Френеля. Это условие выполнено, если точка наблюдения и источник света находятся достаточно далеко от отверстия.
Дифракция Френеля
Дифракция Френеля — это дифракция в случае, когда отверстие открывает (или препятствие закрывает) для точки наблюдения несколько зон Френеля. Если открыто много зон Френеля, то дифракцией можно пренебречь, и мы оказываемся в приближении геометрической оптики.
Дата: 2019-12-10, просмотров: 406.
