Тонкая линза — линза, толщина которой много меньше ее фокусного расстояния. Если линзу нельзя считать тонкой, то каждую из двух сферических поверхностей линзы можно рассматривать как отдельную тонкую линзу.
Тогда изображение в толстой линзе можно найти как изображение изображения. Первая сферическая поверхность толстой линзы дает изображение источника как изображение в тонкой линзе. Вторая сферическая поверхность дает изображение этого изображения.
Другой подход при построении изображений состоит в том, что вводится понятие главных плоскостей центрированной оптической системы, частным случаем которой может быть толстая линза. Центрированная оптическая система, которая может состоять и из большого числа линз, полностью характеризуется двумя фокальными и двумя главными плоскостями. Полностью характеризуется в том смысле, что знание положения этих четырех плоскостей достаточно для построения изображений. Все четыре плоскости перпендикулярны оптической оси, следовательно свойства оптической системы полностью определяются четырьмя точками пересечения четырех плоскостей с оптической осью. Эти точки называются кардинальными точками системы.
Для тонкой линзы обе главные плоскости совпадают с положением самой линзы. Для более сложных оптических систем существуют формулы расчета положения кардинальных точек через радиусы кривизны поверхностей линз и показатели их преломления [2].
Для построения изображения точечного источника достаточно рассмотреть прохождение через оптическую систему двух удобных нам лучей и найти точку их пересечения после линзы, либо точку пересечения продолжений лучей назад (для мнимого изображения).
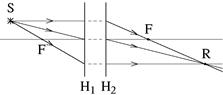
Построение хода лучей проводится так, как будто между главными плоскостями системы находится тонкая линза, а пространство между главными плоскостями отсутствует. Пример построения приведен на рис. 10. H1 и H2 — главные плоскости системы.
| Рис. 10 |
Задача прохождения света через центрированную оптическую систему может быть решена не только геометрическим построением хода лучей, но и аналитически. Для аналитического решения задач удобен матричный метод [2].
Формулы тонкой линзы
Если в задаче требуется аналитический результат, а не построение изображения, то для решения обычно достаточно трех формул:
F =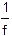 
; = 
+ 
;
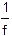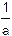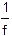= (n-1)×( 
+ 
).
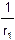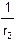Здесь F — оптическая сила линзы, f — фокусное расстояние, a — расстояние от линзы до источника света, b — расстояние от линзы до изображения, r1 и r2 — радиусы кривизны обеих поверхностей линзы, n — показатель преломления материала линзы.
В этих формулах все величины с размерностью длины могут принимать как положительные, так и отрицательные значения. Фокусное расстояние f положительно для собирающей линзы, b положительно для действительного изображения, r1 и r2 положительны для двояковыпуклой линзы. Расстояние от линзы до источника — положительная величина, но и тут можно представить себе мнимый точечный источник, для которого это расстояние будет отрицательным.
Реже встречаются задачи, в которых показатели преломления среды с двух сторон от линзы различаются. Тогда потребуются следующие формулы:
F =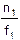 
= 
= 
+ 
.
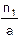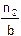Может быть полезна и формула для оптической силы одной сферической поверхности, в частности при рассмотрении толстой линзы как двух сферических поверхностей:
F =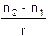 
.
Сферическое зеркало
Чтобы удовлетворить приближению параксиальной оптики, нужно потребовать, чтобы сферическое зеркало было малой частью сферы. Другими словами, размер зеркала должен быть много меньше радиуса кривизны сферы.
Сферическое зеркало отражает световые лучи аналогично оптической системе, состоящей из тонкой линзы и вплотную поставленного плоского зеркала. Вогнутое зеркало аналогично собирающей линзе, выпуклое — рассеивающей.
Модуль фокусного расстояния сферического зеркала равен половине радиуса кривизны сферы:
f =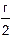 
.
Фокус расположен посередине между зеркалом и центром сферы.
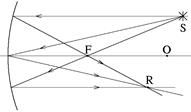
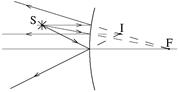
| а б Рис. 11 |
| |
На рис. 11,а,б приведены примеры построения изображений точечного источника света в сферическом зеркале.
Глаз
Часто в задачах говорится, что что–либо рассматривается глазом. При этом хрусталик глаза можно считать тонкой линзой. Эта линза дает изображение рассматриваемого предмета на задней стенке глазного яблока, где расположена сетчатка светочувствительных клеток. В задачах сетчатку глаза можно считать плоским экраном. Глаз видит изображение сфокусированным (резким), если изображение предмета в линзе хрусталика попадает в плоскость сетчатки.
Следовательно при решении задач можно считать, что глаз состоит из тонкой линзы и плоского экрана.
Фотоаппарат
Фотоаппарат полностью аналогичен глазу. Фотоаппарат — это тонкая линза и плоский экран в виде фотопластины. Чтобы изображение на фотопластине не было размытым, необходимо чтобы изображение предмета попало в плоскость фотопластины.
Окуляр
Окуляр — это линза, которую ставят перед глазом, чтобы рассмотреть близко расположенный предмет. Окуляр усиливает собирающую линзу хрусталика.
Хрусталик глаза — линза, фокусное расстояние которой может изменяться усилием глазных мышц. Фокусное расстояние f нужно изменять, чтобы рассматривать удаленные на разное расстояние предметы. По формуле тонкой линзы имеем:
= + 
,
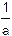где n — показатель преломления среды внутри глазного яблока, b — фиксированное расстояние от линзы хрусталика глаза до изображения (сетчатки). Чтобы отчетливо видеть предметы на разных расстояниях, нужно для каждого расстояния 'a' подбирать значение фокусного расстояния f. Глаз не может изменять фокусное расстояние в любых пределах, поэтому глаз не может настраиваться (аккомодироваться) на предметы, расположенные слишком близко. Рассмотреть близко расположенный предмет позволяет окуляр — линза, которую ставят вплотную к глазу. При этом хрусталик глаза вместе с окуляром образуют более короткофокусную линзу, чем один хрусталик. Меньшие значения f соответствуют меньшим значениям a, расстояния до предмета.
Глазные мышцы слабо изменяют параметры системы хрусталик окуляр. Поэтому для получения резкого изображения на сетчатке глаза нужно подобрать расстояние между предметом и окуляром, оставляя глаз вплотную с окуляром.
Подзорная труба, телескоп
Телескоп, или подзорная труба, — это прибор, помогающий рассмотреть удаленный предмет. Грубо говоря, телескоп — это одна линза и экран в фокусе линзы. Эту линзу называют объективом. Изображение очень удаленных предметов должно быть близко к фокальной плоскости согласно формуле: 1/f = 1/a + 1/b. Если экран поместить в фокальной плоскости, то изображение удаленных предметов будет резким, не размытым.
За изображением световые лучи идут так, как если бы они исходили от источника, расположенного в месте изображения. Поэтому можно не ставить экран в плоскости изображения, а рассматривать изображение, как предмет, висящий в этой плоскости. Единственное ограничение — нужно ставить глаз по ходу лучей так, чтобы лучи попали в глаз, т.е. нельзя изображение без экрана рассматривать сбоку.
Если вместо регистрации на фотопластине рассматривать изображение глазом, то удобно рассматривать его через окуляр. Телескопом, или подзорной трубой, называют обычно пару линз объектив–окуляр. Если вместо объектива используется сферическое зеркало, то это — зеркальный телескоп.
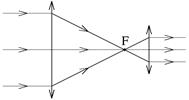
В качестве окуляра подзорной трубы может быть не только собирающая линза (труба Кеплера), но и рассеивающая (труба Галилея). Ход лучей изображен на рис. 12, 13. В обоих случаях фокусы двух линз совпадают (точка F), а увеличение подзорной трубы равно отношению фокусных расстояний линз.
| Рис. 13 |
|
Рис. 12 |
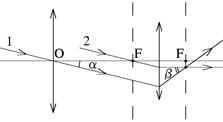
Задача определения увеличения подзорной трубы весьма поучительна, поэтому остановимся на ней чуть подробнее.
| Рис. 14 |
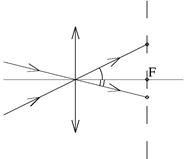
На рис. 12, 13 видно, что подзорная труба уменьшает расстояние между параллельными лучами. Однако во сколько раз подзорная труба уменьшает линейное расстояние между двумя почти параллельными лучами, во столько же раз она увеличивает угол между этими лучами. Убедиться в этом можно, например, рассмотрев ход луча 1 (рис. 14), который под некоторым углом a к оптической оси проходит через центр O объектива подзорной трубы. Если построить ход луча за окуляром (для этого полезно рассмотреть параллельный ему луч 2), то будет видно, что угол b между оптической осью и лучом возрастает в число раз, равное отношению фокусных расстояний двух линз. Обратимся теперь к рис. 15, на котором условно изображена линза хрусталика глаза. Рассмотрим два луча, проходящие через центр линзы. Будем считать, что эти лучи исходят от двух разных точек удаленного источника света. Изображения удаленных точек должны быть в фокальной плоскости линзы, на сетчатке глаза. Расстояние между двумя изображениями на сетчатке глаза пропорционально углу между лучами. Поэтому увеличение угла между лучами при прохождении лучей через подзорную трубу означает равное ему увеличение видимого глазом изображения.
Из соображений экономии места решение рассматриваемой задачи изложено не достаточно строго и подробно. Так например, лучи, проходящие через центр хрусталика глаза, изменяют направление, поскольку глазное яблоко заполнено веществом с показателем преломления заметно большим единицы, но это уточнение не влияет на вывод о равенстве увеличения угла между лучами увеличению видимого глазом изображения.
| Рис. 15 |
Дифракционный предел углового разрешения телескопа равен l/D, где D — диаметр объектива телескопа. Подробнее см. раздел "Дифракционный предел разрешения".
Микроскоп
Микроскоп — это прибор, который позволяет рассматривать увеличенное изображение близко расположенного предмета.
Грубо говоря, микроскоп, как и телескоп, — это одна линза (объектив) и экран. Но если в телескопе экран ставится в фокальной плоскости линзы, чтобы получить на нем изображение удаленного предмета, то в микроскопе рассматриваемый предмет ставится близко к фокусу линзы, чтобы получить увеличенное изображение предмета. Чем ближе предмет к фокальной плоскости, тем больше увеличение изображения предмета.
Изображение можно регистрировать на фотопластине либо рассматривать через окуляр, как и в случае телескопа. Микроскопом, как и телескопом, обычно называется пара линз объектив–окуляр.
Разрешающая способность микроскопа: lmin = l/(n×sin u), где u — угол между двумя лучами, исходящими из центральной точки рассматриваемого объекта. Один луч проходит через центр объектива, другой — направлен в край объектива. Подробнее смотри раздел "Дифракционный предел разрешения".
Шкала, крест, острие
Заглянув в окуляр оптического прибора, часто можно увидеть шкалу, крестик, острие или какие–либо другие реперы, удобные для анализа изображения. Если плоскость изображения предмета не совпадает с положением репера, то смещение глаза, перпендикулярное оптической оси, приводит к кажущемуся смещению изображения относительно репера. Такой эффект обесценивает результаты измерений с использованием репера. Чтобы устранить рассматриваемый источник ошибок, репер с помощью предусмотренных регулировок нужно поместить в плоскость изображения предмета.
Подбирая положение репера, линзу окуляра перемещают вместе с репером, а положение линзы относительно репера выбирают заблаговременно таким, чтобы глазом через окуляр можно было рассматривать репер без напряжения глазных мышц.
Чтобы репер было лучше видно, он обычно подсвечивается маленькой лампочкой, расположенной вблизи линзы окуляра.
Спектрометр
Спектрометр — прибор, позволяющий измерять распределение энергии источника света по частотам излучения.
Для решения задач по оптике редко требуется понимание работы спектрометра. Изложение здесь этого вопроса преследует цель дать представление о юстировке (настройке) оптической схемы при выполнении лабораторных работ, о том, что следует "крутить" и чего при этом добиваться. При юстировке других оптических схем используются во многом похожие принципы.
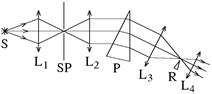
Типичная оптическая схема спектрометра изображена на рис. 16. Здесь S — источник света, L1 — конденсорная линза, SP — входная щель спектрометра, L2 — коллиматорная линза, P — призма, L3 объектив, R — репер, L4 — окуляр.
|
Рис. 16 |
Коротко обсудим назначение элементов оптической схемы и выбор положения каждого элемента схемы.
Конденсорная линза L1 собирает свет на входную щель спектрометра SP. Ее положение выбирается так, чтобы изображение источника света S в этой линзе находилось в плоскости входной щели SP. Этого можно добиться при различных положениях источника света S. Положение источника света S, в свою очередь, выбирается так, чтобы лучи, проходящие через края конденсорной линзы L1, после входной щели SP попадали на края коллиматорной линзы L2. Конструкция спектрометра должна позволять это проконтролировать. Заполнение светом всей коллиматорной линзы L2 уменьшает дифракционное уширение спектральных линий. За края коллиматорной линзы L2 свет не должен попадать, чтобы избежать ложных сигналов от паразитных отражений (бликов).
Ширина входной щели спектрометра, с одной стороны, не должна быть слишком мала, так как в этом случае спектрометр пропускает мало света и его трудно регистрировать. С другой стороны, с увеличением ширины щели падает спектральное разрешение прибора. Ширину щели выбирают следующим образом. Широкую щель сужают до тех пор пока сужение щели приводит к сужению изображения монохроматических спектральных линий на выходе спектрометра. Начиная с некоторой ширины щели, которую называют нормальной шириной, ширина изображения спектральных линий перестает уменьшаться, так как определяется дифракцией на линзах L2, L3 и призме P, а не шириной входной щели.
Коллиматорная линза L2 формирует параллельный пучок лучей, чтобы все лучи имели одинаковый угол падения на призму P. Одинаковость углов падения лучей света важна потому, что угол поворота луча призмой P зависит не только от частоты света, но и от угла падения. Неодинаковость углов падения приводит к уширению изображений монохроматических спектральных линий и к падению спектрального разрешения. Чтобы коллиматорная линза L2 создавала параллельный пучок лучей, нужно, чтобы входная щель спектрометра (SP) находилась в фокальной плоскости линзы L2. Этого добиваются, подбирая положение коллиматорной линзы L2 вдоль оптической оси, при котором ширина изображений спектральных линий минимальна.
Положение призмы P не критично. Она просто должна попасть в пучок световых лучей. Обычно угол падения на переднюю грань призмы делают близким к углу выхода света через заднюю грань.
Показатель преломления призмы зависит от частоты света, поэтому после призмы P свет каждой частоты идет параллельным пучком лучей в своем направлении. В фокальной плоскости объектива L3 формируются цветные изображения входной щели спектрометра. Каждая монохроматическая спектральная линия источника света дает свое изображение. Это и есть регистрируемый спектр.
Наблюдать изображения спектральных линий удобно через окуляр L4. Положение окуляра L4 относительно репера R выбирается так, чтобы глаз без напряжения видел репер. Положение репера вместе с окуляром вдоль оптической оси выбирается первоначально (грубо) так, чтобы видеть резкие очертания спектральных линий. Окончательно (точно) положение окуляра с репером выбирается так, чтобы плоскость изображения спектральных линий совпадала с плоскостью репера. При этом перемещение глаза перпендикулярно оптической оси не приводит к видимому смещению репера относительно спектральных линий.
Если перемещать окуляр L4 вместе с репером R поперек луча, то можно переходить от наблюдения одной спектральной линии к наблюдению другой.
Поворачивать призму P конструктивно проще, чем перемещать окуляр L4 поперек луча. Поворот призмы P приводит к перемещению цветных изображений спектральных линий относительно репера. Острие или крест (репер), которые видны через окуляр L4 , позволяют сопоставить каждой спектральной линии показания барабана, поворачивающего призму P.
ФОТОМЕТРИЯ
Фотометрия рассматривает вопросы объективной регистрации восприятия света человеком. С этой целью вводятся понятия освещенности E, светимости R, яркости B, силы света I и относительной спектральной чувствительности глаза V.
Освещенность — это поток энергии света (энергия в единицу времени), падающей на единицу площади поверхности:
E =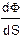 
.
Интересно сравнить освещенность с интенсивностью света, которая по определению равна потоку энергии через единицу площади. В определении интенсивности подразумевается , что площадка перпендикулярна направлению распространения света, и свет, соответственно, распространяется более или менее в одном направлении. Для света одного направления освещенность равна произведению интенсивности на косинус угла падения. При скользящем падении света освещенность мала. Освещенность имеет смысл и для произвольного распределения света по направлениям.
Светимость — то же, что и освещенность, только свет не падает на поверхность, а излучается поверхностью. Светимость — поток энергии излучения света поверхностью единичной площади.
Сила света — это поток энергии излучения света в единичный телесный угол,
I = 
.
Сила света так же, как и светимость, — характеристика источника света. Эта характеристика становится наглядной, когда источник света рассматривается издалека, и его можно считать точечным. Для удаленного источника сила света не зависит от расстояния. Освещенность E, создаваемая точечным источником силой света I, равна выражению:
E =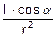 
,
где a — угол падения света, r — расстояние от источника до освещаемой поверхности.
Яркость источника света — это поток энергии света, излучаемого единицей поверхности источника в единичный телесный угол, деленный на косинус угла между нормалью к поверхности и рассматриваемым направлением излучения,
B =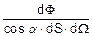 
.
Деление на косинус угла удобно потому, что яркость излучения нагретого тела почти не зависит от направления излучения. Это закон Ламберта, он идеально выполняется для излучения абсолютно черного тела. Если в условии задачи говорится о ламбертовском источнике света, то подразумевается, что яркость не зависит от направления излучения.
Для ламбертовского источника света светимость R и яркость B связаны соотношением
R = p×B.
Здесь p появляется как половина телесного угла, в который излучает поверхность. Одна вторая — это среднее по телесным углам излучения значение косинуса между нормалью к поверхности и направлением излучения.
Относительная спектральная чувствительность глаза — табулированная функция длины волны излучения. Ее максимальное значение принято за единицу.
Основные понятия волновой оптики
В монохроматической световой волне электрическое поле E и магнитное поле H изменяются с постоянной частотой w (циклическая частота), каждая проекция векторов E и H пропорциональна величине cos(wt+j). Здесь t — время, (wt+j) — фаза колебаний, j — начальная фаза, зависящая от пространственных координат. Разные проекции векторов E и H могут иметь различающиеся начальные фазы.
Поверхность с определенным значением фазы (поверхность равных фаз) перемещается в направлении волнового вектора k по нормали к поверхности со скоростью c/n (фазовая скорость света), где c — скорость света в вакууме, n — показатель преломления среды. Длина волнового вектора k называется волновым числом и по определению равна k = 2p/l = nw/c, здесь l — длина волны света.
В бегущей монохроматической световой волне векторы E и H в каждый момент времени перпендикулярны друг другу и равны по величине (в системе единиц СГС Гаусса). Направление движения световой волны перпендикулярно обоим векторам E и H, т.е. световая волна — поперечная волна. Если векторы E и H в какой–то точке пространства в какой–то момент времени не перпендикулярны друг другу или не равны по длине, то через эту точку проходит не одна, а несколько волн в различных направлениях.
Далее будем обсуждать только направление распространения световой волны S и направление вектора E, так как направление вектора H однозначно ими определяется.
Пусть световая волна распространяется в направлении оси Z. Тогда вектор E лежит в плоскости XY, поскольку E перпендикулярен направлению распространения. Если вектор E колеблется вдоль какой–то линии в этой плоскости, то световая волна называется линейно поляризованной. Если вектор E произвольно меняется в плоскости XY, то в каждый момент времени его можно разложить на сумму двух векторов вдоль осей X и Y. Произвольную волну, распространяющуюся вдоль оси Z, можно представить как сумму двух линейно поляризованных волн с колебанием вектора E вдоль осей X и Y соответственно.
Если конец вектора E вращается по окружности в плоскости XY, то такой свет называется циркулярно поляризованным, или светом с круговой поляризацией. Свет поляризован по левому кругу, если в фиксированной точке при наблюдении навстречу свету вектор E (как и вектор H) вращается по левому кругу, т.е. против часовой стрелки. Если конец вектора E описывает эллипс, то волна называется эллиптически поляризованной. Если волна монохроматическая, то конец вектора E описывает эллипс, окружность, либо вектор E гармонически колеблется вдоль линии.
Интенсивностью световой волны I называют среднее значение модуля вектора Пойнтинга. Время усреднения либо считают равным времени регистрации света, либо равным постоянной времени приемника света. Поскольку для бегущей волны векторы E и H перпендикулярны, модуль вектора Пойнтинга можно найти по формуле |S| = (c/4p)×E×H. Если еще учесть, что E = H, то получим выражение |S| = (c/4p)×E2. Следовательно, для интенсивности можно записать I = (c/4p)×<E2>, где скобки < > означают среднее по времени значение. Эта формула приближенно верна и при сложении почти однонаправленных световых волн.
При сложении двух или нескольких световых волн складываются не интенсивности волн, а напряженности E и H световых полей. Если при этом интенсивность суммы полей отличается от суммы интенсивностей, то говорят, что эти световые поля интерферируют. Если световые поля способны интерферировать, то их называют когерентными друг другу.
Если на пути распространения световой волны встречается препятствие, то волна его огибает, поворачивает "за угол". Это явление называется дифракцией. Препятствием, например, может быть любой объект, который не пропускает, "загораживает", часть фронта световой волны.
ИНТЕРФЕРЕНЦИЯ
Явление интерференции состоит в том, что при сложении двух или нескольких световых волн, суммарная интенсивность света отличается от суммы интенсивностей. Это возможно потому, что складываются напряженности E и H световых волн, а интенсивность суммы световых волн можно найти в соответствии с определением интенсивности по формуле I = (c/4p)×<E2> (в системе единиц СГС Гаусса). Здесь скобки < > означают среднее по времени значение.
Интерференцию света обычно рассматривают не в одной точке, а на плоском экране. Поэтому говорят об интерференционной картине, под которой понимают чередующиеся полосы относительно большей и меньшей интенсивности света. Основными характеристиками интерференционной картины являются ширина полос интерференции и видность интерференционной картины.
Ширина интерференционных полос — это расстояние на экране между двумя соседними светлыми или двумя темными полосами.
Видность интерференционной картины по определению равна
V =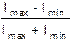 
.
Здесь Imax — интенсивность света в середине светлой полосы, Imin — в середине ближайшей темной полосы. Более строго можно ввести понятие видности, используя понятие модуля комплексной степени когерентности [2, 3].
Видность интерференционной картины меняется в пределах от 0 до 1. Нулевая видность соответствует условию Imax =Imin , при котором полосы просто отсутствуют (равномерно освещенная область экрана). Видность, равная единице, соответствует условию Imin = 0.
Волны с ортогональными линейными поляризациями не интерферируют, так как для них интенсивность суммарной волны всегда равна сумме интенсивностей исходных волн. В том же смысле ортогональны лево и право циркулярно поляризованные волны.
Наиболее часто обсуждаемые в задачах по оптике поляризационные устройства — поляризатор и фазовые пластинки l/2 и l/4.
Поляризатор
Идеальный поляризатор — это оптическое устройство, которое полностью пропускает одну линейную поляризацию и полностью поглощает поляризацию, ортогональную к ней. Свет, распространяющийся в фиксированном направлении, всегда можно мысленно представить как сумму двух линейно поляризованных во взаимно перпендикулярных направлениях волн, каждая из которых распространяется в том же направлении. Поляризатор оставляет одну из этих волн.
Пластинки l/2 и l/4
Плоскопараллельную фазовую пластинку l/2 или l/4 изготавливают из одноосного кристалла, так что направление оси кристалла лежит в плоскости пластинки. Свет, падающий перпендикулярно на фазовую пластинку, распространяется в ней в виде двух независимых световых волн, линейно поляризованных во взаимно перпендикулярных направлениях. Поляризация (направление вектора E) обыкновенной волны перпендикулярна оси кристалла. Поляризация необыкновенной волны совпадает с направлением оси кристалла.
Для каждой из двух волн кристалл имеет свой показатель преломления n1 и n2 . От показателя преломления зависит оптическая толщина пластинки n×h, где h — геометрическая толщина. Поэтому две волны на выходе из кристалла приобретают оптическую разность хода (n1-n2)×h. Если разность хода равна l/2, то фазовая пластинка называется пластинкой l/2. Если l/4, то — l/4. Подробнее понятие оптической разности хода обсуждается в одном из следующих разделов.
Эта разность хода изменяет разность фаз двух линейно поляризованных волн на величину (2p/l)×(n1-n2)×h.
Пластинка l/4 интересна тем, что она позволяет получить циркулярно поляризованный свет из линейно поляризованного и наоборот. Чтобы получить циркулярно поляризованный свет из линейно поляризованного, направление линейной поляризации на входе пластинки l/4 должно составлять угол p/4 с направлением оси кристалла (свет падает перпендикулярно пластинке). Только в этом случае амплитуды обыкновенной и необыкновенной волн в кристалле равны.
На входе в кристалл эти две волны синфазные в случае линейной поляризации падающей волны. Тогда разности хода l/4 на выходе пластинки соответствует разность фаз p/2. За пластинкой при сложении двух линейно поляризованных волн с одинаковой амплитудой, взаимно ортогональной поляризацией и разностью фаз p/2 образуется циркулярно поляризованная волна.
Двухлучевая интерференция
Под двухлучевой интерференцией понимают интерференционную картину, возникающую при сложении двух световых волн одинаковой частоты.
Рассмотрим простейшую задачу по интерференции. Пусть две линейно поляризованные в одном направлении световые волны приходят в одну точку экрана и имеют в этой точке зависимость напряженности электрического поля от времени в виде E1=E0×cos(wt+j1) и E2=E0×cos(wt+j2). Выразим интенсивность суммарной световой волны I через одинаковую интенсивность падающих световых волн, которую обозначим I0:
I0 =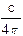 
ž<E12> = 
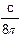žE02:
I = 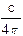ž<E2> = 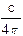ž<(E0×cos(wt+j1)+E0×cos(wt+j2))2> =
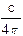= žE02ž<cos2(wt+j1)+2×cos(wt+j1)×cos(wt+j2)+cos2(wt+j2)> =
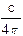= žE02ž( 
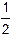+ <2×cos(wt+j1)×cos(wt+j2)> + ) =
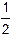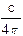= žE02ž( 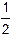+ <cos(2wt+j1+j2)> + cos(j1-j2) + ) =
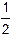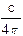= žE02ž(1+cos(j1-j2)) =
= 2×I0×(1+cos(j1-j2)).
В этой задаче сумма интенсивностей падающих волн равна 2I0. Интенсивность суммарной волны I бывает как больше, так и меньше суммы интенсивностей в зависимости от разности фаз интерферирующих волн. Светлая полоса (большая интенсивность) соответствует нулевой разности фаз, темная — разности фаз, равной p.
При сложении двух волн одинаковой поляризации с интенсивностями I1 и I2 интенсивность суммарной волны получаем аналогично:
I = I1+I2+2× 
×cos(j1-j2).
Оптическая разность хода
Вместо разности фаз dj интерферирующих волн удобно ввести в рассмотрение пропорциональную ей величину D — оптическую разность хода, которая отличается множителем l/2p, где l — длина световой волны:
= 
.
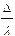Изменению разности фаз на 2p соответствует изменение разности хода на l.
В вакууме оптическая разность хода в отличие от разности фаз имеет наглядную интерпретацию. Если две интерферирующие волны испускаются одним источником света, то разность хода — это геометрическая разность длин путей, по которым два интерферирующих луча от одной точки источника достигли одной точки экрана.
| Рис. 17 |
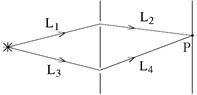
Например, в оптической схеме опыта Юнга, изображенной на рис. 17, разность хода для точки P на экране находится по формуле
D = (L1+L2)-(L3+L4).
В изотропной среде скорость света в n раз меньше, чем в вакууме, здесь n — показатель преломления среды. Частота света в среде и в вакууме одинакова, поэтому длина волны в среде в n раз меньше. В соответствии с соотношением dj/2p = D/l вместо реального уменьшения длины волны l можно рассматривать неизменную l и соответствующее увеличение длины пути луча. С этой целью вводится понятие оптической длины пути, которая в n раз больше геометрической длины. Далее, употребляя термин "разность хода", всегда будем иметь в виду оптическую разность хода.
Заменяя разность фаз интерферирующих волн оптической разностью хода, получаем следующее выражение для интенсивности интерференционной картины:
I = I1+I2+2×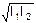 
×cos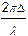 
.
Приемники света в оптическом диапазоне реагируют на интенсивность света, а не на напряженность электрического или магнитного полей. Поэтому измеряемые в опыте величины, ширина полос и видность, также могут быть выражены через интенсивность, а значит и через оптическую разность хода. Следовательно, понятие оптической разности хода позволяет свести оптическую задачу по интерференции к геометрической задаче отыскания разности хода.
Отметим, что разность хода лучей можно отсчитывать не только как разность длин путей от источника до точки наблюдения, но и как разность длин путей от двух точек любой поверхности равной фазы волны до точки наблюдения. При этом, конечно, две точки на поверхности равной фазы — не произвольные точки, а должны быть точками, через которые реально проходят лучи, попадающие в точку наблюдения. Так на рис. 17 L1=L3, поэтому две щели находятся на поверхности равной фазы, и, следовательно, разность хода можно найти по упрощенной формуле D=L2-L4. Этот прием часто используется при решении задач.
Дата: 2019-12-10, просмотров: 646.
