Принятие правильного и своевременного решения – главная задача менеджера любого уровня.
В зависимости от полноты информации используются правила принятия решений в условиях неопределенности (при отсутствии численных значений вероятностей исходов) и в условиях риска (при наличии численных значений вероятностей исходов).Все эти подходы и рассматриваются в данной теме. Кроме того, здесь же вводятся и анализируются понятия стоимости достоверной информации и полезности при определении размеров риска.
Для успешного освоения темы после изучения теоретического материала следует ответить на вопросы для самоконтроля и выполнить задание по теме 2 Практикума.
Ключевые понятия темы:
Альтернативы независимые, зависимые; критерий оценки альтернатив, лицо, принимающее решение (ЛПР), неопределенность, ожидаемая денежная оценка, оценка риска, стоимость достоверной информации, функция полезности.
2.1. Правила принятия решений в условиях неопределенности (без использования численных значений вероятностей исходов – правила максимакса, Вальда, Сэвиджа, Лапласа)
Рассмотрим правила принятия решений в условиях неопределенности на небольшом примере.
Пример 2. Пусть себестоимость пирожного в нашей кондитерской составляет 7 руб., свеженькое продаем за 13 руб., а невостребованное за день сдаем на свиноферму за 3 руб. Сколько пирожных надо производить в день, если известно лишь, что спрос на них составляет от 1 до 5?
Составим таблицу возможных доходов, расположив построчно наши альтернативы (производить от 1 до 5 пирожных), а в столбцах исходы (продать от 1 до 5), имея в ввиду, что доход от продажи одного пирожного составляет 6 руб., а потери при не продаже составляют 4 руб. (табл.3).
Доход (прибыль) в день Таблица 3
| Объем производства | Возможные исходы: спрос пирожных в день | ||||
| –2 | |||||
| –6 | |||||
| –10 |
2.1.1. Правило максимакса – максимизация максимального дохода. В каждой альтернативе найдем исход с максимальной оценкой (в табл.3 они все находятся в последнем столбце), и выбираем альтернативу, позволяющую получить самый большой доход. В нашем примере это соответствует решению производить 5 пирожных. Данный подход использует азартный карточный игрок (или пан или пропал).
2.1.2. Правило максимина (Вальда) – максимизация минимального дохода. В каждой альтернативе найдем исход с минимальной оценкой (в табл.3 они все находятся в первом столбце), и выбираем альтернативу, позволяющую максимизировать доход в самых худших для нас исходах. В нашем примере это соответствует решению производить 1 пирожное. Это очень осторожный подход к принятию решений – стратегия крайнего пессимиста.
2.1.3. Правило минимакса (Сэвиджа) – минимизация максимально возможных потерь. Составим таблицу возможных потерь или упущенной выгоды (табл.4). Она составляется из таблицы доходов следующим образом:
для каждого исхода (столбца) находится максимальный доход, затем вычисляются максимально возможные потери всех альтернатив данного исхода (из максимального дохода вычитается доход соответствующей альтернативы).
Для каждой альтернативы находятся максимально возможные потери (выделены жирным цветом). Затем выбирается та альтернатива, которой соответствует минимальное значение максимальных потерь. В данном примере этому правилу подходят альтернативы выпускать три или четыре пирожных в день.
Возможные потери в день Таблица 4
| Объем производства | Возможные исходы: спрос пирожных в день | ||||
2.1.4. Правило, основанное на принципе неопределенности Лапласа. В соответствие с этим принципом предполагается, что все исходы равновозможные, поэтому выбирается альтернатива, дающая максимальный средний доход. В нашем примере этому правилу отвечают те же альтернативы выпускать три или четыре пирожных в день, имеющие средний доход 12 (у первой альтернативы средний доход 6, у второй и пятой – 10).
2.2. Критерий Гурвица – компромиссный способ принятия решений
Этот способ принятия решения представляет собой компромисс между осторожным правилом максимина (Вальда) и оптимистичным правилом максимакса. ЛПР задает уровень пессимизма р (вероятность худшего исхода), тогда оптимистичному исходу дается вероятность 1–р, и выбирается альтернатива, дающая наибольший средневзвешенный доход при наличии только пессимистического и оптимистического исходов с заданными вероятностями.
Так, в нашем примере, худший исход – спрос на одно пирожное в день (2.1.2), лучший – пять пирожных (2.1.1). Зададим уровень пессимизма 0.4, тем самым мы предполагаем, что на каждые 4 дня худшего спроса в одно пирожное приходится 6 дней лучшего спроса в 5 пирожных. Рассчитаем средневзвешенные доходы для каждой альтернативы (табл. 5).
Критерий Гурвица Таблица 5
| Объем производства | Доход при спросе в день | Вероятность исхода | Средневзвешенный доход | ||
| 0.4 | 0.6 | ||||
| 2.4 | +3.6 | =6 | |||
| 0.8 | +7.2 | =8 | |||
| –2 | –0.8 | +10.8 | =10 | ||
| –6 | –2.4 | +14.4 | =12 | ||
| –10 | –4.0 | +18.0 | =14 |
В данном случае максимальный средневзвешенный доход имеет решение выпускать пять пирожных в день.
2.3. Правила принятия решений с использованием численных значений вероятностей исходов
Пусть теперь нам известны вероятности всех исходов.
Например, дана статистика продаж за последние 50 дней (табл. 6).
Относительные частоты (вероятности) дневного спроса на пирожные Таблица 6
| Продано пирожных в день | |||||
| Частота | |||||
| Относительная частота (вероятность) | 0.1 | 0.2 | 0.3 | 0.3 | 0.1 |
2.3.1. Правило максимальной вероятности – максимизация наиболее вероятных доходов. Наибольшая вероятность 0.3 соответствует спросу в три и четыре пирожных в день. Рассмотрим теперь доходы при каждом из этих исходов и выберем альтернативу, дающую наибольший доход (см. табл. 3). При спросе в 3 пирожных наибольший доход дает альтернатива производить 3 пирожных (доход составляет 18 руб.), при спросе в 4 пирожных наибольший доход дает альтернатива производить 4 пирожных (доход составляет 24 руб.), следовательно, по этому правилу надо производить 4 пирожных в день.
2.3.2. Оптимизация математического ожидания. Выбирается решение либо с наибольшим ожидаемым доходом, либо с наименьшими возможными потерями. Использование критерия математического ожидания наиболее приемлемо в случаях многократного принятия решения в одинаковых условиях, позволяя максимизировать среднюю прибыль (или минимизировать средние убытки) при большом временном промежутке. В соответствии с законом больших чисел (который мы проходили в разделе 3 «Математики») при многократном принятии решения мы как раз и получим математическое ожидание (среднее значение) дохода либо потерь.
а) Максимизация ожидаемого дохода.
Составим таблицу ожидаемых доходов для каждой альтернативы (табл.7).
Возможный доход (вероятность × доход из табл. 3) Таблица 7
| Объем производства | Возможные исходы: спрос пирожных в день | Ожидаемый доход | ||||
| 0.6 | 1.2 | 1.8 | 1.8 | 0.6 | ||
| 0.2 | 2.4 | 3.6 | 3.6 | 1.2 | ||
| –0.2 | 1.6 | 5.4 | 5.4 | 1.8 | ||
| –0.6 | 0.8 | 4.2 | 7.2 | 2.4 | ||
| –1.0 | 0.0 | 3.0 | 6.0 | 3.0 |
Максимальное значение ожидаемого дохода 14 руб. в день, следовательно, используя критерий максимизации ожидаемого дохода необходимо производить три или четыре пирожных в день.
б) Минимизация возможных потерь.
Составим таблицу возможных потерь для каждой альтернативы (табл.8).
Минимальные ожидаемые возможные потери равны 4.6 руб. в день, т.е. наилучшее решение – также как и в случае а, производить три или четыре пирожных в день.
Возможные потери (вероятность ∙ потери из табл. 4) Таблица 8
| Объем производства | Возможные потери: спрос пирожных в день | Ожидаемые возможные потери | ||||
| 1.2 | 3.6 | 5.4 | 2.4 | 12.6 | ||
| 0.4 | 1.8 | 3.6 | 1.8 | 7.6 | ||
| 0.8 | 0.8 | 1.8 | 1.2 | 4.6 | ||
| 1.2 | 1.6 | 1.2 | 0.6 | 4.6 | ||
| 1.6 | 2.4 | 2.4 | 1.2 | 7.6 |
Значения вероятностей из табл.6 основаны на статистической либо экспертной информации, которая подвержена изменениям. Исследование зависимости выбора решения от изменений значений вероятностей называется анализом чувствительности решения (табл. 9).
Зависимость выбора решения от изменений значений вероятностей Таблица 9
| Наименование показателей | Возможные решения: объем производства в день | ||||
| Базовые вероятности | 0.1 | 0.2 | 0.3 | 0.3 | 0.1 |
| Ожидаемый доход в день | |||||
| Альтернативные вероятности (1) | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
| Ожидаемый доход в день (1) | |||||
| Альтернативные вероятности (2) | 0.1 | 0.2 | 0.2 | 0.2 | 0.3 |
| Ожидаемый доход в день (2) |
В альтернативном варианте (1) решение, дающее максимальный доход, не претерпело изменений, хотя средняя прибыль снизилась с 14 руб. до 12 руб. В альтернативном варианте (2) решение изменилось, наибольший средний доход 15 руб. дает альтернатива производить 4 пирожных в день. Таким образом, выбор решения оказался нечувствителен к варианту (1) изменений вероятностей, но чувствителен к варианту (2).
2.4. Стоимость достоверной информации
Неопределенность при принятии решений может быть уменьшена путем сбора дополнительной информации, за которую нужно платить. Максимальная сумма денег, которую стоит заплатить, и является стоимостью достоверной информации. Так, если бы мы в нашей кондитерской заранее знали спрос на следующий день, то готовили бы столько пирожных, сколько обеспечивают максимальный доход (см. диагональ табл.3). В этом случае ожидаемый доход был бы равен
6∙0,1+12∙0,2+18∙0,3+24∙0,3+30∙0,1=18,6.
Стоимость достоверной информации есть разница между этим ожидаемым доходом и максимальным ожидаемым доходом без достоверной информации (см. 2.3.2. а). Это число 18.6 – 14 = 4.6 равно минимальным ожидаемым возможным потерям (см. 2.3.2. б). Таким образом, наша кондитерская может заплатить 4.6 руб. в день за информацию о спросе да следующий день, т.е. это максимальная плата за маркетинговые услуги.
2.5. Использование математического ожидания и среднего квадратичного отклонения для оценки риска
Если решение принимается однократно, то необходимо определить степень отклонения от математического ожидания, т.е. вычислить дисперсию и среднее квадратичное отклонение для оценки риска.
Чем меньше среднее квадратичное отклонение, тем больше уверенности, что принятое решение даст результат, близкий к математическому ожиданию.
Рассмотрим применение среднего квадратичного отклонения для оценки риска на небольшом примере.
Пример 3. Предприятие производит некоторую продукцию, спрос на которую в течение месяца 6, 7, 8 или 9 ящиков с вероятностями 0,1; 0,3; 0,5; 0,1 соответственно. Затраты на производство одного ящика равны 45 тыс. руб. Предприятие продает один ящик по цене 95 тыс. руб. Если ящик с продукцией не продается в течение месяца, то она портится и предприятие не получает дохода. Сколько ящиков следует производить?
Рассчитаем доходы по каждой альтернативе и каждому исходу, математическое ожидание дохода и среднее квадратичное отклонение по каждой альтернативе и занесем в табл. 10.
Таблица 10
| Объем производства (ящиков) | Возможные исходы: спрос ящиков в месяц | Ожидаемый доход (тыс. руб.) | Среднее квадратичное отклонение | |||
| (0,1) | (0,3) | (0,5) | (0,1) | |||
| 340,5 | 28,5 | |||||
| 352,5 | 63,73 | |||||
Поясним расчеты для альтернативы производить 8 ящиков.
Если спрос 6 ящиков, то доход составит 6∙95 – 8∙45 = 210 тыс. руб.
Если спрос 7 ящиков, то доход составит 7∙95 – 8∙45 = 305 тыс. руб.
Если спрос 8 ящиков, то доход составит 8∙95 – 8∙45 = 400 тыс. руб.
Если спрос 9 ящиков, то доход тот же, так как произведено всего 8.
Ожидаемый доход 210∙0,1+305∙0,3+400∙0,5+400∙0,1=352,5.
Дисперсия дохода составит (210 –352,5)2∙0,1 + (305–352,5)2∙0,3 +
+ (400–352,5)2∙0,5+(400–352,5)2∙0,1=4061,25.
Среднее квадратичное отклонение равно  =63,73.
=63,73.
Итак, если принимаемое решение будет многократно использовано, то лучшая альтернатива производить 8 ящиков в месяц, при этом будет обеспечен максимальный средний доход 352,5 тыс. руб. Но, если необходимо принять разовое решение, то предпочтительнее произвести 7 ящиков, при этом ожидаемая прибыль несколько меньше, зато риск резко сокращается: в первом случае ожидаемая прибыль будет лежать в пределах 352,5 ± 63,73, а во втором случае ожидаемая прибыль будет лежать в пределах 340,5 ± 28,5. В любом случае решение должен принимать руководитель с учетом его опыта, склонности к риску и степени достоверности оценок вероятностей спроса. Вся информация для принятия решения содержится в табл. 10.
2.6. Использование понятия полезности при определении размеров риска
На принятие решения оказывают большое влияние субъективные качества лица, принимающего решение (ЛПР), такие как:
· финансовое состояние ЛПР;
· отношение ЛПР к риску вообще;
· настроение или состояние здоровья ЛПР;
· множество других, даже непосредственно не относящихся к бизнесу причин.
Теория полезности позволяет ЛПР влиять на денежный результат исходов согласно своим оценкам их полезности. Каждый может приспосабливать процесс принятия решения к своим запросам.
Пример 4. Для примера рассмотрим два варианта инвестиций 1000 руб.
По первому варианту без риска можно получить 10% прибыли на вложенный капитал, по второму варианту можно, либо потерять весь капитал с вероятностью 0,6, либо его удвоить с вероятностью 0,4.
В первом случае гарантированный выигрыш составит 100 руб., во втором случае средний выигрыш равен 0∙0,6+1000∙0,4 = 400 руб.
Относительно получаемого среднего выигрыша вторая альтернатива явно предпочтительна, и если игрок безразличен к риску, он ее и выберет. Если он к риску не безразличен, а подавляющее число людей именно таковыми и являются, то выбор будет зависеть главным образом от финансового состояния игрока. Игроки, имеющие скромный денежный доход, предпочтут не рисковать, и выберут гарантированный доход в 100 руб. Для игрока, обладающего достаточно крупным капиталом, проигрыш 1000 руб. невелик, и он предпочтет рискнуть. Рисковать будут также игроки, патологически склонные к финансовым авантюрам.
Таким образом, каждый игрок по-разному оценивает полезностьтого или иного исхода. Американскими учеными Дж. Нейманом и О. Моргенштерном была предложена методика численного определения функции полезности, и было показано, что игрок при принятии решения (выбор альтернативы) будет стремиться к максимизации ожидаемой полезности, которая вычисляется как математическое ожидание полезностей всех исходов, составляющих данную альтернативу.
Процедура построения индивидуальной функции полезности U(x) состоит из двух этапов.
Этап 1. Присваиваются произвольные значения полезностей выигрышам для худшего (хmin) и лучшего (xmax) исходов (например, U(xmin)=0 и U(xmax)=100). Тогда полезности промежуточных выигрышей будут находиться в интервале от 0 до 100.
Этап 2. Игроку предлагается на выбор: получить некоторую гарантированную сумму v, находящуюся между хmin и xmax, либо принять участие в игре, в которой с вероятностью р выигрывается сумма xmax и с вероятностью (1 – р) сумма хmin. При этом вероятность р меняется до тех пор, пока игрок станет безразличным в отношении к выбору между получением гарантированной суммы v и игрой. Пусть указанное значение вероятности равно р0. Тогда
U(v)= р0U(xmax)+ (1 – р0)U(xmin).
Таким образом, строится функция полезности для любого v.
В общем случае график функции полезности может быть трех типов (рис. 1).
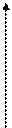
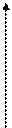
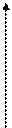 U U U
U U U
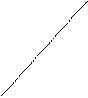 а б в
а б в
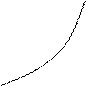

Рис. 1. Типы функций полезности Неймана – Моргенштерна для игрока, не склонного к риску (а), безразличного к риску (б), склонного к риску (в).
В рассмотренном выше примере xmin= –1000, а xmax =1000. Пусть U(xmin)=0 и U(xmax)=100. Необходимо оценить полезность гарантированного выигрыша v=100. Если игрок (средне обеспеченный) согласен принять участие в игре (выиграть 1000 с вероятностью р или проиграть 1000 с вероятностью (1 – р)) вместо гарантированного выигрыша в 100 руб. при условии, что р не менее 0.8, значит р0=0,8 и U(100)=0,8∙100+0,2∙0 =80.
Ожидаемая полезность первой альтернативы будет равна 80, а ожидаемая полезность второй альтернативы 0,6∙0+0,4∙100 = 40, то есть для данного игрока предпочтительнее первая (безрисковая) альтернатива. В данном случае это решение прямо противоположно выбору, сделанному на основе критерия ожидаемого дохода, из-за учета риска, связанного с возможным исходом инвестиций по второму варианту.
Дата: 2016-10-02, просмотров: 369.