Расчету подлежат все одиночные зубчатые передачи, а в групповых передачах - более нагруженные, т.е. передающие больший крутящий момент.

При большом перепаде передаточных отношений в группе передач с одинаковым модулем в менее нагруженных передачах (например, в ускоряющих) следует скорректировать ширину зубчатых колес в сторону уменьшения.

В соответствии с ГОСТ 21354-75 производится расчет на контактную выносливость активных поверхностей зубьев и расчет зубьев на выносливость при изгибе.

Предварительно определяется ориентировочное значение модуля по напряжениям изгиба по приведенной на рис. 6.2. номограмме или проектировочным расчетом на выносливость зубьев при изгибе по формуле:

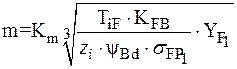(6.6)

где K_m - вспомогательный коэффициент, для прямозубых передач K_m = 14 ;

T_iF - исходная рaсчетная нагрузка (передаваемый крутящий момент), Нм (кгс · м);

K_FB - коэффициент, унитывающий распределение нагрузки по ширине венца;

Y_F1 - коэффициент, учитывающий формулу зубы;

z₁ - число зубьев шестерни;

y_Bd - вспомогательный параметр;

s_FP1 - допускаемое напряжение, МПа (кгс/мм²).

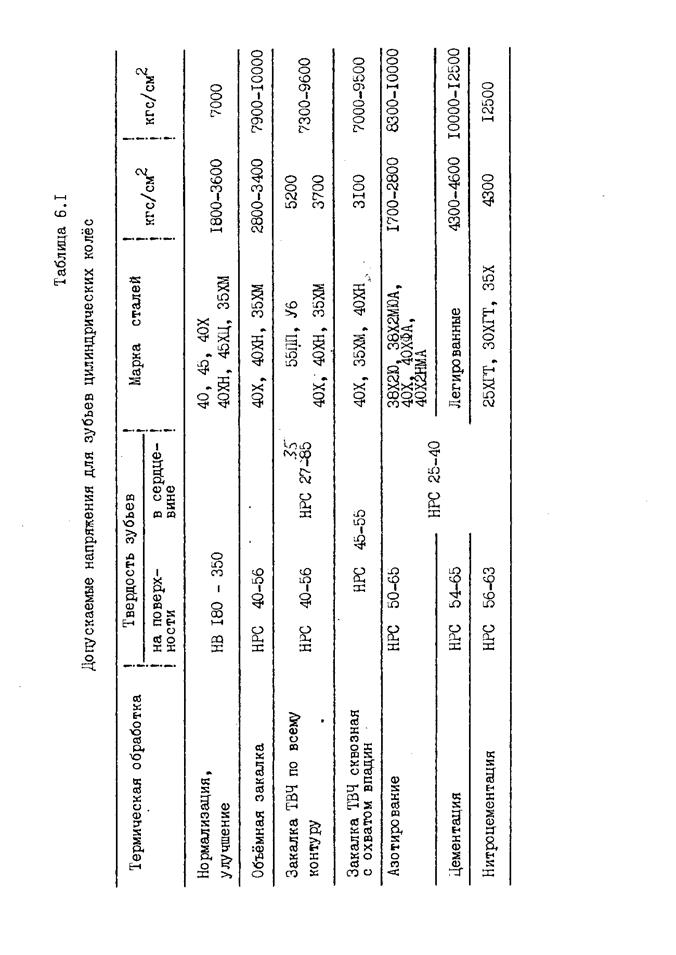
При определении модуля по формуле (6.6) необходимые для расчета данные берут из ГОСТ 21354-75. Допускаемые напряжения при предварительном расчете модуля по номограмме следует брать из табл.6.1.

Следует обравить внимание на особенность выбора расчетной нагрузки (крутящего момента) при расчете зубчатых передач и уточненном раечете валов универсальных металлорежущих станков.

При большом диапазоне регулирования R_n частоты вращения шпинделя определние крутящего момента M по минимальному числу оборотов шпинделя приведет к увеличению габаритов коробки, так как размеры шестерен и других деталей зависят от М. Поэтому для определения крутящего момента M в коробках скоростей универсальных станков в качестве расчетного числа оборотов Пр берут не минимальное число оборотов n_min , а расчетное

(6.7)

и по нему рассчитывают крутящий момент (или по ГЧВ расчетная ступень

z_p = z / 4 + 1 , (6.8)

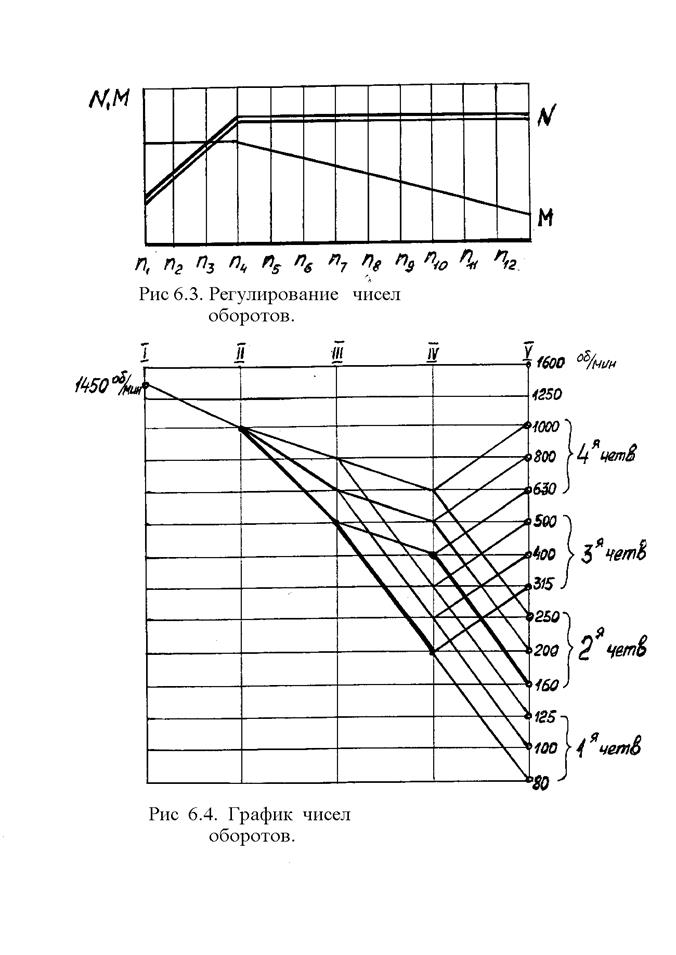
т.е. первая ступень второй четверти снизу). В этом случае на трех четвертях диапазона регулирование чисел оборотов будет осуществляться с постоянной мощностью, а на одной четверти нижних чисел оборотов - с постоянным моментом M (рис.6.3), который ограничивается не мощностью электродвигателя, а прочностью или долговечностью деталей привода. Как видно из ГЧВ (рис.6.4) расчетным числом оборотов для вала V будет не 80 об/мин, а n_p = 160 об / мин.

Расчет модуля шестерни в групповой передаче между валами IV и V следует определять при n_p = 400 об / мин.

Такое ограничение крутящего момента следует считать целесообразным еще и потому, что в средних условиях эксплуатации 80...90% машинного времени станки общего назначения работают с потреблением мощности N < 0,5 N_ном и на нижнюю четверть диапазона приходится лишь 5...10% машинного времени [6].

В пояснительной заииске приводится расчет одной групповой передачи на контактную выносливость и на выносливость зубьев при изгибе, а результаты расчета всех других передач, приводятся в виде табл.6.2.

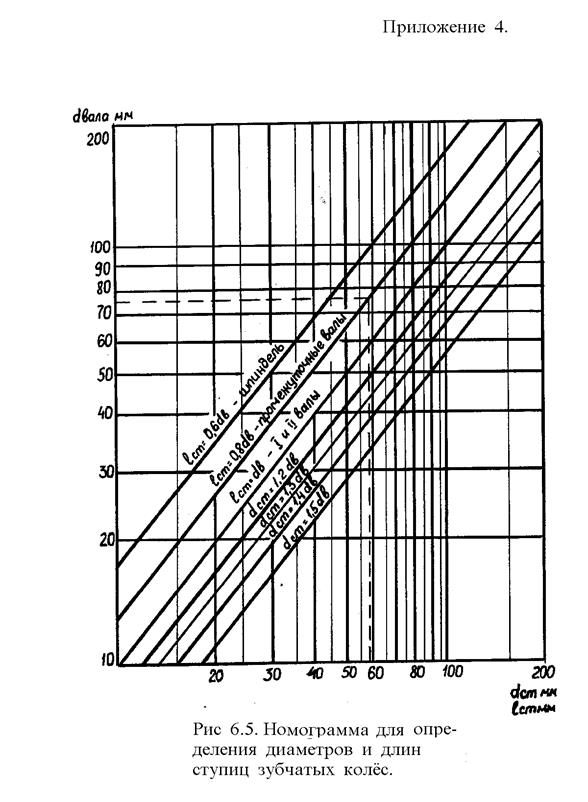
Диаметры и длины ступиц зубчатых колес в коробке скоростей можно определить по номограмме (Рис. 6.5).

Уточненный расчет валов.

Уточненный расчет валов производится после того, как завершен расчет зубчатых колес и известны все их параметры, намечены места

посадки колес, подшипников и прочих деталей на валы, т.е. когда известна компоновка развертки коробки передач. Целью такого расчета является проверка приближенно определенных диаметров валов с учетом изгибающих и крутящих моментов от всех сил, действующих на вал в различных сечениях. В записке приводится схема свертки валов привода с передачами, оказывающими наибольшее влияние на деформацию валов (Рис.6.6). Расчет валов ведется в следующем порядке:

а) рассчитываются усилия, действующие в передачах. Так, например, для цилиндрических прямозубых передач окружная и радиальная составляющие, действующей в зацеплении силы, соответственно равны

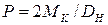(6.9)

(6.10)

где M_k - крутящий момент, кгс·см;

D_н - диаметр начальной окружности зубчатого колеса, установленного на рассчитываемом валу, см;

a - угол зацепления;

б) составляется схема нагружения вала по типу (рис.6.7). Для этого действующие силы на вал раскладываются на горизонтальные и вертикальные составляющие и по уравнениям курса сопротивления материалов, подсчитываются изгибающие момента в горизонтальной и вертикальной плоскостях;

в) строятся эпюры изгибающих моментов в обеих плоскостях;

г) определяется суммарный изгибающий момент в различных сечениях вала по формуле:

(6.11)

д) строится эпюра суммарного изгибающего момента;

е) строится эпюра наибольшего крутящего момента;

ж) определяется приведенный момент по четвертой теории прочности

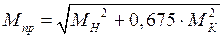(6.12)

и строится эпюра приведенного момента;

з) по анализу эпюр определяется опасное сечение вала. Составляется уравнение прочности

(6.13)

где [s] - допускаемое напряжение, кгс/см²;

W - момент сопротивления в опасном сечении, см³.

Для круглого сплошного сечения

(6.14)

Для круглого полого сечения

, (6.15)

где d - наружный диаметр вала, см;

d₀ - диаметр отверстия вала, см.

Подставив выражение (6.14) в уравнения прочности (6.13), определяют диаметр вала в опасном сечении

(6.16)

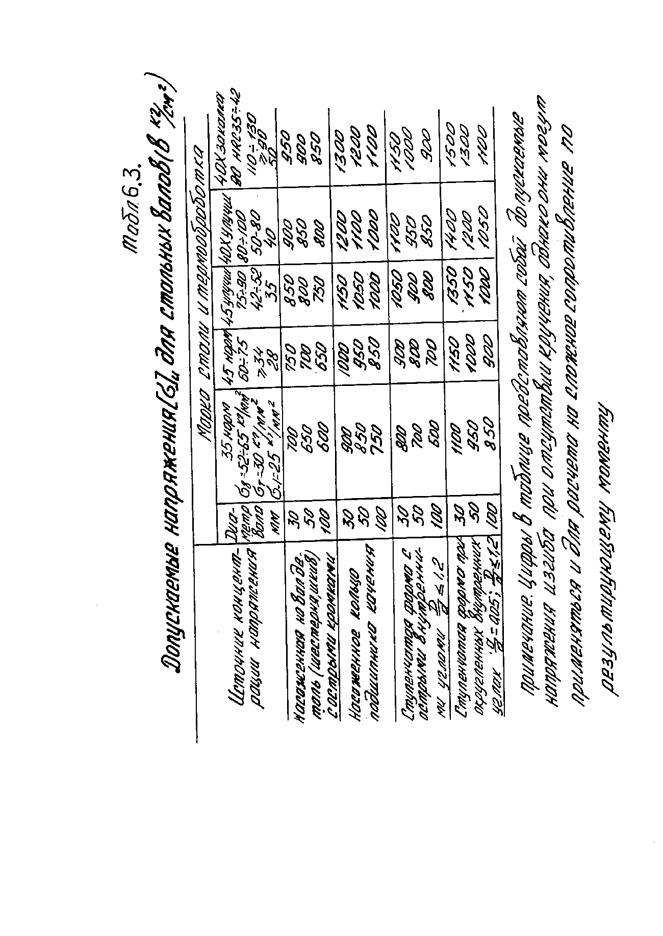Допускаемые напряжения [s_и ] берутся из табл.6.3.

Примечание. Действие сил и моментов можно рассматривать не в горизонтальной и вертикальной плоскостях, а в любых двух взаимно перпендикулярных плоскостях.

В записке приводится полный расчет одного из валов привода, а результаты расчета остальных валов сводятся в табл.6.4 с приведением в ней схем нагрузок.

Таблица 6.4