Качество изготовленной детали и эффективность работы станка зависят от принятого режима резания. Желательно устанавливать оптимальный режим: глубину резания t, подачу S и скорость главного движения резания v. Занижение режимов ведет к потере производительности, точности или экономичности невыгодно (быстрое затупление инструмента и пр.).

Требуемая скорость главного движения резания на токарном станке v(м/мин)обеспечивается настройкой частоты вращения шпинделя n (мин^-1). Они связаны следующей зависимостью:

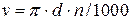или

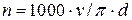
где d - диаметр обрабатываемой заготовки, мм. При заданном d и рекомендуемой скорости v по второму выражению находят n.

Регулирование скорости движения может быть бесступенчатым или ступенчатым. При бесступенчатом регулировании можно установить любую частоту вращения шпинделя в пределах, обеспечиваемых станком. Это хорошо для оптимизации режимов обработки, но не всегда возможно (пределы бесступенчатого регулирования иногда очень ограничены) и не всегда выгодно (бесступенчато регулируемые источники движения сложнее, дороже, менее надежны, чем нерегулируемые). Сочетание нерегулируемых двигателей с механическими регуляторами - вариаторами имеет те же недостатки. Поэтому, хотя бесступенчатое регулирование применяется все шире, часто ограничиваются ступенчатым регулированием. Оно обеспечивает дискретный (прерывный) ряд значений скорости.

Выражение 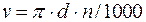при постоянном (определенном) значении n является уравнением прямой (рис. 2.2), проходящей через начало координат (если d = 0, то и v = 0). Ряд частот вращения изображается графически в виде лучевой диаграммы - пучка лучей. Она связывает параметры v, d, n и позволяет по двум из них найти третий. Например, если при d = 100 мм установить n = 355 мин^-1, то v = 112 м/мин. Полученную скорость сравнивают с рекомендуемой в справочниках. Чаще определяют n исходя из d и v.

Для построения лучевой диаграммы удобно провести вспомогательную вертикаль через точку, где d = 318,3 мм. При таком диаметре v = n.

Через точки оси ординат, где v равно n, проводят горизонтали. Каждый луч должен проходить через пересечение вспомогательной вертикали с одной из проведенных горизонталей.

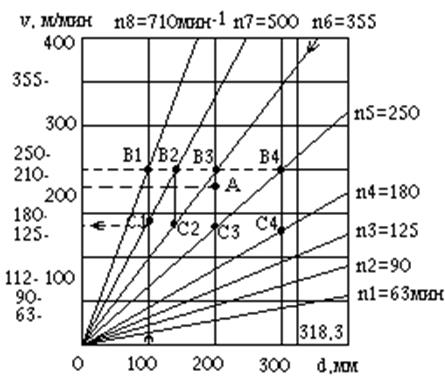
Рис 2.2. Лучевая диаграмма

При ступенчатом регулировании некоторой паре значений d и v соответствует на диаграмме расчетная точка, которая может не совпадать ни с одной из имеющихся наклонных прямых. Так, при d = 200 мм и v = 210 м·мин. получается точка А между n₅ и n₆. Диаграмма отражает только те частоты вращения, которые фактически можно установить на конкретном станке. Поэтому приходится выбирать ближайшую (большую или меньшую) частоту вращения. Если же заданная скорость резания - предельная, то, чтобы ее не превысить, следует спуститься до ближайшей меньшей частоты - точки С. В этом случае происходит потеря скорости по сравнению с оптимальной, а это связано с потерей производительности обработки. Потери тем меньше, чем чаще наклонные линии на диаграмме, но это означает увеличение числа ступеней скорости на станке, а следовательно, - усложнение станка.

Важна также закономерность, согласно которой изменяется частота вращения при переходе с одной ступени на другую. В 1876 г. академик А.В. Гадолин обосновал целесообразность применения в станках геометрического ряда частот вращения шпинделей. Члены этого ряда составляют геометрическую прогрессию, соседние члены различаются в j раз, где j- знаменатель ряда. Следовательно;

n₁ = n_min ; n₂ = n₁ · j ; n₃ = n₂ · j = n₁ · j ² ;

n₄ = n₃ · j = n₁ · j³; ... ; n_z = n_z-1 · j = n₁ · j^z-1 = n_max.

Величину 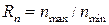называют диапазоном регулирования частот вращения шпинделя. Разделив выражение для n_max на n_min = n₁, получим .

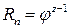Отрезок АС₃ на рис. 2.2. показывает абсолютную потерю скорости Dv, равную разности расчетной (оптимальной) v и фактической v_C скоростей: Dv= v - v_C. В рассматриваемом интервале частот вращения n₅ ... n₆ при заданном диаметре может произойти максимальная абсолютная потеря скорости Dv_max = v_B - v_C (отрезок B₃C₃, когда точка А близка к В). Если ряд - геометрический, то при одной и той же скорости v_B для различных частот вращения Dv_max оказывается величиной постоянной. т. е отрезки B₁C₁, B₂C₂, B₃C₃ и В₄С₄ равны.

Для всех интервалов ряда n максимальная относительная потеря скорости Dv_max / v = 1 - 1 / j. Так как j = const, то и Dv_max / v

= const. Постоянство возможной максимальной относительнои потери скорости при любых частотах является основным преимуществом геометрического ряда частот вращения и позволяет обоснованно планировать работу.

Значения знаменателей j рядов и ряды частот вращения стандартизованы ОСТ 2 Н11-1-72 (табл. 2.1). Можно продлить любой ряд, приведенный в таблице, путем умножения или деления табличных значений на 1000. Допускается отклонение фактических частот вращения на станке от табличных чисел на величину не более ± 10(j - 1)%.

Заметим, что при j = 1 регулирование бесступенчатое. При j_max=2 получается (D v/v)_max= 1 - 1/j = 1 - 1/2= 0,5, или 50 %. Из-за чрезмерно больших возможных потерь производительности не применяют j>2. Для станков чаще всего выбирают j = 1,26; 1,41; 1,58.

Все сказанное о рядах частот вращения шпинделей относится также к рядам скоростей подач и рядам чисел двойных ходов в 1 мин.