Исходя из вычисленных ранее по режимам обработки пределов частоты вращения шпинделя nmax и nmin и указанного в задании числа ступеней скорости Z, определяется значение знаменателя геометрического ряда j :
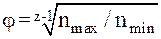 (2.6)
(2.6)
На основании этого вычисления по таблице 2.1 выбирается ближайшее стандартное значение знаменателя ряда.
Применение других значений j нецелесообразно в виду конструктивных трудностей в осуществлении негеометрических рядов в многоваловой шестеренной коробке.
Таблица 2.1
| Ряды предпочтительных чисел оборотов шпинделя , об./ мин. | ||||||
| Значение знаменателя ряда φ | ||||||
| (1,06) | 1,12 | 1,26 | (1,41) | 1,58 | (1,78) | (2) |
| 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 |
| 1,06 | ||||||
| 1,12 | 1,12 | |||||
| 1,18 | ||||||
| 1,25 | 1,25 | 1,25 | ||||
| 1,32 | ||||||
| 1,40 | 1,40 | 1,40 | ||||
| 1,50 | ||||||
| 1,60 | 1,60 | 1,60 | 1,60 | |||
| 1,70 | ||||||
| 1,80 | 1,80 | 1,80 | ||||
| 1,90 | ||||||
| 2,00 | 2,00 | 2,00 | 2,00 | 2,00 | ||
| 2,12 | ||||||
| 2,24 | 2,24 | |||||
| 2,36 | ||||||
| 2,50 | 2,50 | 2,50 | 2,50 | |||
| 2,65 | ||||||
| 2,80 | 2,80 | 2,80 | ||||
| 3,00 | ||||||
| 3,15 | 3,15 | 3,15 | 3,15 | |||
| 3,35 | ||||||
| 3,55 | 3,55 | |||||
| 3,75 | ||||||
| 4,00 | 4,00 | 4,00 | 4,00 | 4,00 | 4,00 | |
| 4,25 | ||||||
| 4,50 | 4,50 | |||||
| 4,75 | ||||||
| 5,00 | 5,00 | 5,00 | ||||
| 5,30 | ||||||
| 5,60 | 5,60 | 5,60 | 5,60 | |||
| 6,00 | ||||||
| 6,30 | 6,30 | 6,30 | 6,30 | |||
| 6,70 | ||||||
| 7,10 | 7,10 | |||||
| 7,50 | ||||||
| 8,00 | 8,00 | 8,00 | 8,00 | 8,00 | ||
| 8,50 | ||||||
| 9,00 | 9,00 | |||||
| 9,50 | ||||||
| 10,0 | 10,0 | 10,0 | 10,0 | 10,0 | ||
| 10,6 | ||||||
| 11,2 | 11,2 | 11,2 | ||||
| 11,8 | ||||||
| 12,5 | 12,5 | 12,5 | ||||
| 13,2 | ||||||
| 14,0 | 14,0 | |||||
| 15,0 | ||||||
| 16,0 | 16,0 | 16,0 | 16,0 | 16,0 | 16,0 | |
| 17,0 | ||||||
| 18,0 | 18,0 | 18,0 | ||||
| 19,0 | ||||||
| 20,0 | 20,0 | 20,0 | ||||
| 22,2 | ||||||
| 22,4 | 22,4 | 22,4 | ||||
| 23,6 | ||||||
| 25,0 | 25,0 | 25,0 | 25,0 | |||
| 26,5 | ||||||
| 28,0 | ||||||
| 30,0 | ||||||
| 31,5 | 31,5 | 31,5 | 31,5 | 31,5 | 31,5 | |
| 33,5 | ||||||
| 35,5 | 35,5 | |||||
| 37,5 | ||||||
| 40,0 | 40,0 | 40,0 | 40,0 | |||
| 42,5 | ||||||
| 45,0 | 45,0 | 45,0 | ||||
| 47,5 | ||||||
| 50,0 | 50,0 | 50,0 | ||||
| 53,0 | ||||||
| 56,0 | 56,30 | 56,0 | ||||
| 60,0 | ||||||
| 63,0 | 63,0 | 63,0 | 63,0 | 63,0 | 63,0 | |
| 67,0 | ||||||
| 71,0 | 71,0 | |||||
| 75,0 | ||||||
| 80,0 | 80,0 | 80,0 | ||||
| 85,0 | ||||||
| 90,0 | 90,0 | 90,0 | ||||
| 95,0 | ||||||
При выборе знаменателя геометрической прогрессии j необходимо учитывать следующее. Значение j = 1,26 является основным; применение же j < 1,26 не дает заметного повышения эксплуатационных возможностей станка, усложняет коробку скоростей и механизм управления для привода главного движения; знаменатели j = 1,41 и j = 1,58 следует использовать в станках, для которых особенно важно сокращение числа скоростей с целью упрощения и усовершенствования системы переключения и для которых нет необходимости точно выдерживать режимы резания ввиду кратковременности проходов. Так как в задании чаще всего задается значение Z , то расчетное значение j, как правило, не совпадает со стандартным. В таких случаях необходимо учитывать вышеизложенное. То есть допустим, что расчетное значение j получилось в пределах от 1,22 до 1,29, принимают j = 1,26. Если получилось j = 1,33 , т.е. среднее между 1,26 и 1,41, то, для станков универсального типа желательно уплотнить средние частоты вращения шпинделя (ЧНШ) за счет разряжения крайних. Тогда средние ЧВШ будут иметь j = 1,26 , а крайние j = 1,58 , т.е. в приводе используется ряд частот вращения с двумя знаменателями j (ломаный геометрический ряд).
Структурная формула
Коробки передач современных, особенно универсальных станков имеют большое число ступеней и большой диапазон регулирования скоростей. Они должны быть простыми и компактными, иметь малый вес, минимальное количество валов, передач, высокий к.п.д., низкий уровень шума. Конструкция коробок должна быть технологичной, надежной в эксплуатации, удобной в ремонте и обслуживании. Наиболее простыми по конструкции обычно бывают коробки передач с так называемой множительной структурой. Они состоят из элементарных двух- валовых механизмов, последовательно соединенных между собой. Число ступеней скорости, шпинделя Z при настройке последовательно включенными групповыми передачами (в многоваловых коробках) равно произведению чисел передач в каждой группе, т.е. Z = Pa·Pb·Pc·...·Pk
При заданном числе ступеней скорости шпинделя Z количество групп передач, количество передач в каждой группе и порядок положения групп может выбираться различным. Этот выбор в основном и определяет кинематику и конструкцию коробки скоростей. Для наиболее распространённых чисел ступеней скорости применяются конструктивные варианты, приведенные в таблице 2.2.
Количество конструктивных вариантов привода, состоящего из групп передач
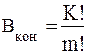 (2.7)
(2.7)
где K - количество групп передач,
m - количество групп с одинаковым числом передач.
Например, при K = 3 и m = 2 (Z = 12) количество конструктивных вариантов
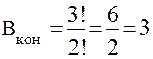 (2.8)
(2.8)
В зависимости от принятого порядка переключений группа может быть основной, первой, второй, третьей и последующей переборной. Основной и различными по номеру переборными группами может быть любая группа передач в приводе. Для определенного конструктивного варианта количество кинематических вариантов Вкин будет равно числу перестановок из числа К групп передач, т.е. Вкин = К! Например, для привода, состоящего из трех групповых передач Z = 3·2·2 , количество кинематических вариантов
Вкин = 3! = 6 .
Общее количество вариантов В = Вкин · Вкон .
Для рассмотренного примера В = 3 · 6 = 18. Необходимо сначала привести всевозможные структурные формулы, соответствующие данному числу ступеней Z скорости вращения шпинделя. Например, при Z = 12 это будут формулы: 3·2·2; 2·3·2; 2·2·3.
Затем из этих вариантов надо обоснованно выбрать один, наилучший и удовлетворяющий условиям задания, и для него привести всевозможные варианты развернутой структурной формулы. В развернутой структурной формуле, кроме числа передач, в группах указываются характеристики каждой группы (в скобках). Например, простая структурная формула 3·3 может быть реализована в виде двух развернутых структурных формул: 3[1] · 3[3] или 3[3] · 3[1]. Из всех вариантов развернутых структурных формул следует обоснованно выбрать оптимальный и удовлетворяющий условиям задания и в соответствии с ним изобразить структурную сетку привода главного движения.
Во избежание чрезмерно больших диаметров колес в коробках скоростей практикой установлены следующие предельные передаточные отношения imin ³ 1/4 и imax £ 2. Следовательно, наибольший диапазон регулирования групповой передачи:
Rп.пред = (imax/imin) = 2/1 · 4/1 = 8 .
Последняя переборная группа имеет наибольшую характеристику и диапазон регулирования, поэтому отношение (imax/imin)пред имеет наибольшую величину для последней переборной группы. Следовательно, для коробок скоростей (imax/imin)пред = jx max = 8 , где xmax - наибольший показатель для последней переборной группы.
Для нормализованных значений j максимально допустимые значения величины xmax для коробок скоростей приведены в табл.2.3.
Таблица 2.3
Максимально допустимые величины xmax
| j | 1,06 | 1,12 | 1,26 | 1,41 | 1,58 | 1,78 | |
| xmax |
2.4. Выбор наилучшего варианта кинематики
При выборе наилучшего варианта структурной сетки (варианта структурной формулы) необходимо учитывать следующее:
а) следует определить диапазон регулирования в последней переборной группе для всех вариантов структурных сеток (при выбранном значении j и исключить из дальнейщего рассмотрения варианты, не удовлетворяющие условию (imax/imin)пред = jx max £ 8 т.е. у которых xmax больше величины указaнной в табл.2.3 для заданного значения j . На структурной сетке xmax - это число интервалов между крайними лучами, исходящими из одной точки в последней переборной группе;
б) для уменьшения веса и габаритов привода число передач в группах должно уменьшаться от электродвигателя к выходному валу (шпинделю), т.е. Pa > Pb > Pc >..> Pk;
в) желательно, чтобы характеристики групп увеличивались от электродвигателя к шпинделю, т.е. если Z = Pa · Pb· Pc ·...Pk , то a < b < c < ...< k (веерообразная структурная сетка). В этом случае при одинаковых наименьших числах оборотов промежуточных валов для различных вариантов структурной формулы максимальные числа оборотов получаются меньшими, что уменьшает динамические нагрузки в передачах, вибрации, износ деталей и потери на трение, повышает к.п.д. при высоких числах оборотов шпинделя и дает возможность понизить требования к качеству изготовления деталей передач;
г) для того, чтобы наибольший диапазон регулирования групповой передачи, ограничивающий возможность конструктивного осуществления привода, подучился наименьшим, необходимо в качестве последней переборной группы брать группу с наименьшим числом передач;
д) лучше, если требуемое число ступеней Z получается меньшим числом групповых передач, т.к. в этом случае уменьшается количество валов, подшипников и отверстий в корпусе, повышается к.п.д. привода.
Дата: 2016-10-02, просмотров: 407.