При проектировании кинематической схемы коробок передач применяют аналитический и графо-аналитический методы. Последний метод предпочтительнее вследствие наглядности, удобства варьирования и уменьшения вероятности ошибок. При графо-аналитическом методе аналитически определяют диапазон регулирования частот вращения R_n число ступеней скорости z и число зубьев колес в передачах

Графическая часть метода состоит в построении структурной сетки и графика (картины) частот вращения с целью определения передаточных величин.

Построение ведут на базе логарифмической шкалы. Логарифмируя выражение n_z = n₁j^z-1, связывающее максимальную n_z и минимальную n₁ частоты вращения, получим:

lgn_z = lg n₁ + (z-1) lgj. (3.1)

Каждое деление шкалы (рис. 3.1) соответствует логарифму определенной частоты вращения, но около деления пишется значение этой частоты (или номер ступени скорости). Шкала разделена на z-1 интервалов, каждый из которых равен lgj .

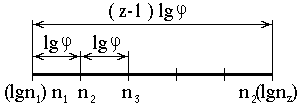
Рис. 3.1. Логарифмическая шкалa,

частот вращения

Таблица 3.1.

Характеристика групп

В коробке передач по рис. 3.4 p₁ = 4 - основная группа, а p₂ = 3 - первая переборная.

Кинематический порядок групп может не совпадать с порядком их конструктивного расположения. Оба порядка учитывают при составлении формулы структуры привода, которая для примера на рис. 3.4 записывается так: z = 12 = 4₁ · 3₂.

Каждый сомножитель означает число передач, составляющих группу. Порядок расположения сомножителей соответствует порядку расположения групп передач от двигателя к выходному валу (к шпинделю). Индексы у сомножителей показывают кинематический порядок.

3.1. Выбор структуры и построение структурных сеток.

При разработке кинематической схемы коробки передач, вычислив z, составляют формулу структуры, далее строят структурную сетку, а затем график частот вращения. Каждый шаг должен рассматриваться в вариантах, из которых один выбирают для проработки на последующем этапе.

Представим число ступеней z = 12 в виде произведения трех сомножителей: 2·2·3. Это означает, что должно быть три группы передач, порядок расположения и кинематический порядок которых следует выбрать.

Каждой выбранной формуле структуры однозначно соответствует структурная сетка, которая отличается от графика частот вращения прежде всего полной и обязательной симметричностью (в графике лишь некоторые лучи симметричны, причем это необязательно). Постоянные (одиночные) передачи в сетке не отражаются.

Пусть, например, выбрана структура z = 12 = 2₂ · 3₃ · 2₁. Для структурной сетки сначала проводят линии, соответствующие валам- на одну больше, чем число сомножителей в формуле структуры (число групп передач). Перпендикулярно проводят z линий по числу ступеней скорости (рис. 3.2). Сбоку пишут число передач p и характеристику хдля каждой группы (индексы у ри хпоказывают номер группы в конструктивном порядке расположения). В данном случае за основную группу принята группа с двойным блоком, расположенная в конце.

Построение структурной сетки начинают с точки 0 (рис. 3.2,а). Из каждой выделенной точки проводят симметрично столько лучей, сколько существует передач в данной группе, т.е. р, причем число интервалов шкалы между концами смежных лучей равно характеристике данной группы.

Структурная сетка не показывает частоты вращения и передаточные величины. Она отражает лишь соотношение между передаточными величинами в каждой группе, которое выражено уравнением (3.3). Характеристика каждой группы, а следовательно, число интервалов (lgj) между концами соседних лучей одинаковы в сетке и графике.

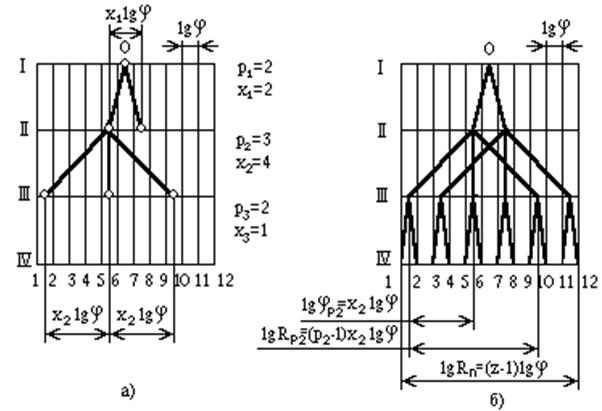
Рис. 3.2. Построение структурной сетки для z = 12 = 2₂ · 3₄ · 2₁:

а - начало построения; б - полная сетка

Структура z = 12 = 2₃ · 3₁ · 2₂ отличается от предыдущей только кинематическим порядком. Здесь основная группа находится в середине. Характеристики: х₁ = 6, х₂ = 1, х₃ = 3.

В структуре z = 12 = 3₁ · 2₂ · 2₃ (рис. 3.3) другой порядок расположения групп. Тройная передача оказалась в начале, но осталась основной. Характеристики: х₁ =1, х₂ =3, х₃ =6.

Общее число вариантов структур зависит от возможного числа перестановок в конструктивном и кинематическом порядках:

(К!)²/q!,

где К - общее число групп передач; q - число групп с равными числами передач.

При сравнении вариантов структурных сеток необходимо обращать внимание на размах крайних лучей, выходящих из одной точки (в каждой группе). Число интервалов lgj между концами таких лучейопределяет диапазон регулирования R_p в группе (характеристику группы) (см. рис. 3.2, б).

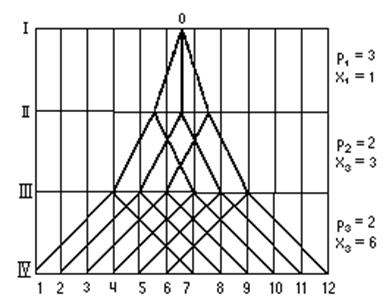
Рис. 3.3. Структурная сетка для z = 12 = 3₁ · 2₂ · 2₃ .

3.2.Описание готового графика частот вращения.

Для пояснения физического смысла элементов графика частот вращения рассмотрим график (рис. 3.4, б), соответствующий кинематической схеме коробки передач по рис. 3.4, а.

Горизонтальные линии, обозначенные римскими цифрами, соответствуют валам. Внизу изображена логарифмическая шкала частот вращения. Лучи между соседними горизонталями соответствуют передачам.

Совокупность передач, связывающих два соседних вала, называют группой передач. На рис. 10 показаны две группы передач: р₁ = 4 и р₂ = 3, где p - число передач, составляющих группу. Каждая выделенная на горизонталях точка показывает определенную частоту, с которой может вращаться вал. Так, частота вращения вала IV может меняться в диапазоне 315...630 мин^-1. Из каждой выделенной точки выходит к следующей горизонтали столько лучей, сколько передач в группе. Параллельные лучи в пределах группы соответствуют одной и той же передаче при различных включениях передач предшествующих групп (в данном примере при различных положениях двойных блоков.

Наклон луча и, следовательно, число перекрытых им интервалов логарифмической шкалы показывает передаточную величину передачи. Лучи, соответствующие повышающим передачам, наклонены в одну сторону (вправо - i'₅, i'₉), а соответствующие понижающим передачам - в другую сторону (влево - i'₂, i'₈ и др.).

Рис. 3.4. Кинематическая схема (а), график частот вращения (б) и структурная сетка (в) коробки передач .

Луч i'₅ отражает передачу, повышающую частоту вращения с 1000 (на валу 2) до 1250 мин^-1 (на валу 3). Этот луч перекрывает один интервал шкалы (lg j); следовательно, передаточная величина i'_s = j = 1,26. Передача с i'₄ = 1 не меняет скорость. Луч i'₃ отражает передачу, понижающую частоту вращения с 1000 до 800 мин^-1, причем i'₃ = 1/j = 1 / 1,25. Лучи i'₆ и i'₉ перекрывают по три интервала шкалы (3lg j), причем i'₉ = j³ = 1,26³ = 2 (повышающая передача) , i'₆ = 1/j³ = 1/1,26³ = 1/2 (понижающая переда).

3.4. Основные зависимости.

Чтобы ряд частот вращения шпинделя был геометрическим со знаменателем j, частота вращения каждого промежуточного вала должна изменяться по закону геометрической прогрессии, но со знаменателем j^x. Такому же закону должен подчиняться ряд передаточных величин в группе передач, что отражается следующим уравнением (без вывода):

i'₁ : i'₂ : i'₃ : ... : i'_p = 1 : j^x : j^2x : ... : j^(p-1)x , (3.3)

где x - характеристика группы передач (индексы y i' в данном уравнении не связаны с рис. 3.4,б). Действительно, для группы р₁ = 4 коробки передач по рис. 3.4,б

i'₂ : i'₃ : i'₄ : i'₅ = 1/j² : 1/j : 1 : j = 1 : j : j² : j³ т. е. x₁ = 1, а для группы р₂ = 3 по тому же рисунку : i'₇ : i'₈ : i'₉ = 1/j³ : 1/j : j³ = 1 : j⁴ : j⁵ ,т.е.

х₂ = 4. Характеристика показывает, сколько интервалов, равных lg j, между концами соседних лучей в группе передач на графике, т. е. она связывает знаменатель j ряда частот вращения на шпинделе и знаменатель j_p ряда передаточных величин в группе передач: j_p = j^x.

Значение характеристики зависит от так называемого кинематического порядка групп. Этот порядок определяет нарастание характеристики от группы к группе. Характеристика x_k для некоторой группы больше характеристики x_k-1 для группы, предшествующей в кинематическом порядке, в р_k-1 раз, где p_k-1 - число передач предшествующей группы: х_k = x_k-1 p_k-1. Согласно этому порядку одна из групп (любая) является основной, для нее х = 1. Следующую в кинематическом порядке группу передач называют первой переборной, далее идут вторая и другие переборные группы. Характеристика любой группы равна произведению чисел передач всех групп, предшествующих в кинематическом порядке, что показано в табл. 3.1.

При прямозубых колесах в коробке скоростей:

R_{p max} = i'_max : i'_min = 2 : 1/4 = 8.

Следовательно, каждому j соответствует максимально

допустимое число интервалов шкалы, охватываемых диапазоном регулирования R_p в группе:

j ... 1,12 1,26 1,41 1,58

[(p-1)x]_max ... 18 9 6 4

Варианты, не удовлетворяющие данному ограничению, следует не принимать во внимание при поиске формулы структуры.

Чтобы не приближаться к i'_max и i'_min, стремятся к структурам с меньшими R_p. Чтобы выдержать неравенство (2.5). R_p в последних группах должно быть больше, чем в первых.

Для выбора рациональной структуры привода не требуется пересматривать все возможные варианты структурных сеток. Уже при выборе формулы структуры надо руководствоваться следующими рекомендациями.

1. Группы с большим числом передач (три, тем более четыре) следует располагать ближе к двигателю, так как чем больше колес на быстроходных валах, тем больше выигрыш в массе деталей, габаритах узла.

2. В кинематическом порядке в качестве последней переборной группы обычно принимают группу с минимальным числом передач, иначе сочетание максимальной характеристики х и большого числа передач р может дать слишком большой диапазон регулирования R_p в группе.

3. Последнюю переборную группу следует располагать в конце структуры. В этой группе из-за большого диапазона регулирования передаточные величины близки к предельным, следовательно, неизбежна большая редукция, нежелательная в начале структуры.

Структура по рис. 3.3 удовлетворяет всем рекомендациям, однако она возможна только при j £ 1,41 (в противном случае R_p3 > 8). Структура по рис. 3.2, б при j = 1,41 неприемлема по той же причине. При j = 1,26 она возможна, но нерациональна, так как нарушены все рекомендации о порядке расположения групп и кинематическом порядке. Вообще, предпочтительны структуры, у которых в сетке лучи первых групп передач располагаются более компактно.