Одним з основних показників надійності є ймовірність безвідмовної

роботи, тобто ймовірність того, що в заданому проміжку часу відмов в системі не виникне

(4.1)

де Т – випадкова величина, яка характеризує час напрацювання системи до виникнення відмов;

- фіксований інтервал часу, наприклад (0; ).

Ймовірність виникнення відмов в системі називають ймовірністю того, що в період в ній обов’язково виникне відмова, тобто

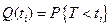. (4.2)

Оскільки система може знаходитись тільки в двох станах (працездатна та непрацездатна), то ці події складають повну групу несумісних подій, тому:

(4.3)

а

(4.4)

Фізичний зміст полягає в тому, що ця ймовірність характеризує частку працездатних виробів в момент часу .

Коли розглядають інтервал часу 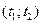, а не , тобто не з моменту включення системи, то мова йде про умовну ймовірність безвідмовної роботи в період 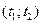. При цьому вважається, що система знаходилась в працездатному стані.

, (4.5)

де та 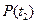- відповідно значення функції надійності на початку інтервалу і в кінці напрацювання.

Густина розподілу напрацювання до відмови – це похідна за часом від функції відмови

(4.6)

Цей показник характеризує безумовну ймовірність того, що система обов’язково відмовить в проміжку часу при умові, що в момент вона знаходилась в працездатному стані.

Найбільш поширеним кількісним показником надійності є інтенсивність відмов - тобто умовна ймовірність виникнення відмов в системі в деякий момент часу напрацювання при умові, що до цього моменту відмов у системі не було.

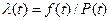. (4.7)

З фізичної точки зору інтенсивність відмов показує, яка частка всіх виробів або елементів даного типу в середньому стає непрацездатною за 1 годину роботи. Наприклад, якщо , то це означає, що за годину роботи із ладу вийде одна стотисячна частка елементів. За 1000 годин роботи можна очікувати, що непрацездатними стане одна сота долі всіх елементів. Тобто якщо в пристрої є 100 таких елементів, то в середньому за кожні 1000 годин із ладу виходе один елемент.

Значення довідкові для всіх відомих елементів .

Експериментально встановлено, що для більшості елементів, які використовуються в РЕА залежність 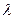від часу має такий вигляд:

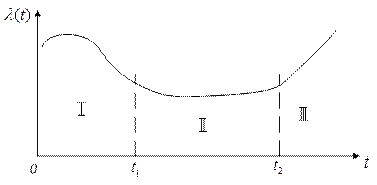
Рисунок 4.1– Залежність інтенсивності відмов від часу

На рисунку 4.1 час від початку роботи до називають періодом припрацювання (ранні відмови). З виходом із ладу таких елементів інтенсивність відмов зменшується і на інтервалі вважається, що вона майже постійна. Це період нормальної роботи і в цей час відбуваються, в основному, раптові відмови. Визначаючи надійність апаратури, необхідно врахувати, що використовуються такі значення інтенсивності відмов 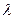, які мають місце в період нормальної роботи.

Інтервал часу після визначається закономірними процесами старіння та зносу матеріалів і елементів. В цей період відбуваються переважно поступові відмови.

В якості показника надійності систем також використовують середнє напрацювання до відмови − це математичне очікування напрацювання до першої відмови

(4.8)

зо своєю суттю Т_сер – середній час безвідмовної роботи, тобто час очікування нормальної роботи системи до першої відмови.

Одна із найважливіших формул теорії надійності не- відновлювальних систем – це залежність ймовірності безвідмовної роботи від інтенсивності відмов. Відомо, що

(4.9)

Звідси

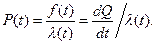(4.10)

Тоді (3.11)

Або , (4.12)

тобто (4.13)

Звідси (4.14)

Слід відзначити, що всі відмови протягом трьох станів (рисунок 4.1) носять випадковий характер. Тип розподілу випадкової величини напрацювання на відмову залежить від особливостей процесу розвитку відмови. Найбільш поширений закон розподілу відмов – це експоненціальний. По-перше, він характерний для складних систем, які складаються із різнорідних елементів з різними інтенсивностями відмов. По-друге, для цього закону отримані відносно прості форми для розрахунку надійності. Експоненціальний розподіл можна використовувати в тих випадках, коли нехтують впливом припрацювання, зносу та старіння. Тому цей закон найбільш точно описує відмови на другому етапі, тобто на етапі нормальної роботи. Оскільки вважається, що на цьому етапі , то основні показники надійності описуються такими формулами:

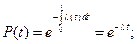(4.15)

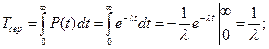(4.16)

Якщо апарат складається із nрізних елементів (блоків), то загальна інтенсивність відмов визначається як їх сума:

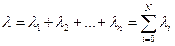(4.17)

Залежність ймовірності безвідмовної роботи від часу має експоненціальний вигляд (рисунок 4.2).

Значення площі під кривою загибелі визначає величину Т_сер. Маючи в своєму розпорядженні залежність (рис. 4.2), можемо з його допомогою визначити Т_сер . Для цього необхідно скористатись таким виразом:

(4.18)