http://www.matlab.mgppu.ru/work/0023.htm
По форме связь может быть линейной или нелинейной.
Таблица 1
| значение | интерпретация |
| до 0,2 до 0,5 до 0,7 до 0,9 свыше 0,9 | очень слабая корреляция слабая корреляция средняя корреляция высокая корреляция очень высокая корреляция |
Выбор метода вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные (см. таблицу 2).
Таблица 2
| Типы шкал | Мера связи | |
| Переменная X | Переменная Y | |
| Интервальная или отношений | Интервальная или отношений | Коэффициент Пирсона |
| Ранговая, интервальная или отношений | Ранговая, интервальная или отношений | Коэффициент Спирмена |
| Ранговая | Ранговая | Коэффициент Кендалла |
| Дихотомическая | Дихотомическая | Коэффициент φ, четырёхполевая корреляция |
| Дихотомическая | Ранговая | Рангово-бисериальный коэффициент |
| Дихотомическая | Интервальная или отношений | Бисериальный коэффициент |
| Интервальная | Ранговая | Не разработан |
с. 56 (64) 063.JPG
Коэффициент корреляции— двумерная описательная статистика, количественная мера взаимосвязи (совместной изменчивости) двух переменных.
История разработки и применения коэффициентов корреляции для исследования взаимосвязей фактически началась одновременно с возникновением измерительного подхода к исследованию индивидуальных различий — в 1870—1880 гг. Пионером в измерении способностей человека, как и автором самого термина «коэффициент корреляции», был Френсис Гальтон, а самые популярные коэффициенты корреляции были разработаны его последователем Карлом Пирсоном. С тех пор изучение взаимосвязей с использованием коэффициентов корреляции является одним из наиболее популярных в психологии занятием.
К настоящему времени разработано великое множество различных коэффициентов корреляции, проблеме измерения взаимосвязи с их помощью посвящены сотни книг. Поэтому, не претендуя на полноту изложения, мы рассмотрим лишь самые важные, действительно незаменимые в исследованиях меры связи — /--Пирсона, r-Спирмена и т-Кендалла'. Их общей особенностью является то, что они отражают взаимосвязь двух признаков, измеренных в количественной шкале — ранговой или метрической.
Вообще говоря, любое эмпирическое исследование сосредоточено на изучении взаимосвязей двух или более переменных.
Любое исследование можно свести к изучению корреляций, благо изобретены самые различные коэффициенты корреляции для практически любой исследовательской ситуации. Но в дальнейшем изложении мы будем различать два класса задач:
П исследование корреляций — когда две переменные представлены в числовой шкале;
□ исследование различий — когда хотя бы одна из двух переменных представлена в номинативной шкале.
Такое деление соответствует и логике построения популярных компьютерных статистических программ, в которых в меню Корреляции предлагаются три коэффициента (/--Пирсона, r-Спирмена и х-Кендалла), а для решения других исследовательских задач предлагаются методы сравнения групп.
ПОНЯТИЕ КОРРЕЛЯЦИИ
Взаимосвязи на языке математики обычно описываются при помощи функций, которые графически изображаются в виде линий. На рис. 6.1 изображено несколько графиков функций. Если изменение одной переменной на одну единицу всегда приводит к изменению другой переменной на одну и ту же величину, функция является линейной (график ее представляет прямую линию); любая другая связь — нелинейная. Если увеличение одной переменной связано с увеличением другой, то связь — положительная (прямая); если увеличение одной переменной связано с уменьшением другой, то связь — отрицательная (обратная). Если направление изменения одной переменной не меняется с возрастанием (убыванием) другой переменной, то такая функция — монотонная; в противном случае функцию называют немонотонной.
Функциональные связи,подобные изображенным на рис. 6.1, являются иде-ализациями. Их особенность заключается в том, что одному значению одной переменной соответствует строго определенное значение другой переменной. Например, такова взаимосвязь двух физических переменных — веса и длины тела (линейная положительная). Однако даже в физических экспериментах эмпирическая взаимосвязь будет отличаться от функциональной связи в силу неучтенных или неизвестных причин: колебаний состава материала, погрешностей измерения и пр.
В психологии, как и во многих других науках, при изучении взаимосвязи признаков из поля зрения исследователя неизбежно выпадает множество возможных причин изменчивости этих признаков. Результатом является то, что даже существующая в реальности функциональная связь между переменными выступает эмпирически как вероятностная (стохастическая): одному и тому же значению одной переменной соответствует распределение различных значений другой переменной (и наоборот). Простейшим примером является соотношение роста и веса людей. Эмпирические результаты исследования этих двух признаков покажут, конечно, положительную их взаимосвязь. Но несложно догадаться, что она будет отличаться от строгой, линейной, положительной — идеальной математической функции, даже при всех ухищрениях исследователя по учету стройности или полноты испытуемых. (Вряд ли на этом основании кому-то придет в голову отрицать факт наличия строгой функциональной связи между длиной и весом тела.)
Итак, в психологии, как и во многих других науках, функциональная взаимосвязь явлений эмпирически может быть выявлена только как вероятностная связь соответствующих признаков. Наглядное представление о характере вероятностной связи дает диаграмма рассеивания — график, оси которого соответствуют значениям двух переменных, а каждый испытуемый представляет собой точку (рис. 6.2). В качестве числовой характеристики вероятностной связи используются коэффициенты корреляции.
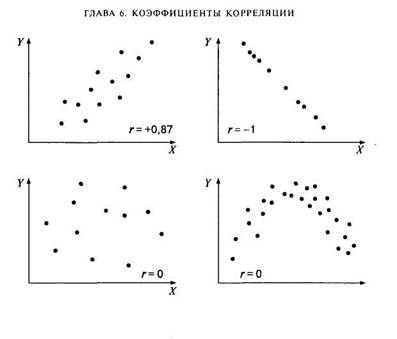
Рис. 6.2. Примеры диаграмм рассеивания и соответствующих коэффициентов корреляции
Коэффициент корреляции— это количественная мера силы и направления вероятностной взаимосвязи двух переменных; принимает значения в диапазоне от-1 до +1.
Сила связи достигает максимума при условии взаимно однозначного соответствия: когда каждому значению одной переменной соответствует только одно значение другой переменной (и наоборот), эмпирическая взаимосвязь при этом совпадает с функциональной линейной связью. Показателем силы связи является абсолютная (без учета знака) величина коэффициента корреляции.
Направление связи определяется прямым или обратным соотношением значений двух переменных: если возрастанию значений одной переменной соответствует возрастание значений другой переменной, то взаимосвязь называется прямой (положительной); если возрастанию значений одной переменной соответствует убывание значений другой переменной, то взаимосвязь является обратной (отрицательной). Показателем направления связи является знак коэффициента корреляции.
с. 70 (162)
Сравнение двух выборок по признаку, измеренному в метрической шкале, обычно предполагает сравнение средних значений с использованием параметрического критерия t-Стьюдента. Следует различать три ситуации по соотношению выборок между собой: случай независимых и зависимых выборок (измерений признака) и дополнительно — случай сравнения одного среднего значения с заданной величиной (критерий /-Стьюдента для одной выборки).
К параметрическим методам относится и сравнение дисперсий двух выборок по критерию F-Фишера. Иногда этот метод приводит к ценным содержательным выводам, а в случае сравнения средних для независимых выборок сравнение дисперсий является обязательной процедурой.
При сравнении средних или дисперсии двух выборок проверяется ненаправленная статистическая гипотезао равенстве средних (дисперсий) в генеральной совокупности. Соответственно, при ее отклонении допустимо принятие двусторонней альтернативы о конкретном направлении различий в соответствии с соотношением выборочных средних (дисперсий). Для принятия статистического решения в таких случаях применяются двусторонние критерии и, соответственно, критические значения для проверки ненаправленных альтернатив.
http://psystat.at.ua/publ/1-1-0-17 (очень доступно!!!)
Коэффициент корреляции является одним из самых востребованых методов математической статистики в психологических и педагогических исследованиях. Формально простой, этот метод позволяет получить массу информации и сделать такое же количество ошибок. В этой статье мы рассмотрим сущность коэффициента корреляции, его свойства и виды.
Слово correlation (корреляция) состоит из приставки «co-», которая обозначает совместность происходящего (по аналогии с «координация») и корня «relation» , переводится как «отношение» или «связь» (вспомним public relations – связи с общественностью). Дословно correlation переводится как взаимосвязь.
Коэффициент корреляции — это мера взаимосвязи измеренных явлений.
Коэффициент корреляции (обозначается «r») рассчитывается по специальной формуле и изменяется от -1 до +1. Показатели близкие к +1 говорят о том, что при увеличении значения одной переменной увеличивается значение другой переменной. Показатели близкие к -1 свидетельствуют об обратной связи, т.е. При увеличении значений одной переменной, значения другой уменьшаются.
Пример. На большой выборке был проведён тест FPI. Проанализируем взаимосвязи шкал Общительность, Застенчивость, Депрессивность.
Начнем с Застенчивости и Депрессивности. Для наглядности, задаём систему координат, на которой по X будет застенчивость, а по Y — депрессивность. Таким образом, каждый человек из выборки исследования может быть изображен точкой на этой системе координат. В результате расчетов, коэффициент корреляции между ними r=0,6992.

Как видим, точки (испытуемые) расположены не хаотично, а выстраиваются вокруг одной линии, причём, глядя на эту линию можно сказать, что чем выше у человека выражена застенчивость, тем больше депрессивность, т. е. эти явления взаимосвязаны.
Построим аналогичный график для Застенчивости и Общительности.
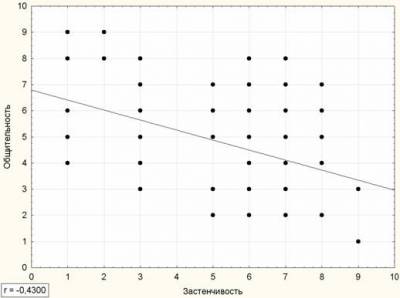
Мы видим, что с увеличением застенчивости общительность уменьшается. Их коэффициент корреляции -0,43.
Таким образом, коэффициент корреляции больший от 0 до 1 говорит о прямопропорциональной связи (чем больше… тем больше…), а коэффициент от -1 до 0 о обратнопропорциональной (чем больше… тем меньше…)
Если бы точки были расположены хаотично, коэффициент корреляции приближался бы к 0.
Коэффициент корреляции отражает степень приближенности точек на графике к прямой.
Приведём примеры графиков, отражающих различную степень взаимосвязи (корреляции) переменных исследования.
Сильная положительная корреляция:
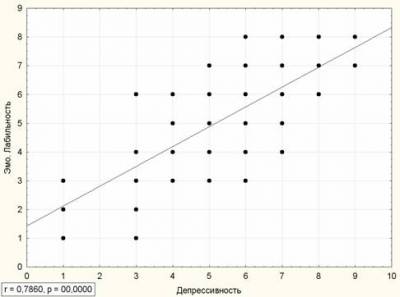
Слабая положительная корреляция:
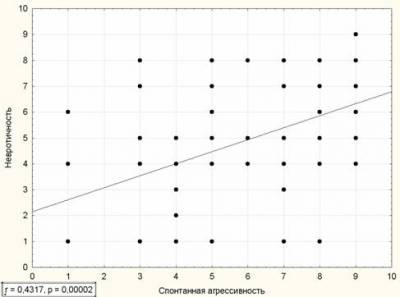
Нулевая корреляция:
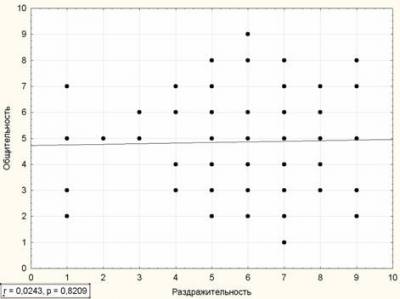
В подписи у каждого графика кроме значения r есть значение p. p – это вероятность ошибки, о которой будет рассказано отдельно.
Виды взаимосвязи
1. Прямая положительная и отрицательная взаимосвязь. Два явления непосредственно совпадают, поэтому взаимосвязаны. Интеллект и успеваемость в школе, общительность и застенчивость — яркие примеры прямой взаимосвязи.
2. Косвеная взаимосвязь. Два явления сильно коррелируют с третьим, поэтому между собой так же имеют корреляцию. К примеру, стиль общения ребенка взаимосвязан со стилем воспитания в семье за счет третьей переменной — установок личности. Очевидно, что воспитание в семье формирует установки ребенка, в свою очередь установки влияют на поведение.
3. Нулевая корреляция. Предполагает отсутствие закономерной взаимосвязи между переменными.
4. Случайная взаимосвязь. Корреляция может быть случайной! Очень многие процессы происходят одновременно и совпадают. Здесь уместно сказать, что если много-много коррелировать — что нибудь обязательно скоррелируется.
Важно. Взаимосвязь должна интерпретироваться в оба направления. Формально, корреляция не обозначает причинно-следственной связи! Это ВЗАИМОсвязь, ВЗАИМОсовпадение, явлений. Возвращаясь к примеру: застенчивость взаимосвязана с депрессивностью. Логично подумать, что депрессивный человек более застенчив, чем не депрессивный, но почему не наоборот? С чего начинать рассуждение? Мы интерпретируем корреляцию в оба направления и не констатируем причинно-следственную связь. Пишем «кореляция», «взаимосвязь», подразумеваем – совпадение. Причем сильная корреляция обозначает неслучайное совпадение.
Есть случаи, когда корреляция может говорить о причинно следственной связи. Это случаи, когда одна из переменых общективна, а вторая субъективна. К объективным переменным относятся возраст, стаж, рост, которые просто не могут зависеть от субъективных переменных: настроения, особенностей личности, мотивации и т.д. Однако, такие объективные переменные, как вес, количество детей в семье, частота смены места работы, количество контактов и т.п. могут и часто зависят от субъективных психологических показателей.
К примеру, профессионализм рабочего повышается со стажем. Стаж и профессионализм коррелируют и мы можем быть уверены, что для повышения профессионализма стаж является объективной причиной. Объективные переменные, основанные на времени всегда являются причиной при наличии корреляции с субъективными характеристиками. В остальных случаях нужно очень осторожно относиться к причинно-следственным интерпретациям коэффициента корреляции.
Если причинно-следственная связь обоснована в теоретической части работы и подтверждается многими авторами, то корреляцию так же можно интерпретировать как причинно-следственную связь.
Существуют различные формулы расчета коэффициента корреляции для различных типов шкал (см. статью «Понятие переменной и шкалы измерения»). Результатом расчета по любой формуле будет число от -1 до +1.
В следующей таблице написаны названия коэффициентов корреляции для различных типов шкал.
| Дихотомическая шкала (1/0) | Ранговая (порядковая) шкала | Интервальная и абсолютная шкала | |
| Дихотомическая шкала (1/0) | Коэфициент ассоциации Пирсона, коэффициент четырехклеточной сопряженности Пирсона. | Рангово-бисериальная корреляция. | Бисериальная корреляция |
| Ранговая (порядковая) шкала | Рангово-бисериальная корреляция. | Ранговый коэффициент корреляции Спирмена или Кендалла. | Значения интервальной шкалы переводятся в ранги и используется ранговый коэффициент |
| Интервальная и абсолютная шкала | Бисериальная корреляция | Значения интервальной шкалы переводятся в ранги и используется ранговый коэффициент | Коэффициент корреляции Пирсона (коэффициент линейной корреляции) |
Основные принципы интерпретации различных коэффициентов корреляции одинаковы. В случае дихотомической шкалы мы говорим о вероятности совпадения (прямого или обратного) ответов типа да/нет, в случае рангов о вероятности совпадения порядка, в случае коэффициента линейной корреляции мы говорим о степени совместного изменения переменных или о их взаимосвязи.
Полученный коэффициент нужно проверить на значимость, которая зависит от вероятности ошибки и количества человек. Коэффициент корреляции может быть формально небольшим, к примеру r=0,17, но если исследование проведено на 500 человек и вероятность ошибки (р) менее 0,05, то мы признаём значимым даже такой небольшой коэффициент. С другой стороны, при выборке в 5 человек очень большой коэффициент мы признаем незначимым, т.к. из-за малого количества человек мы можем совершить ошибочный вывод об этой корреляции.
Таким образом, для нас главное узнать какой должна быть вероятность ошибки и количество человек, чтобы признать полученный коэффициент действительно значимым.
Расчет значения р (вероятности ошибки) – сложная процедура, поэтому компьютерные программы, в которых можно считать коэффициент корреляции, расчитывают вероятность ошибки самостоятельно. Если же расчет производился вручную или по другим причинам конкретное значение р неизвестно, то используем уже рассчитанные таблицы критических значений.
Таблицы критических значений предназначены чтобы можно было найти критическое значение коэффициента корреляции, т.е. такое, после которого взаимосвязь можно считать значимой и неслучайной. При этом значение вероятности ошибки задаётся исследователем. В таблицах обычно есть критические значения коэффициентов корреляции для р≤0,001, р≤0,01, р≤0,05, иногда пишут соответственно 0,1%, 1%, 5%. Таким образом, пользуясь таблицами мы отвечаем на вопрос: какое критическое значение коэффициента корреляции при данном количестве людей и вероятности ошибки менее или равно 0,1% (1%, 5%)?
Обычно в психологических исследованиях вероятность ошибки выбирают на уровне p≤0,05, но если в исследовании принимают участие более 100 человек, то можно выбирать и р≤0,01. В первой колонке таблицы критических значений находится значение df (Degrees of Freedom — степени свободы), которое расчитывается очень просто: df = n-1, где n – количество человек. На пересечении нужного df и выбранной вероятности ошибок находим критический коэффициент корреляции. Если рассчитанное значение больше критического — коэффициент значимый, в обратном случае взаимосвязь является случайной.
В примерах, приведённых выше для количества человек n=89 и p≤0,05 критический коэффициент корреляции r=0,20. А вот если бы количество человек было 45 (при том же p≤0,05) то критическим значением было бы r=0,29, при количестве человек 10 критическое значение r=0,63.
Вывод
Коэффициент корреляции — это мера взаимосвязи измеренных явлений. На самом примитивном уровне его можно рассматривать как меру совпадения двух рядов чисел. Любой коэффициент корреляции изменяется в пределах от -1 до +1. Отрицательные значения говорят про обратнопропорциональную взаимосвязь, положительные о прямопропорциональной. Полученный коэффициент необходимо сравнивать с критическим табличным.
Дата: 2016-10-02, просмотров: 560.