
Конечно, таблицы сопряженности могут включать номинативные признаки, имеющие и более двух градаций. Например, по табл. 3.1 для изучения различий в самооценке мальчиков и девочек исследователь мог бы построить таблицу сопряженности признаков «Пол» (две градации) и «Самооценка» (пять градаций).
с. 40 (132)
Анализ таблиц сопряженности применяется для решения задач, которые могут быть сформулированы следующим образом:
1. Необходимо сравнить два (или более) распределения между собой.
Например, различаются ли мужчины и женщины по распределению предпочтений пяти политических лидеров?
2. Необходимо определить связь между двумя номинативными признака
ми (между классификациями объектов по двум разным основаниям).
Например, связано ли соотношение предпочтений трех групп напитков (соки, лимонады, минеральные воды) с сезонностью (зима, весна, лето, осень)?
Нетрудно заметить, что эти задачи отличаются лишь словесными формулировками. Так, изучение связи между двумя номинативными переменными тождественно сравнению градаций одной номинативной переменной по распределению другой номинативной переменной.
Например, изучать сезонную зависимость предпочтений различных напитков — то же самое, что сравнивать сезоны по распределению предпочтений этих напитков. А изучать связь двух оснований классификации респондентов — по полу и по политической ориентации — то же самое, что сравнивать распределение мужчин и женщин по политической ориентации.
В подобных случаях подразумевается анализ таблиц сопряженности, в которых столбцы соответствуют сравниваемым распределениям (градациям одной номинативной переменной), а строки соответствуют градациям сравниваемых распределений (градациям другой номинативной переменной).
Формулировка проверяемой Но: классификация объектов (людей, событий) по одному основанию не зависит от их классификации по другому основанию.
Исходные данные: определена принадлежность каждого объекта выборки к одной из градаций первой номинативной переменной и к одной из градаций второй номинативной переменной. Иными словами, две номинативные переменные измерены на выборке объектов. Строки таблицы сопряженности соответствуют градациям одной номинативной переменной, столбцы — градациям другой номинативной переменной.
Если проверка содержательной гипотезы предполагает анализ таблицы сопряженности, то принципиальным является вопрос о размерности таблицы. Будем различать два случая:
П общий случай (число градаций хотя бы одного из признаков больше 2-х),
О частный случай: таблицы сопряженности 2x2 (по две градации для каждой переменной).
Эти случаи различаются как порядком расчетов, так и особенностями интерпретации.
(начало можно посмотреть в вопросах №№ 34 и 35)с. 76 (82)
с. 77 (83) 082.JPG
Таблица сопряженности 2x2
| Признак X | Итог | |||
| Признак Y | а | Ъ | а+ b | |
| с | d | с + d | ||
| Итог | а + с | b + d | N |
Вэтом случае допустимо применение г-Пирсона (формула 6.1) непосредственно к исходным данным — двум бинарным переменным, принимающим значение 0 или 1, измеренным для каждого члена выборки численностью Л'. Результат применения r-Пирсона к двум бинарным переменным называется «фи-коэффициентом сопряженности» (Phi). Если данные представлены в четырех-клеточной таблице сопряженности, то применяется формула, существенно упрощающая расчеты, но дающая аналогичный результат:
ad-bc c
ср = ■ , (6.10)
J(a + b)(c + d)(a + c)(b + d) где а, Ь, с, d соответствуют обозначениям в четырехклеточной таблице 6.1.
ПРИМЕР 6.7__________________________________________________
Исследовалась связь семейного положения студенток (X: 0 — холостая, 1 — замужем) и их академической успеваемости (Y: 0 — закончила вуз, 1 — отчислена). В распоряжении исследователя есть данные для 12 студенток:
| № | ||||||||||||
| X | ||||||||||||
| Y |
Таблица сопряженности для этих данных:
| X | Итог | |||
| Y | ||||
| Итог |
http://psystat.at.ua/publ/drugie_vidy_koehfficienta_korreljacii/1-1-0-38
Если обе переменные представляют собой дихотомическую шкалу то следует использовать коэффициент четырехклеточной сопряженности Пирсона.
Классификация объектов по дихотомической шкале приведет к построению четырехклеточной таблицы.
К примеру, студент может посетить более 50% лекций, а может и не посетить, может сдать зачет с первого раза, а может и не сдать. На основе такой классификации построим таблицу:
| Сдал зачет с первого раза | Не сдал зачет с первого раза | |
| Студент посещал лекции | a | b |
| Студент не посещал лекции | c | d |
В клетки a,b,c,d таблицы следует вписать количество объектов, обладающих соответствующими признаками.
Формула расчета коэффициента четырехклеточной сопряженности Пирсона:
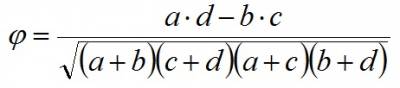
Приведенный коэффициент является ни чем иным, как модификацией коэффициента корреляции Пирсона, поэтому так же изменяется от - 1 до + 1 и критические значения этого коэффициента даны в таблице критических значений для коэффициента Пирсона.
Коэффициент четырехклеточной сопряженности часто применяется для коррелирования ответов на вопросы теста, закодированные в дихотомической шкале.
Дата: 2016-10-02, просмотров: 373.