Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Метод позволяет проверить гипотезу о том, что средние значения двух ie-неральных совокупностей, из которых извлечены сравниваемые зависимые вы­борки, отличаются друг от друга. Допущение зависимости чаще всего значит, что признак измерен на одной и той же выборке дважды, например, до воз­действия и после него. В общем же случае каждому представителю одной вы­борки поставлен в соответствие представитель из другой выборки (они по­парно объединены) так, что два ряда данных положительно коррелируют друг с другом. Более слабые виды зависимости выборок: выборка 1 — мужья, вы­борка 2 — их жены; выборка 1 — годовалые дети, выборка 2 составлена из близнецов детей выборки 1, и т. д.

Проверяемая статистическая гипотеза, как и в предыдущем случае, Н₍₎: М] = М₂. При ее отклонении принимается альтернативная гипотеза о том, что М_{ больше (меньше) М₂.

Исходные предположения для статистической проверки:

П каждому представителю одной выборки (из одной генеральной совокупно­сти) поставлен в соответствие представитель другой выборки (из другой генеральной совокупности);

D данные двух выборок положительно коррелируют;

О распределение изучаемого признака и в той и другой выборке соответству­ет нормальному закону.

Структура исходных данных: имеется по два значения изучаемого признака для каждого объекта (для каждой пары).

Ограничения: распределения признака и в той, и в другЪй выборке суще­ственно не отличаются от нормального; данные двух измерений, соответству­ющих той и другой выборке, положительно коррелируют.

Альтернативы: критерий Г-Вилкоксона, если распределение хотя бы для одной выборки существенно отличается от нормального; критерий ?-Стьюдента для независимых выборок — если данные для двух выборок не корре­лируют положительно.

Формула для эмпирического значения критерия /-Стьюдента отражает тот факт, что единицей анализа различий является разность (сдвиг) значений при­знака для каждой пары наблюдений. Соответственно, для каждой из N пар значений признака сначала вычисляется разность d_t = х_и — x_2i

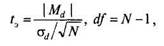где M_d ~~ средняя разность значений; a_d — стандартное отклонение разностей.

Замечание. В отношении зависимых выборок вполне допустимо при­менение критерия /-Стьюдента для независимых выборок (но не наоборот!). Это целесообразно, если корреляция между двумя измерениями отрицатель­ная. Если же корреляция положительная, то такая замена приведет к недо­оценке достоверности различий.

 

titkova-matmetody.pdf с. 64

t-Критерий Стьютдента используется для:

1) установления сходства-различия средних арифметических значений в двух выборках

( 1 M ↔ 2 M ) или в более общем виде, для установления сходства-различия двух эмпирических

распределений;

2) установления отличия от нуля некоторых мер связи: коэффициента линейной

корреляции Пирсона, ранговой корреляции Спирмена, точечно-бисериальной и рангово-

бисериальной корреляции (rxy, rs, rpb ↔”0” ) и коэффициента линейной регрессии (Rху ↔ "О"):

3) установления сходства-различия двух дисперсий в двух зависимых выборках.

Ограничения:

1) это параметрический критерий, поэтому необходимо, чтобы распределение признака, по

крайней мере, не отличалось от нормального распределения;

2) для независимых и зависимых выборок разные формулы расчета;

Гипотезы

1) независимые выборки:

Н0: средние значения признака в обоих выборках не различаются,

Н1: средние значения признака в обоих выборках статистически значимо различаются.

2) зависимые выборки:

Н0: разности оценок испытуемых в двух состояниях не отличаются от нуля,

Н1: разности оценок испытуемых в двух состояниях статистически значимо отличаются от

нуля.

Рассмотрим случай 1.

Пример 5.1.(независимые выборки). Предположим, имеется две независимые выборки

школьников, интеллект которых развивали в течение некоторого времени по двум различным

методикам, требуется установить, какая из методик лучше (табл.5.1). Предварительно было выяснено, что начальный уровень интеллекта был одинаковым в обеих выборках. Задача

сравнения двух методик может быть переформулирована на язык статистики как задача сравнения

средних арифметических значений интеллекта в обеих выборках.

Гипотезы:

Н0: средние значения уровня интеллекта в обоих выборках не различаются,

Н1: средние значения уровня интеллекта в обоих выборках статистически значимо

различаются.

В данном случае для получения эмпирического значения t-критерия используется

следующая формула:

где: n1, n2 – количество испытуемых в 1-й и 2-й выборках; 2 1 ,M M – средние

арифметические значения в 1-й и 2-й выборках; σ1, σ2 – стандартные отклонения в 1-й и 2-й

выборках.

Количество степеней свободы для нахождения критического значения критерия:

Df = n1+n2-2.

(В рассматриваемых примерах критические значения t-критерия приводятся для

ненаправленных гипотез).

Тогда:

 

Таким образом, получаем tэмп=2,486

Критические значения t-критерия находим по таблице 1 (приложение 5.3.) для df=30+32-

2=60.

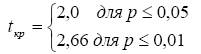
Полученное эмпирическое значение t-критерия превышает критическое для α=0,05, но

оказывается меньше критического для α=0.01, т.е.

2,0<Tкр=2,486 < 2,66

Вывод: Н0 гипотеза отклоняется и можно сделать вывод о статистически значимом

различии средних арифметических значений в двух выборках для ρ≤0.05 и о преимуществах

второй методики по сравнению с первой.

Строгое использование t-критерия предполагает, что обе выборки извлечены из

нормальных совокупностей. Однако многие авторы не считают это условие достаточно жестким,

указывая на возможность использования t-критерия в ситуациях, когда нет серьезных оснований

сомневаться в нормальности распределения признака в генеральной совокупности, даже если это

нельзя подтвердить статистически.

При зависимых выборках возникает корреляция результатов, поскольку измерения

проводятся на одних и тех же испытуемых в различных условиях (х и у)', чтобы учесть влияние

корреляции, применяется другая формула:

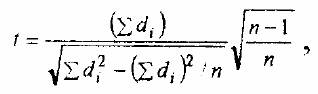
где di = xi – уi, то есть разность значений признака для каждого испытуемого. Количество

степеней свободы df=n–1. Проверяется статистическая гипотеза о соответствии распределения

разностей t-распределению Стьюдента с нулевым средним значением.

Пример 5.2. (зависимые выборки). Допустим, проводится измерение ситуативной

тревожности до и после психотерапевтического воздействия с помощью некоторого опросника

(табл.5.2). Исследователя интересует вопрос, приводит ли воздействие к изменению уровня

тревожности.

Гипотезы:

Н0: разности оценок у испытуемых ситуативной тревожности до и после

психотерапевтического воздействия не отличаются от нуля,

Н1: разности оценок у испытуемых ситуативной тревожности до и после

психотерапевтического воздействия статистически значимо отличаются от нуля

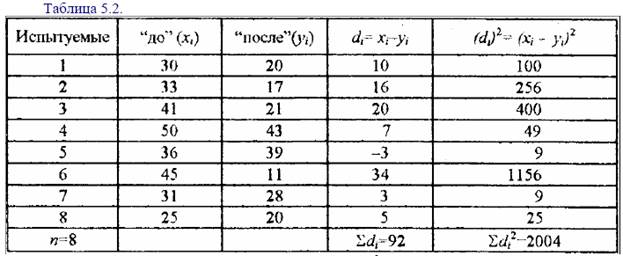
Подставив в формулу найденные значения Σdi и Σdi² получим:

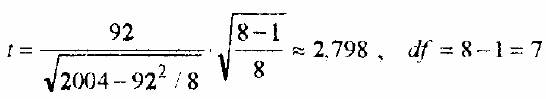
Имеем: tэмп=2,798

Находим по таблице 1 критические значения (Приложение 5.3.)

Отсюда: 2,365<tэмп=2,798<3,499

Вывод: Принимается Н1 гипотеза. Различия в уровнях тревожности до и после

психотерапевтического воздействия следует признать статистически значимыми (р<0,05), так как

эмпирическое значение превышает первое критическое, но меньше второго. Следовательно,

психотерапевтическое воздействие действительно снижает тревожность.

26. t-критерий Стьюдента. Применение критерия для установления различия (сходства) дисперсий в двух зависимых выборках.

titkova-matmetody.pdf с. 64 (начало см. в вопросе №25)

(для дисперсий пока не найдено, но может быть, это конец фрагмента titkova-matmetody.pdf с. 64 из вопроса № 25, со слов Пример 5.2. (зависимые выборки))

(ответ, может быть, у Наследова на страницах 164-169)

F-критерий Фишера.

titkova-matmetody.pdf с. 67

F-критерий Фишера используется для:

1) установления сходства-различия дисперсий в двух независимых выборках (D1↔D2);

2) установления отличия от нуля коэффициента детерминации (η2 ↔"О");

3) установления наличия-отсутствия влияния фактора в дисперсионном анализе.

Случай 1

Эмпирическое значение F-критерия для сравнения двух дисперсий в независимых

выборках находят по очень простой формуле:

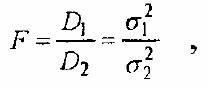
где D1 – большая дисперсия, D2 – меньшая дисперсия [Подстановка в числитель большей

дисперсии необходима для использования таблиц критических значений, в которых приводится

только правое критическое значение (больше единицы). Статистические программы рассчитывают

и левое критическое значение (меньше единицы)].

Количество степеней свободы определяется отдельно для числителя и отдельно для

знаменателя:

dfчисл= nчисл-1

dfзнам =nзнам -1

Пример 5.3.Две группы испытуемых обучались некоторым моторным навыкам по двум

разным методикам, фиксировалось количество ошибочных действий, до обучения результаты в

обеих группах имели одинаковый разброс. Какая из методик даст наибольшее выравнивание

результатов внутри группы после обучения (табл.5.3.).

Подставляя в формулу получим:

Fэмп= 36/16 = 2,25.

dfчисл= 16-1 = 15

dfзнам =21-1 = 20

Поскольку нам заранее не известно, какая из методик может обладать меньшей

дисперсией, мы используем ненаправленную гипотезу и, следовательно, двусторонний критерий.

Находим по таблице 3 (Приложение) критическое значение Fкр для α = 0,05 (α/2+α/2 = 0,05) и

dfчисл=15, dfзнам=20, Fкрит=2,573.

Получим: Fэмп=2,25∠Fкрит=2,573

Вывод: Так как эмпирическое значение меньше критического, то статистически значимых

различий дисперсий в первой и второй группах нет и, следовательно, стабилизация навыка при

обучении по обеим методикам одинакова.

Замечание. Для сравнения дисперсий в зависимых выборках более строгим будет

применение t-критерия Стьюдента.

Случай 2

В случае определения отличия от нуля коэффициента детерминации эмпирическое

значение F-критерия рассчитывается так:

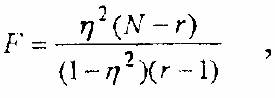
где: N – общее число испытуемых, r-число интервалов квантования, исходя из которых

рассчитывалось η2.

При определении критического значения число степеней свободы для числителя:

dfчисл=r–1,

для знаменателя:

dfзнам=N–r.

(Коэффициент детерминации – η2, определяет общую меру связи – корреляционное

отношение. Он определяется по формуле:

Здесь:

SSвнтр – сумма квадратов отклонений от внутригруппового (условного) среднего;

SSобщ – сумма квадратов отклонений от общего для всех измерений среднего (безусловного

среднего);

Следует отметить, что в отличие от линейной корреляции коэффициент детерминации

устанавливает два типа связей: зависимость х от у и зависимость у от х (η2

х/у, η2

у/х). То есть сначала

одна переменная рассматривается как зависимая, другая – как независимая, затем наоборот).

Пример 5.4.В таблице 5.4. даны результаты тестирования по двум методикам 12

испытуемых. Отличается ли коэффициент детерминации от нуля?

В нашем случае, имеем η2=0,77, N=12, r=4. Подставляя в формулу,

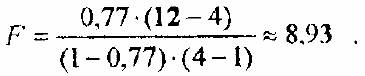
получаем Fэмп=8,93.

Критические значения F-кpитepия для α =0,05, dfчисл=4-1=3, dfзнам=12-4=8 находим по

таблице:

Fэмп=8,93>Fкр(ρ≤0,01)=7,591

Вывод: Коэффициент детерминации η2 статистически значимо отличается от нуля

(ρ<0.01).

U-критерий Манна-Уитни.

090309-matmetody.txt

Если две независимые выборки, и распределение отличается от нормального - пользуемся критерием Манна-Уитни. Непараметрический метод сравнения выборок.

с. 81 (173)

Самым популярным и наиболее чувствительным (мощным) аналогом кри­терия f-Стьюдента для независимых выборок является критерий U-Манна-Уитни (Mann-Whitney U). Непараметрическим его аналогом является критерий серий (см. главу 8), который еще проще в вычислительном отношении, но обладает заметно меньшей чувствительностью, чем критерий U.

Эмпирическое значение критерия tZ-Манна-Уитни показывает, насколько совпадают (пересекаются) два ряда значений измеренного признака. Чем мень­ше совпадение, тем больше различаются эти два ряда. Основная идея критерия Uоснована на представлении всех значений двух выборок в виде одной общей последовательности упорядоченных (ранжированных) значений. Основной (нулевой) статистической гипотезе будет соответствовать ситуация, когда зна­чения одной выборки будут равномерно распределены среди значений другой выборки, то есть когда два ряда значений пересекаются в наибольшей возмож­ной степени. Напротив, отклонению этой гипотезы будет соответствовать си­туация, когда значения одной из выборок будут преобладать на одном из кон­цов объединенного ряда — пересечение двух рядов тогда будет минимальным.

ПРИМЕР 12.1_____________________________________________________

Обозначим значения переменной для одной выборки X, а для другой выборки — У и упорядочим значения обеих выборок по возрастанию.

 

Значения

Выборка

X

X

У

X

X

X

У

X

X

У

X

У

У

Y

У

У

Значения одной выборки распределены явно не равномерно среди значений дру­гой выборки: значения выборки У преобладают на правом конце объединенного ряда. Однако критерий серий не позволяет обнаружить статистически значимые различия: всего серий в данном случае W— 8 и при т = п = $ эта величина не выхо­дит за пределы критических значений для а = 0,05 (приложение 5).

Формально, критерий U— это общее число тех случаев, в которых значе­ния одной группы превосходят значения другой группы, при попарном срав­нении значений первой и второй групп. Соответственно, вычисляются два значения критерия: U_x и U_y.

Для вычислений «вручную» используются следующие формулы: (172.JPG)

где п — объем выборки X; m — объем выборки У, R_x и R_y — суммы рангов для X и У в объединенном ряду. В качестве эмпирического значения критерия бе­рется наименьшее из U_x и U_y. Чем больше различия, тем меньше эмпирическое значение U.

Поскольку критерий U отражает степень совпадения (перекрещивания) двух рядов значений, то значениер-уровня тем меньше, чем меньше значение U. При расчетах «вручную» используют таблицы критических значений крите­рия £/-Манна-Уитни (приложение 9).

ПРИМЕР 12.1 (продолжение)

Проверим гипотезу о различии выборок X (численностью т = 8) и К (численно­стью п = 8) на уровне а = 0,05:

 

Значения

Выборка

X

X

Y

X

X

X

Y

X

X

Y

X

Y

Y

Y

Y

Y

Ранги

Ранги X

Ранги Y

5, ^9

Ш а г 5. Определяется/7-уровень значимости: наименьшее из f/сравнивается с таб­личным (приложение 9) для соответствующих объемов выборки т = 8 и п = 8. Зна­чение р < 0,05 (0,01), если вычисленное £/_энп < £/_табл В нашем случае наименьшим является U_y = 10, которое и принимается за эмпирическое значение критерия. Оно меньше критического для р = 0,05 (U= 13) , но больше критического для р = 0,01 (U=7). Следовательно,/? < 0,05.

Ш а г 6. Принимается статистическое решение и формулируется содержательный вывод. На уровне а = 0,05 принимается статистическая гипотеза о различии Xи Y по уровню выраженности признака. Уровень У статистически достоверно выше уров­ня Х(р< 0,05).

Замечание. Связи в рангах для вычислений «вручную» не предусмот­рены. Хотя они и незначительно влияют на результат, но если доля одинако­вых рангов по одной из переменных велика, то предлагаемый алгоритм не­применим, пользуйтесь компьютерной программой (SPSS, Statistica).

T-критерий Вилкоксона.

с. 84 (176)