Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

План работы

 

Вопросы к экзамену. 1

21. Виды статистических гипотез. 1

22. Виды статистических критериев. Порядок проверки статистических гипотез с помощью статистических критериев. 4

23. Ошибки первого и второго рода. Доверительная вероятность. 8

24. Мощность критерия. 9

25. t-критерий Стьюдента. Применение критерия для установления различия (сходства) средних арифметических значений в 2-х выборках. 10

26. t-критерий Стьюдента. Применение критерия для установления различия (сходства) дисперсий в двух зависимых выборках. 14

27. F-критерий Фишера. 14

28. U-критерий Манна-Уитни. 16

29. T-критерий Вилкоксона. 17

30. L-критерий Пейджа. 22

31. χ2-критерий Пирсона. Применение критерия для установления сходства-различия между эмпирическим и равномерным распределением. 26

32. χ2-критерий Пирсона. Применение критерия для установления сходства-различия между эмпирическим и нормальным распределением. (???чем этот вопрос отличается от № 31???) 34

33. χ2-критерий Пирсона. Оценка значимости отличия от нуля коэффициентов сопряженности φ, К_ч и С. 35

34. Таблицы сопряженности. Коэффициент четырехклеточной сопряженности Пирсона. 36

35. Таблицы сопряженности. Коэффициенты многоклеточной сопряженности Чупрова и Пирсона. 39

36. Основные характеристики корреляционной связи. Общая и частная классификации корреляционной связи. (???что подразумевается под классификаией???) 40

37. Коэффициент ранговой корреляции Спирмена. 47

Ранговые коэффициенты корреляции по Спирману и Кендалу. 49

38. Точечно-бисериальный коэффициент корреляции. 51

39. Рангово-бисериальный коэффициент корреляции. 53

40. Коэффициент линейной корреляции. 54

41. Корреляционная матрица и корреляционный граф. 57

Вопросы к экзамену

Мощность критерия.

Мощность критерия. Важнейшей характеристикой любого статистического критерия

является его мощность.

Мощность критерия – это его способность выявлять различия, если они есть. Иначе, это

его способность отклонить нулевую гипотезу об отсутствии различий, если она неверна.

(отсюда и до конца см. вопрос №22, отрывок titkova-matmetody.pdf с. 15 от этого фрагмента и до конца отрывка)

25. t-критерий Стьюдента. Применение критерия для установления различия (сходства) средних арифметических значений в 2-х выборках.

(ответ, может быть, у Наследова на страницах 164-169)

 

с. 73 (165)

КРИТЕРИЙ Г-СТЬЮДЕНТА ДЛЯ НЕЗАВИСИМЫХ ВЫБОРОК

Метод позволяет проверить гипотезу о том, что средние значения двух ге­неральных совокупностей, из которых извлечены сравниваемые независимые выборки, отличаются друг от друга. Допущение независимости предполагает, что представители двух выборок не составляют пары коррелирующих значений признака. Это предположение нарушилось бы, если, например, 1-я выборка состояла из мужей, а 2-я — из их жен, и два ряда значений измеренного при­знака могли бы коррелировать.

Проверяемая статистическая гипотеза Н_о: М_х = М₂. При ее отклонении при­нимается альтернативная гипотеза о том, что М_х больше (меньше) М_г.

Исходные предположения для статистической проверки:

П одна выборка извлекается из одной генеральной совокупности, а другая выборка, независимая от первой, извлекается из другой генеральной со­вокупности;

□ распределение изучаемого признака и в той, и в другой выборке при­
близительно соответствует нормальному;

□ дисперсии признака в двух выборках примерно одинаковы (гомогенны).

Структура исходных данных: изучаемый признак измерен у объектов (ис­пытуемых), каждый из которых принадлежит к одной из двух сравниваемых независимых выборок.

Ограничения: распределения признака и в той, и в другой выборке суще­ственно не отличаются от нормального; в случае разной численности сравнива­емых выборок их дисперсии статистически достоверно не различаются (про­веряется по критерию F-Фишера — при вычислениях «вручную», по критерию Ливена — при вычислениях на компьютере).

Альтернатива методу: непараметрический критерий £/-Манна-Уитни — если распределение признака хотя бы в одной выборке существенно отлича­ется от нормального и (или) дисперсии различаются статистически достоверно.

Формулы для эмпирического значения критерия ^-Стьюдента:

df = N_l+N₂-2.

Формула (11.3) применяется для приближенных расчетов, для близких по численности выборок, а формула (11.4) — для точных расчетов, когда выбор­ки заметно различаются по численности.

F-критерий Фишера.

titkova-matmetody.pdf с. 67

F-критерий Фишера используется для:

1) установления сходства-различия дисперсий в двух независимых выборках (D1↔D2);

2) установления отличия от нуля коэффициента детерминации (η2 ↔"О");

3) установления наличия-отсутствия влияния фактора в дисперсионном анализе.

Случай 1

Эмпирическое значение F-критерия для сравнения двух дисперсий в независимых

выборках находят по очень простой формуле:

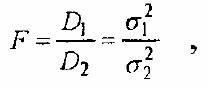
где D1 – большая дисперсия, D2 – меньшая дисперсия [Подстановка в числитель большей

дисперсии необходима для использования таблиц критических значений, в которых приводится

только правое критическое значение (больше единицы). Статистические программы рассчитывают

и левое критическое значение (меньше единицы)].

Количество степеней свободы определяется отдельно для числителя и отдельно для

знаменателя:

dfчисл= nчисл-1

dfзнам =nзнам -1

Пример 5.3.Две группы испытуемых обучались некоторым моторным навыкам по двум

разным методикам, фиксировалось количество ошибочных действий, до обучения результаты в

обеих группах имели одинаковый разброс. Какая из методик даст наибольшее выравнивание

результатов внутри группы после обучения (табл.5.3.).

Подставляя в формулу получим:

Fэмп= 36/16 = 2,25.

dfчисл= 16-1 = 15

dfзнам =21-1 = 20

Поскольку нам заранее не известно, какая из методик может обладать меньшей

дисперсией, мы используем ненаправленную гипотезу и, следовательно, двусторонний критерий.

Находим по таблице 3 (Приложение) критическое значение Fкр для α = 0,05 (α/2+α/2 = 0,05) и

dfчисл=15, dfзнам=20, Fкрит=2,573.

Получим: Fэмп=2,25∠Fкрит=2,573

Вывод: Так как эмпирическое значение меньше критического, то статистически значимых

различий дисперсий в первой и второй группах нет и, следовательно, стабилизация навыка при

обучении по обеим методикам одинакова.

Замечание. Для сравнения дисперсий в зависимых выборках более строгим будет

применение t-критерия Стьюдента.

Случай 2

В случае определения отличия от нуля коэффициента детерминации эмпирическое

значение F-критерия рассчитывается так:

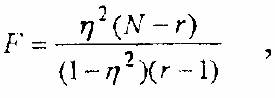
где: N – общее число испытуемых, r-число интервалов квантования, исходя из которых

рассчитывалось η2.

При определении критического значения число степеней свободы для числителя:

dfчисл=r–1,

для знаменателя:

dfзнам=N–r.

(Коэффициент детерминации – η2, определяет общую меру связи – корреляционное

отношение. Он определяется по формуле:

Здесь:

SSвнтр – сумма квадратов отклонений от внутригруппового (условного) среднего;

SSобщ – сумма квадратов отклонений от общего для всех измерений среднего (безусловного

среднего);

Следует отметить, что в отличие от линейной корреляции коэффициент детерминации

устанавливает два типа связей: зависимость х от у и зависимость у от х (η2

х/у, η2

у/х). То есть сначала

одна переменная рассматривается как зависимая, другая – как независимая, затем наоборот).

Пример 5.4.В таблице 5.4. даны результаты тестирования по двум методикам 12

испытуемых. Отличается ли коэффициент детерминации от нуля?

В нашем случае, имеем η2=0,77, N=12, r=4. Подставляя в формулу,

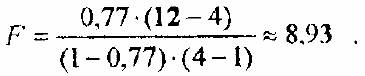
получаем Fэмп=8,93.

Критические значения F-кpитepия для α =0,05, dfчисл=4-1=3, dfзнам=12-4=8 находим по

таблице:

Fэмп=8,93>Fкр(ρ≤0,01)=7,591

Вывод: Коэффициент детерминации η2 статистически значимо отличается от нуля

(ρ<0.01).

U-критерий Манна-Уитни.

090309-matmetody.txt

Если две независимые выборки, и распределение отличается от нормального - пользуемся критерием Манна-Уитни. Непараметрический метод сравнения выборок.

с. 81 (173)

Самым популярным и наиболее чувствительным (мощным) аналогом кри­терия f-Стьюдента для независимых выборок является критерий U-Манна-Уитни (Mann-Whitney U). Непараметрическим его аналогом является критерий серий (см. главу 8), который еще проще в вычислительном отношении, но обладает заметно меньшей чувствительностью, чем критерий U.

Эмпирическое значение критерия tZ-Манна-Уитни показывает, насколько совпадают (пересекаются) два ряда значений измеренного признака. Чем мень­ше совпадение, тем больше различаются эти два ряда. Основная идея критерия Uоснована на представлении всех значений двух выборок в виде одной общей последовательности упорядоченных (ранжированных) значений. Основной (нулевой) статистической гипотезе будет соответствовать ситуация, когда зна­чения одной выборки будут равномерно распределены среди значений другой выборки, то есть когда два ряда значений пересекаются в наибольшей возмож­ной степени. Напротив, отклонению этой гипотезы будет соответствовать си­туация, когда значения одной из выборок будут преобладать на одном из кон­цов объединенного ряда — пересечение двух рядов тогда будет минимальным.

ПРИМЕР 12.1_____________________________________________________

Обозначим значения переменной для одной выборки X, а для другой выборки — У и упорядочим значения обеих выборок по возрастанию.

 

Значения

Выборка

X

X

У

X

X

X

У

X

X

У

X

У

У

Y

У

У

Значения одной выборки распределены явно не равномерно среди значений дру­гой выборки: значения выборки У преобладают на правом конце объединенного ряда. Однако критерий серий не позволяет обнаружить статистически значимые различия: всего серий в данном случае W— 8 и при т = п = $ эта величина не выхо­дит за пределы критических значений для а = 0,05 (приложение 5).

Формально, критерий U— это общее число тех случаев, в которых значе­ния одной группы превосходят значения другой группы, при попарном срав­нении значений первой и второй групп. Соответственно, вычисляются два значения критерия: U_x и U_y.

Для вычислений «вручную» используются следующие формулы: (172.JPG)

где п — объем выборки X; m — объем выборки У, R_x и R_y — суммы рангов для X и У в объединенном ряду. В качестве эмпирического значения критерия бе­рется наименьшее из U_x и U_y. Чем больше различия, тем меньше эмпирическое значение U.

Поскольку критерий U отражает степень совпадения (перекрещивания) двух рядов значений, то значениер-уровня тем меньше, чем меньше значение U. При расчетах «вручную» используют таблицы критических значений крите­рия £/-Манна-Уитни (приложение 9).

ПРИМЕР 12.1 (продолжение)

Проверим гипотезу о различии выборок X (численностью т = 8) и К (численно­стью п = 8) на уровне а = 0,05:

 

Значения

Выборка

X

X

Y

X

X

X

Y

X

X

Y

X

Y

Y

Y

Y

Y

Ранги

Ранги X

Ранги Y

5, ^9

Ш а г 5. Определяется/7-уровень значимости: наименьшее из f/сравнивается с таб­личным (приложение 9) для соответствующих объемов выборки т = 8 и п = 8. Зна­чение р < 0,05 (0,01), если вычисленное £/_энп < £/_табл В нашем случае наименьшим является U_y = 10, которое и принимается за эмпирическое значение критерия. Оно меньше критического для р = 0,05 (U= 13) , но больше критического для р = 0,01 (U=7). Следовательно,/? < 0,05.

Ш а г 6. Принимается статистическое решение и формулируется содержательный вывод. На уровне а = 0,05 принимается статистическая гипотеза о различии Xи Y по уровню выраженности признака. Уровень У статистически достоверно выше уров­ня Х(р< 0,05).

Замечание. Связи в рангах для вычислений «вручную» не предусмот­рены. Хотя они и незначительно влияют на результат, но если доля одинако­вых рангов по одной из переменных велика, то предлагаемый алгоритм не­применим, пользуйтесь компьютерной программой (SPSS, Statistica).

T-критерий Вилкоксона.

с. 84 (176)

Назначение критерия.

Критерий применяется для сопоставления показателей, измеренных в двух разных

условиях на одной и той же выборке испытуемых.

Он позволяет установить не только направленность изменений, но и их выраженность. С

его помощью мы определяем, является ли сдвиг показателей в каком-то одном направлении более

интенсивным, чем в другом.

Описание критерия Т.

Этот критерий применим в тех случаях, когда признаки измерены по крайней мере по

шкале порядка, и сдвиги между вторым и первым замерами тоже могут быть упорядочены. Для

этого они должны варьировать в достаточно широком диапазоне. В принципе, можно применять

критерий Т и в тех случаях, когда сдвиги принимают только три значения: -1, 0 и +1, но тогда

критерий Т вряд ли добавит что-нибудь новое к тем выводам, которые можно было бы получить с

помощью критерия знаков. Вот если сдвиги изменяются, скажем, от -30 до +45, тогда имеет смысл

их ранжировать и потом суммировать ранги.

Суть метода состоит в сопоставлении выраженности сдвигов в том и ином направлениях

по абсолютной величине. Для этого сначала ранжируются все абсолютные величины сдвигов, а

потом суммируются ранги. Если сдвиги в положительную и в отрицательную сторону происходят

случайно, то суммы рангов абсолютных значений их будут примерно равны. Если же

интенсивность сдвига в одном из направлений перевешивает, то сумма рангов абсолютных

значений сдвигов в противоположную сторону будет значительно ниже, чем это могло бы быть

при случайных изменениях.

Первоначально исходят из предположения о том, что типичным сдвигом будет сдвиг в

более часто встречающемся направлении, а нетипичным, или редким, сдвигом – сдвиг в более

редко встречающемся направлении.

Гипотезы.

H0: Интенсивность сдвигов в типичном направлении не превосходит интенсивности

сдвигов в нетипичном направлении.

HI: Интенсивность сдвигов в типичном направлении превышает интенсивность сдвигов в

нетипичном направлении.

Ограничения в применении критерия Т Вилкоксона

1) Минимальное количество испытуемых, прошедших измерения в двух условиях – 5 человек.

Максимальное количество испытуемых – 50 человек, что диктуется верхней границей

имеющихся таблиц. Критические значения Т приведены в Табл. VI Приложения 1.

2) Нулевые сдвиги из рассмотрения исключаются, и количество наблюдений n уменьшается на

количество этих нулевых сдвигов (McCall R., 1970, р. 36). Можно обойти это ограничение,

сформулировав гипотезы, включающие отсутствие изменений, например: "Сдвиг в сторону

увеличения значений превышает сдвиг в сторону уменьшения значений и тенденцию

сохранения их на прежнем уровне".

Пример 5.6. В выборке курсантов военного училища (юноши в возрасте от 18 до 20 лет)

измерялась способность к удержанию физического волевого усилия на динамометре. Сначала у

испытуемых измерялась максимальная мышечная сила каждой из рук, а на следующий день им

предлагалось выдерживать, на динамометре с подвижной стрелкой мышечное усилие, равное 1/2

максимальной мышечной силы данной руки. Почувствовав усталость, испытуемый должен был

сообщить об этом экспериментатору, но не прекращать опыт, преодолевая усталость и неприятные

ощущения – "бороться, пока воля не иссякнет". Опыт проводился дважды; вначале с обычной

инструкцией, а затем, после того, как испытуемый заполнял опросник самооценки волевых

качеств по методике А.Ц. Пуни (Пуни А.Ц., 1977), ему предлагалось представить себе, что он уже

добился идеала в развитии волевых качеств, и продемонстрировать соответствующее идеалу

волевое усилие. Подтвердилась ли гипотеза экспериментатора о том, что обращение к идеалу

способствует возрастанию волевого усилия? Данные представлены в табл. 5.7.

Таблица 5.7. Расчет критерия Т при сопоставлении замеров физического волевого усилия

Для подсчета этого критерия нет необходимости упорядочивать ряды значений по

нарастанию признака. Можно использовать алфавитный список испытуемых, как в данном случае.

Первый шаг в подсчете критерия Т – вычитание каждого индивидуального значения "до"

из значения "после" (можно вычитать значения "после" из значений "до", это никак не повлияет на

расчет критерия. Но лучше во всех случаях придерживаться одной системы, чтобы не запутаться

самим).

Мы видим из табл. 5.7., что 8 полученных разностей – отрицательные и лишь 3 –

положительные.

Это означает, что у 8 испытуемых длительность удержания мышечного усилия во втором

замере уменьшилась, а у 3 – увеличилась. Мы столкнулись с тем случаем, когда уже сейчас нельзя

сформулировать статистическую гипотезу, соответствующую первоначальному предположению

исследователя. Предполагалось, что обращение к идеалу будет увеличивать длительность

мышечного усилия, а экспериментальные данные свидетельствуют, что лишь в 3 случаях из 11

этот показатель действительно увеличился. Можно сформулировать лишь гипотезу,

предполагающую несущественность сдвига этого показателя в сторону снижения.

Гипотезы.

H0: Интенсивность сдвигов в сторону уменьшения длительности мышечного усилия не

превышает интенсивности сдвигов в сторону ее увеличения.

H1: Интенсивность сдвигов в сторону уменьшения длительности мышечного усилия

превышает интенсивность сдвигов в сторону ее увеличения.

На следующем шаге все сдвиги, независимо от их знака, должны быть проранжированы по

выраженности. В Таблице 5.7. в четвертом слева столбце приведены абсолютные величины

сдвигов, а в последнем столбце (справа) – ранги этих абсолютных величин. Меньшему значению

соответствует меньший ранг. При этом сумма рангов равна 66, что соответствует расчетной:

Теперь отметим те сдвиги, которые являются нетипичными, в данном случае –

положительными. В Таблице 5.7. эти сдвиги и соответствующие им ранги выделены цветом.

Сумма рангов этих «редких» сдвигов составляет эмпирическое значение критерия Т:

По таблице 4 Приложения 5.3. находим критические значения для Т-критерия Вилкоксона

для n=11:

Зона значимости в данном случае простирается влево, действительно, если бы "редких", в

данном случае положительных, сдвигов не было совсем, то и сумма их рангов равнялась бы нулю.

В данном же случае эмпирическое значение Т попадает в зону неопределенности:

Тэмп.<Ткр(0,05)

Ответ: H0 Овтвергается. Интенсивность отрицательного сдвига показателя физического

волевого усилия превышает интенсивность положительного сдвига (р<0,05).

Попытаемся графически отобразить интенсивность отрицательных и положительных

сдвигов. На Рис. 5.5. слева сдвиги представлены в секундах, а справа – в своих ранговых

значениях. Мы видим, что ранжирование несколько уменьшает площади сопоставляемых облаков,

или "фронтов".

Рисунок 5.5. Графическое представление отрицательных и положительных сдвигов; слева

в секундах, справа в ранговых значениях

Таким образом, продолжительность удержания мышечного волевого усилия во втором

замере снижается, и этот сдвиг неслучаен. Инструкция, ориентирующая испытуемого на

соответствие идеалу в развитии воли, оказалась гораздо менее мощным фактором, чем какая-то

иная сила – возможно, мышечное утомление, может быть, разочарование в себе или в

возможностях данного психологического эксперимента. А может быть, в момент второго замера

просто перестает действовать какой-то мощный фактор, который был активен вначале?

Представим выполненные действия в виде алгоритма:

АЛГОРИТМ

L-критерий Пейджа.

http://statistika.siteedit.ru/page7

L-критерий Пейджа применяется для сопоставления показателей, измеренных в трех и более условиях на одной и той же выборке испытуемых. Критерий позволяет выявить тенденции в изменении величин признака при переходе от условия к условию

l-kritery-page.htm

Критерий Пеиджа (его полное название Lкритерий тенденций Пеиджа) можно рассматривать как эквивалент критерия Фридмана для сопоставления показателей измеренных в трех и более условиях на одной и той же выборке испытуемых. Однако этот критерий не только позволяет выявить различия, но указывает на направление в изменении величин признака. Именно поэтому он является более предпочтительным.

Так, например, критерий Пеиджа позволяет проверить предположения о временной или ситуативно обусловленной динамике изменения каких-либо признаков. К сожалению, применение этого достаточно мощного критерия ограничено объемом выборки – число испытуемых не может быть больше 12 и числом измерений признака – оно не может быть больше 6.

Задача 6.6.Решим еще раз задачу 6.5, но уже помощью критерия Пеиджа, используя уже готовую таблицу 6.10. При этом основной тенденцией данного примера будем считать увеличение времени решения второго и четвертого заданий по сравнению с первым и третьим заданиями.

Решение. Подчеркнем, что первые несколько операций аналогичны операциям критерия Фридмана. Поэтому их описание мы опускаем и отсылаем к предыдущему критерию.

Дальнейшая работа с критерием Пейджа заключается в преобразовании таблицы 6.10. Следует попарно переставить столбцы таблицы 6.10, ориентируясь на величины сумм рангов так, чтобы в начале таблицы стояли столбцы с наименьшей суммой рангов, а в конце таблицы – с наибольшей. Понятно, что столбцы с соответствующими измерениями также переставляются. После проведения необходимых перестановок получается таблица 6.11.

 

 

Таблица 6.11

№ 1	№ 2	№ 3	№ 4	№ 5	№ 6	№ 7	№ 8	№ 9
№ испытуемых п/п	Время решения первого задания теста в сек.	Ранги времени решения первого задания теста	Время решения третьего задания теста в сек.	Ранги времени решения третьего задания теста	Время решения четвертого задания теста в сек.	Ранги времени решения четвертого задания теста	Время решения второго задания теста в сек.	Ранги времени решения второго задания теста
				2,5				2,5
Сумма рангов				11,5				19,5

Теперь все готово для подсчета эмпирического значения L_эмп критерия Пейджа. Оно определяется по формуле:

где R_i – сумма рангов i-того столбца в упорядоченнойтаблице

i– порядковый номер столбца, получившийся в новойтаблице, упорядоченной по сумме рангов

с – число измерений.

Используя формулу (6.2) вычисляем эмпирическое значение L_эмп для нашего примера:

По таблице 5 Приложения определяем критические значения L_крдля числа испытуемых n = 6 и для числа измерений с = 4. Отметим, что в таблице критических значений критерия Пейджа добавлен уровень значимости 0,001 или 0,1%. Представим соответствующий блок таблицы 5 Приложения в виде таблицы 6.12.

Таблица 6.12

№ – число испытуемых	С – количество измерений 4	Р – уровень значимости Р
		0,001
		0,01
		0,05

Используя привычную форму записи для критических величин, получаем следующее выражение:

Строим “ось значимости”:

В нашем примере значение L_эмппопало в зону неопределенности, следовательно, можно считать, что тенденция увеличения времени решения заданий теста №№ 2 и 4 по сравнению с заданиями №№ 1 и 3 оказалась значимой на уровне 5 %.

Переформулируем полученный результат в терминах нулевой и альтернативной гипотез: поскольку между показателями, измеренными при решении четырех заданий теста, существуют не случайные различия на 5 % уровне значимости, то нулевая гипотеза Н₀, т.е. гипотеза о сходстве отвергается, и принимается альтернативная гипотеза Н₁ о наличии различий.

Сравнивая выводы, полученные при решении задачи 5 с помощью критериев Фридмана и Пейджа, можно подумать, что они не согласуются друг с другом. Однако это не совсем так. Эти критерии обращаются к разным сторонам анализируемого материала, характеризуя различные аспекты обрабатываемых данных. Если первый критерий – Фридмана – выявляет наличие различий в измеренных показателях (признаках), то критерий Пейджа позволяет выявить тенденцию в изменениях величин измеряемых признаков.

Приведем еще один пример использования критерия Пейджа.

Задача 6.7.Психолог высказывает предположение о наличии следующей тенденции: время решения заданий теста будет возрастать по мере увеличения их сложности.

Решение. Для выявления этой тенденции психолог сравнивает время решения пяти заданий теста у тех же шести испытуемых. Поскольку начальные операции с данными представлены выше, то результаты обработки по критерию Пейджа сразу представим в виде таблицы 6.13.

Как всегда необходимо проверить правильность ранжирования. Общая сумма рангов составила: 11 + 22 + 11,5 + 19 + 26,5 = 90

Согласно формуле (1.3): n ´ c ´ (c + 1) : 2 она должна быть 6 ´ 5 ´ (5 + 1) : 2 = 90

Таблица 6.13

№ испытуемых п/п	Время решения первого задания теста в сек.	Ранги времени решения первого заданиятеста	Время решения второго задания теста в сек.	Ранги времени решения второго задания теста	Время решения третьего задания теста в сек.	Ранги времени решения третьего заданиятеста	Время решения четвертого задания тестав сек.	Ранги времени решения четвертого заданиятеста	Время решения пятого задания в сек.	Ранги времени решения пятого задания теста
				2,5		2,5
				4,5						4,5
Сумма рангов						11,5				26,5

Сравнив результаты первого и второго подсчета рангов, делаем вывод о том, что ранжирование произведено правильно.

Теперь, чтобы подсчитать L_эмппо формуле (6.2), не будем строить новую таблицу, а применим второй способ вычислений. Для этого рассмотрим сумму рангов как обычный ряд чисел и проранжируем этот ряд. Причем каждой величине этого нового, упорядоченного ряда поставим в соответствие его ранг. Этот ранг в формуле (6.2) обозначен как индекс i. Поэтому получатся следующие соответствия:

Теперь, имея суммы рангов и соответствующие им индексы, можно применить формулу (6.2):

Следующим этапом, как всегда, является нахождение критических величин для соответствующего числа испытуемых и измерений.

По таблице 5 Приложения находим для n = 6 и с – 5:

Строим соответственно “ось значимости”:

Полученная величина L_эмпкритерия тенденций Пейджа оказалась значимой на 0,1% уровне. Следовательно, по мере увеличения сложности заданий, увеличивается и время их решения.

В терминах статистических гипотез полученный результат таков: Н₀ – нулевая гипотеза о сходстве должна быть отвергнута, а на уровне 0,1% следует принять альтернативную гипотезу Н₁ о наличии различий. Иными словами, тенденция увеличения времени решения заданий теста с увеличением их сложности не является случайной.

Для применения критерия Пейджа необходимо соблюдать следующие условия:

1. Измерение может быть проведено в ранговой, интервальной ив шкале отношений.

2. Выборка должна быть связной.

3. В выборке должно быть не менее двух и не больше 12 испытуемых, каждый из которых имеет не менее трех измеренных показателей.

4. Применение критерия ограничено, так как таблицы критических значений рассчитаны на небольшую выборку (n < 12) ималенькое число измерений (не больше 6). Если эти ограничения не выполняются, приходится использовать критерийФридмана.

 

 

31. χ2-критерий Пирсона. Применение критерия для установления сходства-различия между эмпирическим и равномерным распределением.

с. 31 (123) 121.JPG

 

Глава 9

АНАЛИЗ НОМИНАТИВНЫХ ДАННЫХ

Методы, о которых пойдет речь в этой главе, касаются проверки, по-види­мому, самого широкого класса гипотез — в отношении тех явлений, измере­ния которых доступны в номинативной шкале.

ПРИМЕРЫ

Кто чаще обращается в службу знакомств: мужчины или женщины? Зависит ли количество аварий на производстве от дня недели? Можно ли утверждать, что водители-женщины чаще становятся участниками ДТП (дорожно-транспортных происшествий)?

Можно ли утверждать, что выигрыши в игре распределены не случайно среди про­игрышей?

Данные для ответов на подобные обыденные и чисто академические вопросы могут быть получены при помощи простого способа — классификации событий и людей по интересующим градациям. И несмотря на, казалось бы, бесчисленное многообразие подобных ситуаций, все они могут быть сведены /с трем типичным случаям:

1 — сравнение наблюдаемого (эмпирического) распределения частот с ожи­
даемым (теоретическим) распределением;

2 —- сравнение двух или более наблюдаемых распределений частот;

3 — сравнение наблюдаемого распределения событий X среди событий Y
(серий X, Y) со случайным распределением.

ПРИМЕРЫ___________________________________________________

Случай I.

1. Кто чаще обращается в службу знакомств: мужчины или женщины? Для ответа
на этот вопрос необходимо: а) подсчитать количество женщин и мужчин, обра­
тившихся в службу знакомств; б) воспользовавшись методом статистической
проверки, сопоставить полученное эмпирическое соотношение мужчин и жен­
щин с ожидаемым (теоретическим) равномерным распределением.

Зависит ли количество аварий на производстве от дня недели? Проверка этого
предположения требует выполнения сходных действий: а) подсчитать количе­
ство аварий для каждогодня недели за достаточно длительный промежуток времени; б) воспользовавшись методом статистической проверки, сопоставить по­лученное эмпирическое распределение количества аварий по дням недели с ожи­даемым (теоретическим) равномерным распределением.

Случай П.

1. Зависит ли предпочтение напитка (минеральная вода, сок, лимонад) от сезона
(зима, весна, лето, осень)? Для проверки этого предположения необходимо для
каждого респондента определить тип предпочитае­
мого напитка (первая номинативная переменная, 3

градации) и сезон опроса (вторая номинативная пе­ременная — 4 градации).

2. Зависит ли предпочтение одного из пяти кандида­
тов на выборах от пола потенциального избирате­
ля? Для проверки этого предположения необходи­
мо для каждого респондента определить пол (первая
номинативная переменная, 2 градации) и предпо­
читаемого кандидата, одного из пяти (вторая номи­
нативная переменная, 5 градаций).

3. Повлияла ли рекламная кампания на выбор респондентами одного из двух
товаров? Это предположение требует опроса респондентов на предмет предпоч­
тения одного из двух товаров дважды: до рекламной кампании (первая номина­
тивная переменная, две градации) и после нее (вторая номинативная перемен­
ная, те же две градации).

Для решения подобных задач, связанных с анализом классификаций или таблиц сопряженности, оказывается достаточным применение одного и того же критерия — у}-Пирсона:

(9.1)

где Р— количество ячеек таблицы распределения или сопряженности, содер­жащих эмпирические значения частот;/,,/. — эмпирическое и теоретическое значения частот для одной ячейки; к— число градаций сопоставляемых рас­пределений; / — количество сопоставляемых распределений. Приведенная формула является общей для различных ситуаций, и в каждом случае ее при­менение обладает своей спецификой.

ПРИМЕРЫ

Случай III.

!. Является ли закономерным последо<