Гистограмма – это столбиковая диаграмма, в которой каждый столбик обозначает вероятность попадания значения случайной величины в определенный интервал. Гистограммы, как и контрольные карты используются для экспресс-контроля состояния технологического процесса (проверке гипотезы о нормальном распределении его результатов).
Считается, что для объективного вида гистограммы при ее построении требуется не менее 50 значений ( 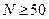 ). Воспользуемся для этих целей данными, приведенными в табл. 4.5. Методика построения гистограммы включает следующие шаги:
). Воспользуемся для этих целей данными, приведенными в табл. 4.5. Методика построения гистограммы включает следующие шаги:
1. Количество столбцов определяется по формуле:  . Как правило, наиболее удобным является нечетное количество столбцов, тогда центральный становится осью симметрии. В нашем случае N=90 и мы примем C=9.
. Как правило, наиболее удобным является нечетное количество столбцов, тогда центральный становится осью симметрии. В нашем случае N=90 и мы примем C=9.
2. Рассчитывается размах R = xmax-xmin , (разность максимального и минимального значений в выборке). R = 2,545 – 2,502 = 0,043.
3. Определяется длина интервала K = R/C. Значение K часто получается дробным и требует округления. Количество знаков после запятой выбирается с учетом двух критериев: возможности использовать для построения все имеющиеся значения (последний интервал должен включить максимальное значение) удобства использования гистограммы (читаемость, непротиворечивость). В нашем случае K = R/C = 0,043/9 = =0,004778. Если мы проведем округление в меньшую сторону до 0,004, то максимальное значение2,545 не будет входить в последний, 9-й интервал. Поэтому примем K=0,005.
4. Длину интервала K прибавим к xmin иполучим верхнюю границу первого интервала (2,502+0,005 = 2,507). Полученное значение будет являться нижней границей второго интервала, к нему мы также добавим длину интервала и т. д. Полученные интервалы занесем в специальный контрольный листок, табл. 4.6
5. Далее подсчитывается количество значений, относящихся к каждому интервалу. Для этого в соответствующие строки контрольного листка заносятся штриховые отметки. Что делать, если исходное значение равно граничному, например, 2,507? В этом случае оно относится к тому интервалу, где является НИЖНЕЙ границей. Исключение может составить только максимальное значение в последнем интервале.
6. После проведения контроля за счет подсчета накопленной частоты, и определяется вероятность попадания значения в каждый из интервалов i:  , где Pi – вероятность попадания значения в i-й интервал Ni – количество значений выборки, входящих в i-интервал
, где Pi – вероятность попадания значения в i-й интервал Ni – количество значений выборки, входящих в i-интервал
7. По полученным данным строим гистограмму, рис. 4.6. На ней может отмечаться количество вхождений, вероятность или и то и другое.
Таблица 4.6.
Контрольный листок для построения гистограммы
| Интервалы | Штриховые отметки частоты | Частота | Накопленная частота | Вероятность |
| 2,502-2,507 | // | 0,022 | ||
| 2,507-2,512 | ////\ | 0,056 | ||
| 2,512-2,517 | ////\ // | 0,078 | ||
| 2,517-2,522 | ////\ ////\ ////\ // | 0,189 | ||
| 2,522-2,527 | ////\ ////\ ////\ ////\ //// | 0,256 | ||
| 2,527-2,532 | ////\ ////\ ////\ / | 0,178 | ||
| 2,532-2,537 | ////\ ////\ / | 0,122 | ||
| 2,537-2,542 | //// | 0,044 | ||
| 2,542-2,547 | ////\ | 0,056 |

Рис. 4.6. Пример гистограммы
Анализ техпроцесса с помощью гистограммы построен на сравнении ее формы с кривой нормального распределения (см. п. 3.1 пособия). Если мы отметим на гистограмме граничные значения Tн и Tв, сразу появится картина управляемости процесса. В нашем случае крайние столбцы (1-й и 9-й) находятся очень близко к границам распределения.
Диаграммы рассеивания
Диаграмма рассеивания (диаграмма разброса) – это точечная диаграмма - множество точек – где форма множества свидетельствует о взаимосвязи между парами соответствующих переменных. Мы уже рассматривали выше (п. 3.3) определение коэффициента корреляции как один из способов сделать это. Однако, построение диаграммы рассеивания – более простой способ. Рассмотрим три основных вида диаграммы разброса на рис. 4.7.

Рис. 4.7 Примеры диаграмм разброса:
а) – положительная корреляция
б) – отрицательная корреляция
в) – корреляция отсутствует
Как мы помним, наличие положительной корреляции между случайными величинами означает прямую связь между ними, т.е. с ростом одной величины растет и другая. Отрицательная корреляция (рис. 4.7, б) означает, что с ростом одной из величин вторая уменьшается. Наконец, отсутствие корреляции – отсутствие какого-либо влияния роста одной из величин на другую.
Рассмотрим пример из п. 3.3 нашего пособия. Данные за неделю:
| Относ. вл-ть воздуха, % | |||||||
| Доля дефектов, % | 2,2 | 2,6 | 2,1 | 2,7 | 2,8 | 2,6 | 2,2 |
Используем эти данные, чтобы построить диаграмму рассеивания. Используем каждую пару значений как координаты одной точки. Результаты представлены на рис. 4.8. Как видно, точки выстраиваются в упорядоченное облако, соответствующее положительной корреляции.

Рис. 4.8. Диаграмма рассеивания с положительной корреляцией
Как мы помним, значение коэффициента корреляции рассчитанное в п. 3.3 составляло 0,95. Однако, строить диаграмму рассевания значительно проще.
Блок-схемы
Блок-схемой называется нотация (графические символы и правила их построения), позволяющая наглядно отразить алгоритм процесса в организации. Основные символы представлены на рис. 4.9.

Рис. 4.9. Основные символы, используемые в блок-схемах (Flowchart)
Рассмотрим на рис. 4.10, как будет выглядеть алгоритм цикла Шухарта-Деминга PDCA в виде блок-схемы.
Основное применение блок-схемы получают при стандартизации процессов, которую мы рассмотрим в гл. 5 и 6. Как правило, при решении задач управления качеством блок-схема строится в организационном разрезе, т. е. символы соответствуют подразделению, где выполняются действия и принимаются решения. В этом случае невозможна двойственная и неоднозначная ответственность за операции процессов. Пример блок-схемы в организационном разрезе приведен на рис. 4.11. Помимо нотации Flowchart для описания процессов используются нотации IDEF0, IDEF3, DFD.

Рис. 4.10. Блок-схема цикла Шухарта-Деминга PDCA

Рис. 4.11. Пример построения блок-схемы в организационном разрезе
Методические указания:
· изучить дополнительные материалы:
Ø Гиссин В. И. Управление качеством (2-е издание). – Москва: ИКЦ «МарТ», Ростов-н/Д: Издательский центр «МарТ», 2003. – Гл. 3,
с. 165-223.
Ø Статистические методы повышения качества: Пер. с англ./Под ред. Х.Кумэ. – М.: Финансы и статистика, 1990. – гл.2, с.24-36, гл.3,
с.36-44, гл.4, с.44-57, гл.7, с.57-87,112-170.
Ø Андерсен Б. Бизнес-процессы. Инструменты совершенствования / Пер. с англ. С.В. Ариничева. – М.: РИА "Стандарты и качество", 2003.
Выполнить практические задания из раздела 4 практикума.
Глава 5. Стандартизация
5.1. Понятие и история стандартизации.
5.2. Научно-технические принципы стандартизации.
5.3. Категории и виды стандартов.
5.4. Основы государственной системы стандартизации.
5.5. Работы, выполняемые при стандартизации.
Дата: 2016-09-30, просмотров: 348.