| Принято решение Значение контролируемого параметра | «Годен» | «Брак» |
| В допускаемых пределах, «годен» | Нормальная ситуация | Ошибка первого рода |
| Вне пределов допускаемых значений, «брак» | Ошибка второго рода | Нормальная ситуация |
Вероятность ошибки первого рода, т.е. ситуации, при которой годная продукция ошибочно забракована, называют риском поставщика и обозначают a .
Вероятность ошибки второго родат.е. ситуации, при которой бракованная продукция ошибочно принята, называют риском потребителя и обозначают b .
Пусть D – число дефектных изделий в партии объемом N изделий, тогда q=D/N – доля дефектных изделий.
В практике статистического контроля генеральная доля q неизвестна и ее следует оценить по результатам контроля случайной выборки объемом n изделий, из которых m дефектных.
Под планом статистического контроля понимают систему правил, указывающих методы отбора изделий для проверки, и условия, при которых партию следует принять, забраковать или продолжить контроль.
Различают следующие виды планов статистического контроля партии продукции по альтернативному признаку:
- одноступенчатые планы, согласно которым, если среди n случайно отобранных изделий число дефектных m окажется не больше приемочного числа С (m  C), то партия принимается; в противном случае партия бракуется;
C), то партия принимается; в противном случае партия бракуется;
- двухступенчатые планы, согласно которым, если среди n1 случайно отобранных изделий число дефектных m1 окажется не больше приемочного числа C1 (m1  C1), то партия принимается; если m1
C1), то партия принимается; если m1  1, где d1 – браковочное число, то партия бракуется. Если же C1 < m1 < d1, то принимается решение о взятии второй выборки объемом n2. Тогда, если суммарное число изделий в двух выборках (m1 + m2)
1, где d1 – браковочное число, то партия бракуется. Если же C1 < m1 < d1, то принимается решение о взятии второй выборки объемом n2. Тогда, если суммарное число изделий в двух выборках (m1 + m2)  C2, то партия принимается, в противном случае партия бракуется по данным двух выборок;
C2, то партия принимается, в противном случае партия бракуется по данным двух выборок;
- многоступенчатые планы.
Оперативной характеристикой плана контроля называется функция P(q), равная вероятности принять партию продукции с долей дефектных изделий q=D/N, где D-число дефектных изделий в партии из N изделий.
В идеальном случае есть граничная доля q0 и
 , т. е. (3.10)
, т. е. (3.10)
партия принимается, если доля дефектов ниже граничной, либо бракуется, если доля дефектов выше.
Но на практике, поскольку контролю подвергается выборка (часть партии), а не партия целиком, то всегда существует вероятность совершить ошибку как первого так и второго рода. Поэтому определяют q0 – приемлемый уровень качества и qm – браковочный уровень качества и
 ; (3.11)
; (3.11)
 .
.
Например, известны значения q0 = 0,005; qm = 0,02; a=0,02; b=0,05. Тогда можно прочитать характеристику статистического плана приемочного контроля следующим образом: «Из каждых 100 партий с долей бракованных изделий 0,5% будет ошибочно забраковано не более 2 (партий), а из каждых 100 партий с долей бракованных изделий 2% будет ошибочно принято не более 5».
Значение оперативной характеристики плана контроля P(q) рассчитывается по формуле:
 , (3.12)
, (3.12)
где Pn(m) – вероятность того, что в выборке объемом n обнаружится m дефектных изделий.
Формула означает, что вероятность принять партию равна сумме вероятностей: того, что в выборке не будет обнаружено ни одного дефектного изделия, того, что будет обнаружено одно, и так далее до вероятности обнаружить c дефектных изделий.
Рассчитать значения Pn(m) возможно наиболее точным, но в то же время и наиболее трудоемким способом, исходя из гипотезы о гипергеометрическом распределении бракованных деталей в партии. Тогда:
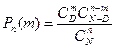 , где (3.13)
, где (3.13)
 - количество сочетаний из N по М, которое определяется как
- количество сочетаний из N по М, которое определяется как
 . (3.14)
. (3.14)
N! = 1*2*3…*N; 0! = 1. 

Если объем выборки n не превышает 10% объема партии (n≤0,1N), то вычисления можно упростить, используя гипотезу о биномиальном распределении бракованных деталей в партии:
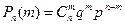 , где (3.15)
, где (3.15)
p=1 – q.
Использование гипотезы о биномиальном распределении позволяет провести вычисления наиболее быстро, если недоступны вычислительные средства, кроме микрокалькулятора.
Если n≤0,1N и q<0,1, то вычисления можно еще более упростить (если есть возможность использовать компьютер или расчетные таблицы), используя гипотезу о распределении Пуассона:
 , где (3.16)
, где (3.16)
l = nq
После вычислений значения оперативной характеристики плана контроля, рассчитывают значения риска поставщика a и риска производителя b.

Рис. 3.4. Семейство оперативных характеристик планов контроля
Для достижения оптимальных значений a и b изменяют значения c и n. Увеличение выборочного числа приводит к уменьшению риска производителя, увеличение объема выборки – к уменьшению риска потребителя. Изменения оперативных характеристик удобно иллюстрировать графически, как показано на рис. 3.4.
Рассмотрим пример. Точка розничной продажи регулярно принимает от поставщиков партии из 50 сменных фильтров для воды. В связи с тем, что в последнее время начали поступать жалобы на фильтры, принято решение разработать план статистического контроля для предотвращения ситуации в дальнейшем. Поставщик предложил следующий одноступенчатый план:
Из партии объемом 50 фильтров (N=50) контролируется 1 фильтр (n=1),который должен оказаться годным (с = 0). Приемочный уровень дефектности составляет 4% (q0=0,04), браковочный уровень – 20% (qm=0,2).
Чтобы сделать вывод о выгодности такого плана, необходимо построить оперативную характеристику плана контроля.
Решение.
Определим значение оперативной характеристики для двух точек: q0 и qm, пользуясь гипотезой о гипергеометрическом распределении дефектов в партии.
1) q=q0.
q=D/N; 0,04=D/50; D=0,04*50 = 2.
Т.е. для 4%-го уровня засоренности дефектами в партии должно быть 2 дефектных изделия.
 ;
; 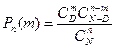

P(q0)=0,96.
Отметим, что для расчета P(q) мы использовали только одно слагаемое Pn(m) для m=0. Дело в том, что нас интересует только одна ситуация: в выборке нет дефектных изделий. Если бы в условии мы имели c=1, нас устроили бы две ситуации: в выборке нет дефектов или есть одно дефектное изделие, и мы рассчитывали бы P(q) как сумму двух слагаемых: для m=0 и m=1.
Вычисления оказались простыми, поскольку факториалы можно сокращать. Если 5!=3!*4*5, то 48!=47!*48 (и мы сократили дробь на 47!), а 50!=49!*50, и мы сократили дробь на 49!
2) q=qm.
q=D/N; 0,2=D/50; D=0,2*50 = 10.


P(qm)=0,8.
3) Зная значения P(q0) и P(qm), мы можем определитьриски поставщика и производителя:
 ; P(q0) = 1- a; 0,96 = 1 - a; a = 0,04.
; P(q0) = 1- a; 0,96 = 1 - a; a = 0,04.
 ; P(qm) = b; b=0,8.
; P(qm) = b; b=0,8.
Видно, что риск потребителя в 20 раз выше риска поставщика, т. е. предлагаемый план статистического контроля не является взаимовыгодным. Неравенство рисков можно также оценить по графику на рис. 3.5. Для снижения вероятности ошибки второго рода при заданных q0 и qm необходимо увеличить объем выборки n.

Рис. 3.5. Оперативная характеристика плана контроля для расчетного примера
Дата: 2016-09-30, просмотров: 362.