Как мы уже отмечали, рассматривая принцип менеджмента качества «Принятие решений на основе фактов», управлять качеством невозможно, не развивая т. н. «статистическое мышление». Необходимо всегда оценивать не конкретные величины и показатели, а закон, который ими управляет. В связи с этим вспомним основные постулаты статистики.
В результате сбора численных данных получается статистическая выборка. Важными свойствами стат. выборки являются: математическое ожидание, размах, дисперсия (квадрат отклонения), среднее квадратическое отклонение. Эти свойства ранее были изучены в рамках дисциплин «Теория статистики» и «Математическая статистика». Закон, по которому распределяются значения в выборке, называется распределением случайной величины.
Существуют различные виды распределения случайных величин: нормальное, биноминальное, распределение Пуассона. Очень часто нормальное распределение используется как модель, т. к. многие совокупности измерений имеют распределение, приближающееся к нормальному.
Математические закон нормального распределения можно представить следующим образом:
 , где (3.1)
, где (3.1)
m – математическое ожидание;
d – среднеквадратическое отклонение.
При всей видимой сложности формулы нормальное распределение характеризуется только двумя параметрами: математическим ожиданием и средним квадратическим отклонением, которые рассчитываются по формулам:
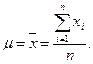 (3.2)
(3.2)
 , (3.3)
, (3.3)
 (3.4)
(3.4)
Значение под корнем в формуле называют дисперсией и обозначают d2.
Нормальное распределение можно узнать по колоколообразной форме либо при более подробном описании: а) его наибольшая частота приходится на середину интервала и плавно спадает к концам, б) оно симметрично, что можно увидеть на рис. 3.1.

Рис. 3.1. Кривые нормального распределения (f(x) – вероятность)
Значение под знаком квадратного корня – дисперсия выборки. Как видно из рис. 3.1, с увеличением дисперсии значения выборки сильнее отклоняются от средней величины (мат. ожидания). Т.о., увеличение d приводит к «сплющиванию» кривой. Увеличение m приводит к сдвигу кривой вправо (уменьшение - влево)
Нормальное распределение возникает, когда данная случайная величина представляет собой сумму большого числа независимых случайных величин, что как раз имеет место управлении качеством.
Обычная задача в управлении качеством, связанная со статистическими выборками, заключается в следующем. Необходимо достичь такого состояния технологического процесса, при котором обеспечивается производство продукции со значением одного из параметров, равным заданной величине Хн. Т. е. необходимо

Поскольку технологический процесс всегда будет предусматривать разброс значений, задаются границы допуска Tв (верхняя) и Tн (нижняя), причем любое значение x контролируемого параметра должно находиться в их пределах
Тв ³ x ³ Тн.
Например, может стоять задача производства кусков мела с длиной каждого куска 130 мм. ±5 мм. Тогда Хн = 130; Тн=125; Тв=135.
Вместо Tв и Tн используются также обозначения:
ВГД (верхняя граница допуска) = UCL (upper control level) = Tв;
НГД (верхняя граница допуска) = LCL (low control level) = Tн.
Для контроля состояния производственного процесса вычисляют ряд показателей. Коэффициент точности технологического процесса КТ равен:
 где (3.5)
где (3.5)
T =D= Tв – Tн - диапазон допустимых значений.
По полученному значению Кт судят об управляемости техпроцесса, что наглядно отражено на рис. 3.2:
если КТ <= 0,75, то технологический процесс протекает нормально;
если 0,75 < КТ <= 0,98, то требуется наладка оборудования;
если КТ > 0,98, то технологический процесс вышел из-под контроля.

Рис. 3.2. Вид кривой нормального распределения при различных значениях КТ
В продолжение нашего примера:
Рассмотрим пример расчета Кт.
Имеется следующая выборка по результатам технологического процесса: 126; 130; 126; 134; 134. На практике в выборки – в целях точности – включают не менее 50 значений, но в данном случае мы умышленно берем маленькую выборку для простоты вычислений.




T=Тв-Тн= 135-125=10.

Сверим полученное значение Кт с эталонными. Получаем, что поскольку Кт> 0,98, то процесс вышел из-под контроля.
Обратим внимание, что ни одно из значений выборки (см. условие) не выходило за границы допуска. На первый взгляд, процесс кажется хоть и не идеальным, но вполне управляемым. Но на самом деле, гипотеза о нормальном распределении результатов техпроцесса подсказывает, что если значения, с которыми мы столкнулись, находятся на границах допуска, то есть и те значения, которые выходят за границы допуска. Поэтому вывод закономерен.
В практике управления качеством вместо показателя КТ используется также показатель Ср, т. н. индекс воспроизводимости процесса.
 (3.6)
(3.6)
Общепринятые оценки процесса по индексу Ср:
Cp < 1 – «неудовлетворительно»;
1 < Cp < 1,33 – «удовлетворительно»;
Cp > 1,33 – «хорошо».
Однако, для полной картины управляемости технологического процесса оказывается недостаточным рассчитать коэффициент точности или индекс воспроизводимости. Дело в том, что при даже небольшом разбросе значений может возникнуть сдвиг кривой нормального распределения за границы допуска, что показано на рис. 3.3.

Рис. 3.3 Смещение кривой нормального распределения
В связи с такой возможностью рассчитывают т. н. откорректированный индекс Срк,
 , где (3.7)
, где (3.7)
 (3.8)
(3.8)
Или
 . (3.9)
. (3.9)
В продолжение нашего примера рассмотрим пример расчета Кт
Имеется следующая выборка результатов технологического процесса: 126; 124; 126; 127; 127.





Сверив полученное значение Кт с эталонными, получаем, что технологический процесс находится в удовлетворительном состоянии.
Однако, среди значений выборки мы можем видеть x2=124, которое выходит за нижнюю границу допуска. Значит, наш вывод ошибочен.
Рассчитаем откорректированный индекс воспроизводимости технологического процесса Срк



Как видим, значение Срк < 1, т. е. технологический процесс находится в неудовлетворительном состоянии.
На практике необходимость расчета откорректированного индекса Срк становится очевидной, как только рассчитывается среднее значение выборки, m, которое оказывается приближенным к одной из границ допуска.
Передовые в области качества предприятия уже более 20 лет назад решили, что точность технологического процесса, равная 3s (расстояние от центра распределения до границы допуска), их не устраивает как недостаточная. В компании «Моторола» в 1979 г. определили, что их некачественная продукция обходится слишком дорого, и разработали концепцию «6 сигма». В ее основе лежит уже известный нам цикл Шухарта-Деминга, и многоуровневая система обучения, схожая с обучением боевым искусствам (с высшим уровнем – черным поясом). В табл. 3.1. показано, каким образом можно соотнести рассмотренный нами уровень точности «3 сигма», для которого мы рассчитывали индексы воспроизводимости, и уровень «6 сигма».
Таблица 3.1.
Дата: 2016-09-30, просмотров: 339.