Пример 1. Решить неравенство: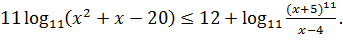 
В заданиях 15 ЕГЭ по математике (профиль) часто встречаются логарифмические неравенства. Решение логарифмических неравенств начинается с определения области допустимых значений. В данном случае в основании обоих логарифмов нет переменной, есть только число 11, что существенно упрощает задачу. Поэтому единственное ограничение, которое у нас здесь есть, заключается в том, что оба выражения, стоящие под знаком логарифма, положительны:
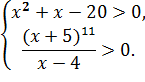
Первое неравенство в системе — это квадратное неравенство. Чтобы его решить, нам бы очень не помешало разложить левую часть на множители.
Раскладываем на множители следующим образом:
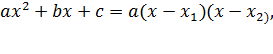
где x 1 и x 2 — корни уравнения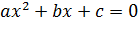 
. В данном случае коэффициент 
равен 1 (это числовой коэффициент, стоящий перед x 2). Коэффициент b тоже равен 1, а коэффициент c — это свободный член, он равен -20. Корни трёхчлена проще всего определить по теореме Виета. Уравнение у нас приведённое, значит сумма корней x 1 и x 2 будет равна коэффициенту b с противоположным знаком, то есть -1, а произведение этих корней будет равно коэффициенту c, то есть -20. Легко догадаться, что корни будут -5 и 4.
Теперь левую часть неравенства можно разложить на множители:
.
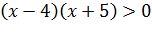Решаем это неравенство. График соответствующей функции — это парабола, ветви которой направлены вверх. Эта парабола пересекает ось X в точках -5 и 4. Значит, искомое решение неравенства — это промежуток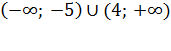 
. То есть записанное выше множество — это и есть область допустимых значений неравенства.
Итак, с учётом разложения на множители, исходное неравенство принимает вид:
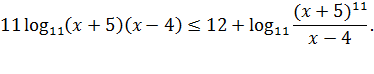
Используя формулу 
внесём 11 в степень выражения, стоящего под знаком первого логарифма, и перенесём второй логарифм в левую сторону неравенства, изменив при этом его знак на противоположный:
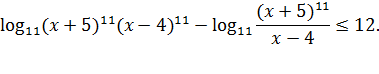
После сокращения получаем: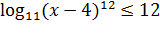 
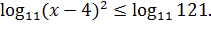
Последнее неравенство, в силу возрастания функции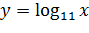 
, эквивалентно неравенству 
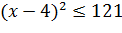, решением которого является промежуток 
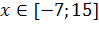. Осталось пересечь его с областью допустимых значений неравенства, и это получится ответ ко всему заданию.
Итак, искомый ответ к заданию имеет вид: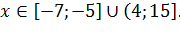 
Пример 2. Решите неравенство:
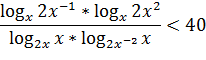
Решение.
Решение начинаем с определения области допустимых значений данного неравенства. В основании каждого логарифма должно находиться положительное число, которое не равно 1. Все выражения, стоящие под знаком логарифма должны быть положительны. В знаменателе дроби не должно оказаться нуля. Последнее условие эквивалентно тому, что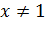 
, поскольку лишь в противном случае оба логарифма в знаменателе обращаются в нуль. Все эти условия определяют область допустимых значений этого неравенства, задающуюся следующей системой неравенств:
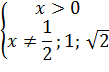
В области допустимых значений мы можем использовать формулы преобразования логарифмов для того, чтобы упростить левую часть неравенства. С помощью формулы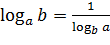 
избавляемся от знаменателя:
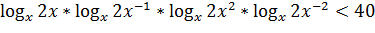
Теперь у нас получились только логарифмы с основанием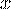 
. Это уже удобнее. Далее используем формулу 
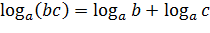, в также формулу 
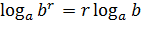для того, чтобы привести выражение, стоящее слева, к следующему виду:
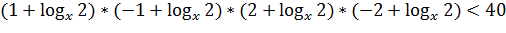
При вычислениях мы использовали то, что в области допустимых значений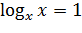 
. Используя замену 
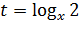, приходим к выражению:
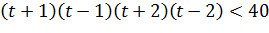
Далее используем формулу «разность квадратов», чтобы преобразовать неравенство к следующему виду:
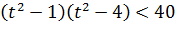
Используем ещё одну замену: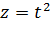 
. В результате чего приходим к следующему результату:
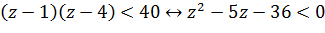
Это квадратное неравенство решается стандартным образом. В ответе получается промежуток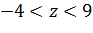 
.
Итак, постепенно возвращаемся к исходным переменным. Сперва к переменной t:
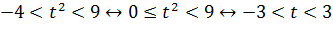
Далее возвращаемся к переменной x:
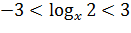
В области допустимых значений последнее двойное неравенство можно представить в виде:
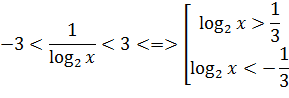
Последняя совокупность равносильна следующей:
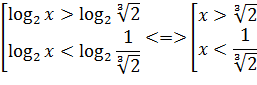
Это уже почти ответ. Осталось только пересечь его с областью допустимых значений. Для этого расположим все ключевые точки в порядке возрастания: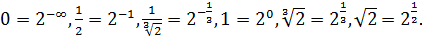 
Тогда несложно определить, что окончательный ответ будет иметь вид:
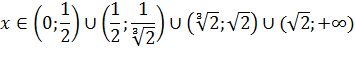
Заключение
В данной работе была кратко приведена основная теоретическая информация, необходимая для решения уравнений, неравенств и систем. Помимо этого, были рассмотрены некоторые общие приемы решения таких уравнений, неравенств и систем, и приведены примеры решения. Следует отметить, что эти примеры часто вызывают затруднения у школьников при подготовке к Единому государственному экзамену по математике. Это, в свою очередь, требует повышенного внимания к данной теме.
Уравнения, неравенства и системы встречаются учащимся, как при решений заданий частиB, так и при решении заданий уровня повышенной сложности, встречающихся в части С. В последнем случае, задания требуют от учащихся уверенных навыков решения, и наиболее рационально подходить к решению этих заданий в рамках функционального метода решения уравнений, неравенств и систем.
Список используемой литературы
1. В. А. Гусев, А. Г. Мордкович «Математика. Справочные материалы», Книга для учащихся, М.: «Просвещение», 1990 г.2. Л.О.Денищев, Е. М.Бойченко и др. «Готовимся к единому государственному экзамену», Математика, Изд. «Дрофа», 2004 г.3. Ф. Ф.Лысенко, В. Ю.Калашников «Подготовка к ЕГЭ поматематике», Ростов-на-Дону, 2002 г.
4. Азаров А.И., Барвенов С.А., Федосенко В.С., Шибут А.С. Системы алгебраических уравнений. Текстовые задачи. Справочное пособие для абитуриентов и школьников. 1998. - 288 с.
5. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 11 класса. Учеб. пособие для учащихся шк. и классов с углубл. изуч. математики. 4-е изд. - М.: Просвещение, 1995. - 335 с.
6. Галицкий М.Л., Гольдман А.М., Звавич Л.И. Сборник задач по алгебре для 8-9 классов. Учеб. пособие для учащихся шк. и классов с углубл. изуч. курса математики. М.: Просвещение, 1992. - 271 с.
7. Самусенко А.В., Казаченок В.В. Математика: Типичные ошибки абитуриентов. 2-е изд., испр. - Мн.: Выш. шк., 1995.- 185 с.
8. Шарыгин И.Ф., Голубев В.И. Факультативный курс по математике: Решение задач. Учеб. пособие для 11 класса средней школы. - М.: Просвещение, 1991. - 384 с.
9. [1] - Мордкович А. Г. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. – 11-е изд., стер. – М.: Мнемозина, 2009. – 215 с.
10. [2] – Алгебра: учеб. Для 8 кл. общеобразоват. Учреждений/[Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. – 16-е изд. – М. : Просвещение, 2008. – 271 с.
11. [3] - Мордкович А. Г. Алгебра и начала математического анализа. 11 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / А. Г. Мордкович, П. В. Семенов. – 2-е изд., стер. – М.: Мнемозина, 2008. – 287 с.
12. [4] - Алгебра и начала математического анализа. 10 класс : учеб. Для общеобразоват. Учреждений : базовый и профил. Уровни / [Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин]; под ред. А. Б. Жижченко. – 3-е изд. – М.: Просвещение, 2010.- 368 с.
Размещено на
Дата: 2019-11-01, просмотров: 191.
