Метод Гаусса состоит в применении к системе элементарных преобразований с целью получения лестничной системы. Рассмотрим систему (1). Будем считать, что каждое неизвестное встречается по крайней мере в одном уравнении с ненулевых коэффициентом. Тогда, при необходимости переставив уравнения, будем предполагать, что a₁₁≠0. Если k=1, то система является лестничной. Пусть k > 1. Исключим из уравнений 2,..., k неизвестное x₁. Для этого при i = 2, ... , k прибавим к i-му уравнению

1-е, умноженное на .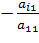

Получим систему

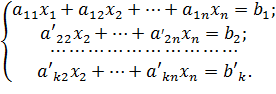        (3)

В силу леммы система (3) равносильна системе (1). Вычеркнем из нее все нулевые уравнения. Если полученная система содержит уравнение вида 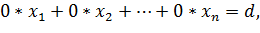где d≠0, то она несовместна, и вместе с ней несовместна система (1). Если после вычеркивания в системе остается более одного уравнения, то рассматриваем систему, полученную из последней системы отбрасыванием первого уравнения. В этой системе по крайней мере одно неизвестное встречается с ненулевым коэффициентом. Запишем ее, переставив уравнениям столбцы с неизвестными так, чтобы первый коэффициент был отличен от нуля.

Здесь 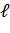≤ k, α₂₂≠0 и если столбцы с неизвестными переставлялись, то неизвестные перенумерованы так, что они идут по порядку.

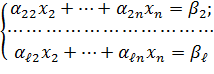            (4)

Если l=2, т.е. система (4) состоит из одного уравнения, то приведение к лестничной системе закончено. При l> 2 применим к системе (4) те же рассуждения, что и к системе (1), а именно исключим из 3, ... ,lуравнений неизвестное x₂, вычеркнем нулевые уравнения, проверим, совместна ли система. Продолжая этот процесс, мы либо установим несовместность системы (1), либо приведем ее к лестничной системе.

Пример 1.

Рассмотрим систему

Поскольку в лестничной системе в первом уравнении коэффициент при первом из неизвестных должен быть отличен от нуля, а в первом уравнении нашей системы коэффициент при x₁ равен нулю, выберем уравнение, в котором коэффициент при x₁ отличен от нуля, — например, второе, — и поменяем его местами с первым уравнением. Получим систему

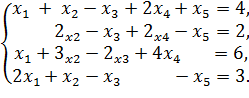
В лестничной системе во всех уравнениях, кроме первого, первое из неизвестных должно входить с коэффициентом 0. Чтобы добиться этого, прибавим к третьему уравнению системы первое, умноженное на −1, а к четвертому — первое, умноженное на −2. Получим систему

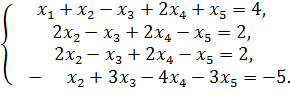
Дальнейшие преобразования применяются к системе, состоящей из трех последних уравнений (за исключением возможной перестановки столбцов с неизвестными). Поскольку в лестничной системе во всех уравнениях, кроме первых двух, второе из неизвестных должно входить с коэффициентом 0, прибавим к третьему уравнению последней системы второе уравнение, умноженное на −1, а затем умножим четвертое уравнение на 2 и к результату прибавим второе уравнение. Получается система

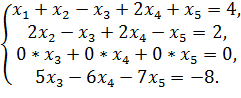
Вычеркивая из полученной системы третье уравнение, получаем лестничную систему

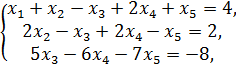              (6)

которая в силу леммы эквивалентна исходной системе. Легко понять, что система (6) совместна. Например, ее решением является набор чисел

(1, −1, 2, 3, 0).

Пример 2.

Рассмотрим следующую систему:

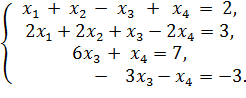            (7)

Прибавляя ко второму уравнению этой системы первое, умноженное на −2, получаем систему

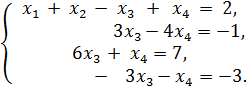
Столбец с неизвестным x₂ поставим на последнее место (это равносильно последовательному выполнению двух элементарных преобразований: сначала поменяем местами столбцы с неизвестными x₂ и x₄, а затем – столбцы с неизвестными x₄ и x₃). Получим:

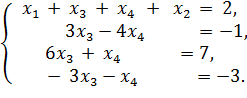
Прибавив к третьему уравнению второе, умноженное на −2, а к четвертому – второе (ни на что не умноженное), получаем:

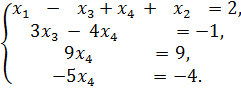
Если теперь к четвертому уравнению прибавить третье, умноженное на 5/9, то мы получим уравнение 0 · x₄ = 1. Следовательно, система (7) несовместна.

Критерий совместности в терминах элементарных преобразований

Из описания метода Гаусса, примем во внимание, что любая лестничная система совместна, получаем следующее утверждение.

Теорема

 Система линейных уравнений совместна тогда и только тогда, когда ее можно с помощью элементарных преобразований привести к лестничной системе.

2.2 Нелинейные преобразования систем уравнений

На итоговой аттестации по модернизированным программам, предлагаются задачи, в которых требуется решить системы алгебраических, нелинейных уравнений. Школьники испытывают большие затруднения, встречаясь с такими заданиями, особенно, если речь идет о нелинейных системах уравнений. Этот раздел алгебры по праву считается одним из трудных, так как нет единых способов решения систем алгебраических уравнений.

Необходимо помочь школьникам преодолеть трудности при решении алгебраических систем нелинейных уравнений, научить отыскивать наиболее рациональный способ решения систем уравнений, тем самым подготовить выпускника основной школы к сдаче экзамена по математике, продолжению образования в выпускных классах средней школы с профильным обучением, а затем в вузе, где дисциплины математического цикла являются профильными.

Предлагаются некоторые способы решения нелинейных систем уравнений. Причем, среди предлагаемых примеров имеются, как достаточно простые, так и сложные.

При решении систем уравнений применяются различные методы:

1. разложение на множители;

2. исключение переменных;

3. алгебраическое сложение;

4. замена переменных;

5. системы однородных уравнений;

6. метод введения новых переменных;

7. графический метод.

Рассмотрим некоторые методы решения нелинейных систем уравнений.