Система линейных уравнений называется совместной, если она имеет по крайней мере одно частное решение (т.е. ее общее решение не пусто); в противном случае говорят, что система несовместна.

Система, имеющая единственное решение, называется определенной, а система, имеющая более одного решения, – неопределенной.

Система линейных уравнений называется однородной, если свободные члены во всех уравнениях равны нулю. Однородная система линейных уравнений всегда совместна, так как имеет нулевое решение (0, 0, ... , 0).

Две системы линейных уравнений называются равносильными, если они имеют совпадающие общие решения. Это означает, что каждое частное решение первой системы является решением второй и, обратно, каждое частное решение второй системы будет решением первой. Любые две несовместные системы по определению равносильны.

Элементарные преобразования системы линейных уравнений

Элементы поля для краткости будем называть скалярами.

Следующие преобразования системы линейных уравнений называются элементарными:

1) умножение уравнения на ненулевой скаляр;

2) прибавление одного уравнения, умноженного на скаляр, к другому;

3) перестановка двух уравнений;

4) перестановка двух столбцов с неизвестными;

5) вычеркивание уравнений вида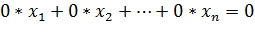

Уравнение вида 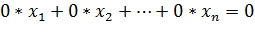 будем называть нулевым.

Обоснование метода Гаусса

Следующая лемма играет ключевую роль в обосновании метода Гаусса. Лемма:

Элементарные преобразования системы линейных уравнений сохраняют множество ее решений, т.е. приводят к равносильной системе.

Тот факт, что множество решений системы сохраняется преобразованиями 3–5, очевиден. Очевидно также, что если верное равенство умножить на любой скаляр, то оно останется верным. Поэтому решение данной системы является и решением системы, полученной из нее умножением одного из уравнений на ненулевой скаляр t. Поскольку исходная система получается из новой преобразованием такого же типа (умножением того же уравнения на скаляр 1/t), всякое решение новой системы является и решением исходной системы. Таким образом, преобразование 1 также не меняет множества решений системы.

Пусть теперь новая система получена из старой прибавлением j-того уравнения, умноженного на скаляр t, к i-тому. Поскольку если верное равенство умножить на любой скаляр t, то оно останется верным и сумма двух верных равенств – снова верное равенство, всякое решение старой системы является и решением новой. Далее, старую систему можно получить из новой последовательным выполнением трех преобразований – сначала умножаем j-тое уравнение новой системы (совпадающее с j-тым уравнением старой системы!) на −t, затем прибавляем полученное уравнение к i-тому уравнению новой системы. В силу сказанного выше, всякое решение новой системы является и решением старой. Таким образом, и преобразование 2 не меняет множества решений системы. Лемма доказана.