Решая уравнение, мы стремимся преобразовать его к более простому виду. Не забывая при этом следить за тем, чтобы более простое уравнение оставалось равносильным исходному.

Правила равносильных преобразований:

1. Если в уравнении какое-нибудь слагаемое перенести из одной части в другую, изменив его знак, то получится уравнение равносильное данному.

2. Если обе части уравнения умножить или разделить на одно и то же число, отличное от нуля, то получится уравнение, равносильное данному.

Пример.

Найти корень уравнения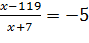

Это уравнение относится к типу дробно-рациональных. Наиболее простой вид подобных уравнений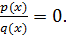

Так как, если дробь равна нулю, то числитель равен нулю, а знаменатель должен существовать и не может быть равен нулю, потому что на нуль делить нельзя. Это нужно учитывать, чтобы избавиться от посторонних корней.

Решение.

1) Преобразуем дробь к простому виду.

Для этого перенесем все в правую часть, затем приведем дробь к общему знаменателю.

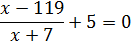
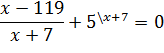
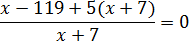
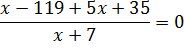
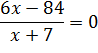
2) Числитель дроби приравниваем к нулю:

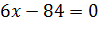
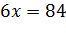
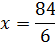
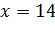
3) Так как знаменатель представляет собой многочлен (в данном случае линейный двучлен), то он существует при любых значениях переменной. Поэтому для знаменателя достаточно потребовать того, чтобы он не равнялся нулю

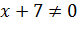
Далее выбираем, что проще,

· Подставить в последнее неравенство x=14, чтобы убедится, что предполагаемый корень не является «ложным»:

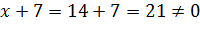
· Решить противоположное уравнение, чтобы затем отбросить совпадающие для числителя и знаменателя корни:

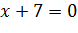
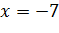
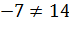
4) Делаем вывод – значение переменной x=14, которое обращает числитель в 0, и есть искомый корень уравнения.

5) Прежде, чем записать ответ, нужно сделать проверку.

6) Берем исходное условие задачи.

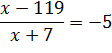
7) Вместо xподставляем наш ответ:14

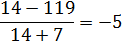
8) Вычисляем числовые значения каждой части равенства отдельно. В этом примере в правой части уже стоит число, поэтому вычислим только левую часть.

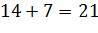
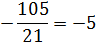
9) Так как -5=-5, то x=14 является корнем уравнения, и можно записать ответ.

Ответ:14.

Глава II . Основные преобразования систем уравнений

2.1 Линейные преобразования систем уравнений

Современная алгебра, как наука, представляет собой обширный раздел математики, состоящий из большого числа дисциплин (теория групп, колец, полей, линейная алгебра и т.д.). Предметом изучения современной алгебры являются операции, обладающие некоторыми, вполне определенными свойствами, и множества, над элементами которых установлены эти операции (кольца, поля, группы).

Определение: Пусть F – поле. Система k линейных алгебраических уравнений с n неизвестными над полем F может быть записана так:

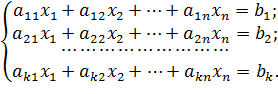                 (1)

Здесь a_ij∈ F (i = 1, 2, . . . , k, j = 1, 2, . . . , n) называются коэффициентами системы (1), b_i∈ F (i = 1, 2, . . . , k) — ее свободными членами. Они предполагаются известными.

Частным решением системы линейных уравнений (1) называется упорядоченный набор (c₁, c₂,...,c_n) элементов из F, такой, что при подстановке в каждое ее уравнение вместо неизвестных x₁, x₂, ... , x_n элементов c₁, c₂, ... , c_n соответственно это уравнение превращается в верное равенство.

Решить систему (1) означает указать определенным способом все ее частные решения или доказать, что их не существует. Множество всех частных решений данной системы линейных уравнений называется ее общим решением.

Например, для системы линейных уравнений над полем R

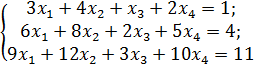
строка (−1, 0, 0, 2) является частным решением, а строка (1, −1, −1, 2) – не является.