Система двух уравнений с двумя переменными вида
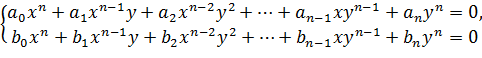
называется однородной (левые части обоих уравнений однородные многочлены степени n от двух переменных).
Однородные системы решаются комбинацией двух методов: линейного преобразования и введения новых переменных.
Пример 5. Решить систему 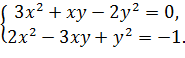
Решение.
Первое уравнение системы однородное (напомним, что уравнение вида 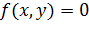 , где
, где 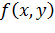 - однородный многочлен - называется однородным уравнением). Заметим, что если положить y=0 то из однородного уравнения
- однородный многочлен - называется однородным уравнением). Заметим, что если положить y=0 то из однородного уравнения 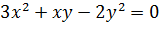 находим x=0. Но пара чисел (0;0) не удовлетворяет второму уравнению системы, поэтому y≠0 и, следовательно, обе части однородного уравнения
находим x=0. Но пара чисел (0;0) не удовлетворяет второму уравнению системы, поэтому y≠0 и, следовательно, обе части однородного уравнения 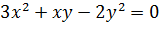 можно разделить на y2 (это не приведёт к потере корней).
можно разделить на y2 (это не приведёт к потере корней).
Получим 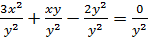 и
и 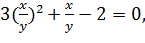 откуда находим, что
откуда находим, что 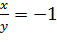 или
или 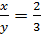 , то есть
, то есть 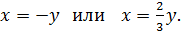
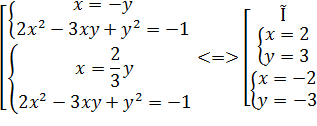
Ответ: {(2; 3), (-2;-3)}.
Типичные ошибки при решении систем и методы их устранения
При решении некоторых систем иногда происходит потеря корней в ответе или появляются посторонние корни. Основная причина этого заключается в том, что осуществляются правдоподобные рассуждения, но теряется контроль над равносильностью переходов от одной системы к другой. Для того чтобы избежать подобных ошибок, нужно знать природу их появления и на определенном этапе решения произвести необходимые преобразования, проверку решения и т.д.
В качестве таких примеров рассмотрим решение нескольких систем нелинейных уравнений.
Пример 6. Решите систему уравнений 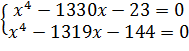
Неправильное решение.
Вычтем из первого уравнения системы второе уравнение. Получим
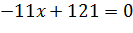 , откуда x =11.
, откуда x =11.
В этом случае корень уравнения, полученный после эквивалентного преобразования (вычли второе уравнение из первого), не проверили. Чтобы избежать подобной ошибки, необходимо после вычитания одного уравнения из другого решать систему уравнений, в которой обязательным является наличие уравнения, полученное после вычитания и одного из первоначальных уравнений.
Неправильный ответ: {11}.
Правильное решение.
Выполним эквивалентные преобразования: 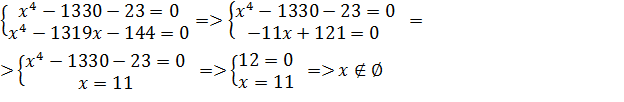
Таким образом, при решении системы уравнений, необходимо записать такое же количество уравнений, которое было в условии, чтобы не получить посторонний корень.
Правильный ответ: 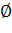 .
.
Глава III . Основные преобразования логарифмических неравенств
Основные свойства логарифма
Слово «логарифм» происходит от греческих слов «αριθμος» - число и «λογοσ» - отношение. Переводится как «отношение чисел», одно из которых является членом арифметической прогрессии, а другое – геометрической.
Определение: логарифмом положительного числа b по основанию a (a >0, a≠1)называется показатель степени, в которую нужно возвести a, чтобы получить b.
Обозначение логарифма: 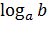 .
.
Пример 1.
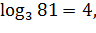 так как 34=81;
так как 34=81;
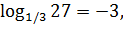 так как (1/3) -3 = 33 = 27.
так как (1/3) -3 = 33 = 27.
Вышеприведенное определение логарифма можно записать следующим образом: 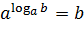
Полученное равенство называют основным логарифмическим тождеством.
Пример 2.
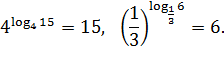
Операцию нахождения логарифма числа называют логарифмированием.
Выделим три формулы:
1. 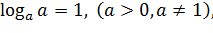
2. 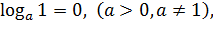
3. 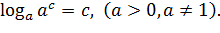
Свойства логарифмов
1. Логарифм произведения равен сумме логарифмов множителей (с>0, c≠0, a>0, b>0)
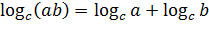
Пример.
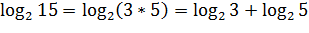
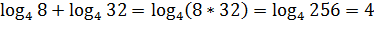
2. Логарифм частного равен разности логарифмов делимого и делителя (с>0, c≠1, a>0, b>0)
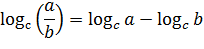
Пример.
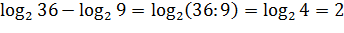
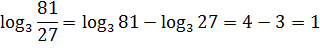
3. Логарифм степени равен произведению показателя степени на логарифм её основания (с>0, c≠1, b>0)
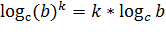
Пример.
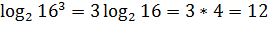
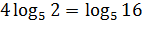
Следствием этого свойства является следующее утверждение: логарифм корня равен логарифму подкоренного числа, делённому на степень корня:
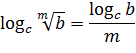
4. Если в основании логарифма находится степень, то величину, обратную показателю степени, можно вынести за знак логарифма:
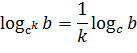
Два последних свойства можно объединить в одно:
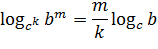
Формула перехода от одного основания логарифма к другому основанию (с>0, c≠1, a>0, a≠1,b>0)
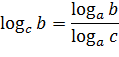
Пример.
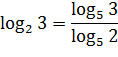
В частном случае при b=aимеем:
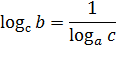
Пример.
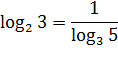
Дата: 2019-11-01, просмотров: 329.