Содержание
Введение................................................................................................... 3
Глава I. Равносильные преобразования уравнений.............................. 4
1.1 Понятие равносильных уравнений.......................................... 4
1.2 Понятие уравнений-следствий.................................................. 7
1.3 Решение простых уравнений из заданий ЕГЭ......................... 8
Глава II. Основные преобразования систем уравнений....................... 11
2.1 Линейные преобразования систем уравнений...................... 11
2.2 Нелинейные преобразования систем уравнений................... 18
Глава III. Основные преобразования логарифмических неравенств.. 26
3.1 Основные свойства логарифма.............................................. 26
3.2 Методы решения логарифмических неравенств................... 29
3.3 Решение логарифмических неравенств из профильного ЕГЭ 31
Заключение............................................................................................. 35
Список используемой литературы........................................................ 36
Введение
В процессе решения уравнений, неравенств либо систем, предлагаемых в школьном курсе математики, учащимися средней школы нередко допускаются ошибки, влекущие за собой потерею некоторых решений или нахождение «посторонних» решений. Другими словами, в результате в ответ записывается множество, отличное от множества решений данного уравнении, неравенства или системы, и задача признается решено неверно. Ошибки такого типа чаще всего связаны с неравносильными переходами от одного уравнения (неравенства, системы) к другому. В данной курсовой работе будут рассмотрены несколько приемов, использование которых обеспечивает сохранение множества решений исходного уравнения (неравенства, системы) в процессе его решения.
Глава I . Равносильные преобразования уравнений
Понятие уравнений-следствий
Процитируем несколько примеров определений уравнений-следствий, взятых из учебных пособий.
Определение: Следствием уравнения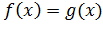 
будет уравнение 
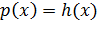при условии, что каждый корень первого уравнения будет в то же время корнем второго [3].
Определение: Если первое уравнение имеет те же корни, что и второе, то второе будет уравнением-следствием первого [4].
Возьмем несколько примеров таких уравнений.
Пример 3.
Уравнение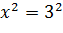 
является следствием уравнения 
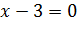, поскольку второе уравнение имеет единственный корень х=3, этот корень является и корнем уравнения 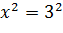, поэтому по определению уравнение 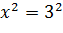– это следствие уравнения 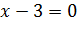. Еще один пример: уравнение 
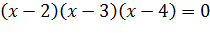будет следствием 
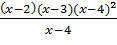, потому что второе уравнение имеет два корня, равные 2 и 3, которые в то же время будут корнями первого.
Из данного выше определения можно сделать вывод, что следствием любого уравнения, не имеющего корней, будет также любое уравнение. Приведем несколько очевидных следствий из определения равносильных уравнений и определения уравнения – следствия:
1. Если одно уравнение равносильно другому, то каждое из них будет следствием другого.
2. Если из двух уравнений каждое будет следствием другого, то данные уравнения будут равносильны друг другу.
3. Уравнения будут равносильны по отношению друг к другу только в том случае, если каждое из них будет следствием другого.
Обоснование метода Гаусса
Следующая лемма играет ключевую роль в обосновании метода Гаусса. Лемма:
Элементарные преобразования системы линейных уравнений сохраняют множество ее решений, т.е. приводят к равносильной системе.
Тот факт, что множество решений системы сохраняется преобразованиями 3–5, очевиден. Очевидно также, что если верное равенство умножить на любой скаляр, то оно останется верным. Поэтому решение данной системы является и решением системы, полученной из нее умножением одного из уравнений на ненулевой скаляр t. Поскольку исходная система получается из новой преобразованием такого же типа (умножением того же уравнения на скаляр 1/t), всякое решение новой системы является и решением исходной системы. Таким образом, преобразование 1 также не меняет множества решений системы.
Пусть теперь новая система получена из старой прибавлением j-того уравнения, умноженного на скаляр t, к i-тому. Поскольку если верное равенство умножить на любой скаляр t, то оно останется верным и сумма двух верных равенств – снова верное равенство, всякое решение старой системы является и решением новой. Далее, старую систему можно получить из новой последовательным выполнением трех преобразований – сначала умножаем j-тое уравнение новой системы (совпадающее с j-тым уравнением старой системы!) на −t, затем прибавляем полученное уравнение к i-тому уравнению новой системы. В силу сказанного выше, всякое решение новой системы является и решением старой. Таким образом, и преобразование 2 не меняет множества решений системы. Лемма доказана.
Метод замены переменных
Метод замены неизвестных основан на следующем утверждении.
Пусть дана система уравнений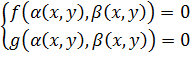 
(1)
и пусть дана система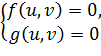 
имеет kразличных решений (u1,v1); (u2,v2); … (uk,vk).
Тогда система (1) равносильна совокупности kсистем
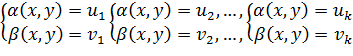
Пример 4. Решить систему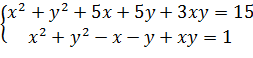 
Решение.
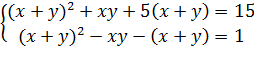
Произведем замену.
Пусть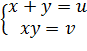 
, тогда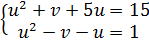 
Складывая уравнения, получим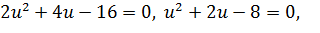 
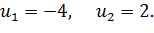
Преобразуем первое уравнение:
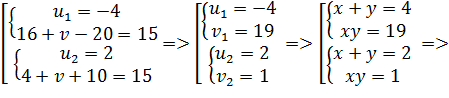
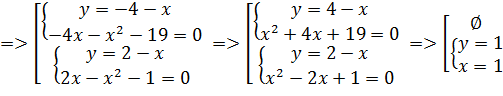
Ответ: {(1; 1)}
Основные свойства логарифма
Слово «логарифм» происходит от греческих слов «αριθμος» - число и «λογοσ» - отношение. Переводится как «отношение чисел», одно из которых является членом арифметической прогрессии, а другое – геометрической.
Определение: логарифмом положительного числа b по основанию a (a >0, a≠1)называется показатель степени, в которую нужно возвести a, чтобы получить b.
Обозначение логарифма: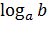 
.
Пример 1.
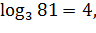так как 34=81;
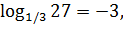так как (1/3) -3 = 33 = 27.
Вышеприведенное определение логарифма можно записать следующим образом: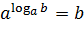 
Полученное равенство называют основным логарифмическим тождеством.
Пример 2.
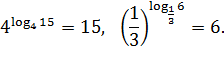
Операцию нахождения логарифма числа называют логарифмированием.
Выделим три формулы:
1. 
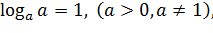
2. 
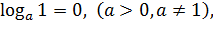
3. 
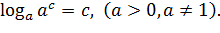
Свойства логарифмов
1. Логарифм произведения равен сумме логарифмов множителей (с>0, c≠0, a>0, b>0)
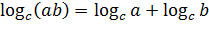
Пример.
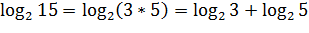
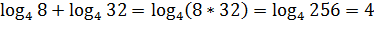
2. Логарифм частного равен разности логарифмов делимого и делителя (с>0, c≠1, a>0, b>0)
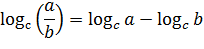
Пример.
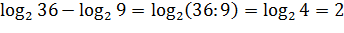
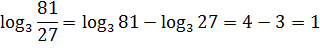
3. Логарифм степени равен произведению показателя степени на логарифм её основания (с>0, c≠1, b>0)
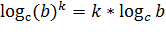
Пример.
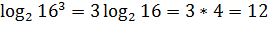
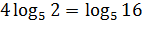
Следствием этого свойства является следующее утверждение: логарифм корня равен логарифму подкоренного числа, делённому на степень корня:
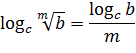
4. Если в основании логарифма находится степень, то величину, обратную показателю степени, можно вынести за знак логарифма:
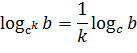
Два последних свойства можно объединить в одно:
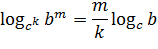
Формула перехода от одного основания логарифма к другому основанию (с>0, c≠1, a>0, a≠1,b>0)
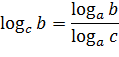
Пример.
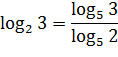
В частном случае при b=aимеем:
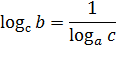
Пример.
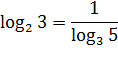
Заключение
В данной работе была кратко приведена основная теоретическая информация, необходимая для решения уравнений, неравенств и систем. Помимо этого, были рассмотрены некоторые общие приемы решения таких уравнений, неравенств и систем, и приведены примеры решения. Следует отметить, что эти примеры часто вызывают затруднения у школьников при подготовке к Единому государственному экзамену по математике. Это, в свою очередь, требует повышенного внимания к данной теме.
Уравнения, неравенства и системы встречаются учащимся, как при решений заданий частиB, так и при решении заданий уровня повышенной сложности, встречающихся в части С. В последнем случае, задания требуют от учащихся уверенных навыков решения, и наиболее рационально подходить к решению этих заданий в рамках функционального метода решения уравнений, неравенств и систем.
Список используемой литературы
1. В. А. Гусев, А. Г. Мордкович «Математика. Справочные материалы», Книга для учащихся, М.: «Просвещение», 1990 г.2. Л.О.Денищев, Е. М.Бойченко и др. «Готовимся к единому государственному экзамену», Математика, Изд. «Дрофа», 2004 г.3. Ф. Ф.Лысенко, В. Ю.Калашников «Подготовка к ЕГЭ поматематике», Ростов-на-Дону, 2002 г.
4. Азаров А.И., Барвенов С.А., Федосенко В.С., Шибут А.С. Системы алгебраических уравнений. Текстовые задачи. Справочное пособие для абитуриентов и школьников. 1998. - 288 с.
5. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 11 класса. Учеб. пособие для учащихся шк. и классов с углубл. изуч. математики. 4-е изд. - М.: Просвещение, 1995. - 335 с.
6. Галицкий М.Л., Гольдман А.М., Звавич Л.И. Сборник задач по алгебре для 8-9 классов. Учеб. пособие для учащихся шк. и классов с углубл. изуч. курса математики. М.: Просвещение, 1992. - 271 с.
7. Самусенко А.В., Казаченок В.В. Математика: Типичные ошибки абитуриентов. 2-е изд., испр. - Мн.: Выш. шк., 1995.- 185 с.
8. Шарыгин И.Ф., Голубев В.И. Факультативный курс по математике: Решение задач. Учеб. пособие для 11 класса средней школы. - М.: Просвещение, 1991. - 384 с.
9. [1] - Мордкович А. Г. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. – 11-е изд., стер. – М.: Мнемозина, 2009. – 215 с.
10. [2] – Алгебра: учеб. Для 8 кл. общеобразоват. Учреждений/[Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. – 16-е изд. – М. : Просвещение, 2008. – 271 с.
11. [3] - Мордкович А. Г. Алгебра и начала математического анализа. 11 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / А. Г. Мордкович, П. В. Семенов. – 2-е изд., стер. – М.: Мнемозина, 2008. – 287 с.
12. [4] - Алгебра и начала математического анализа. 10 класс : учеб. Для общеобразоват. Учреждений : базовый и профил. Уровни / [Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин]; под ред. А. Б. Жижченко. – 3-е изд. – М.: Просвещение, 2010.- 368 с.
Размещено на
Содержание
Введение................................................................................................... 3
Глава I. Равносильные преобразования уравнений.............................. 4
1.1 Понятие равносильных уравнений.......................................... 4
1.2 Понятие уравнений-следствий.................................................. 7
1.3 Решение простых уравнений из заданий ЕГЭ......................... 8
Глава II. Основные преобразования систем уравнений....................... 11
2.1 Линейные преобразования систем уравнений...................... 11
2.2 Нелинейные преобразования систем уравнений................... 18
Глава III. Основные преобразования логарифмических неравенств.. 26
3.1 Основные свойства логарифма.............................................. 26
3.2 Методы решения логарифмических неравенств................... 29
3.3 Решение логарифмических неравенств из профильного ЕГЭ 31
Заключение............................................................................................. 35
Список используемой литературы........................................................ 36
Введение
В процессе решения уравнений, неравенств либо систем, предлагаемых в школьном курсе математики, учащимися средней школы нередко допускаются ошибки, влекущие за собой потерею некоторых решений или нахождение «посторонних» решений. Другими словами, в результате в ответ записывается множество, отличное от множества решений данного уравнении, неравенства или системы, и задача признается решено неверно. Ошибки такого типа чаще всего связаны с неравносильными переходами от одного уравнения (неравенства, системы) к другому. В данной курсовой работе будут рассмотрены несколько приемов, использование которых обеспечивает сохранение множества решений исходного уравнения (неравенства, системы) в процессе его решения.
Глава I . Равносильные преобразования уравнений
Понятия равносильных уравнений
Определение: Равносильными называются такие уравнения, имеющие одни и те же корни, или же те, в которых корней нет.
Определения такого типа часто встречаются в различных учебниках. Приведем несколько примеров.
Определение: Уравнение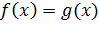 
считается равносильным уравнению 
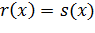, если они имеют одинаковые корни или если оба уравнения не имеют корней [1].
Определение: Уравнения, имеющие одни и те же корни, называют равносильными уравнениями. Уравнения, не имеющие корней, также считают равносильными [2].
Определение: Если уравнение 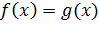имеет то же множество корней, что и уравнение 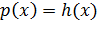, то они считаются равносильными по отношению друг к другу[3].
Под одними и теми же корнями понимается следующее: если какое-то число является корнем одного из равносильных уравнений, то оно является и корнем любого другого из этих уравнений, и не одно из равносильных уравнений не может иметь корня, который не является корнем любого другого из этих уравнений.
Приведем несколько примеров таких уравнений.
Пример 1.
Например, равносильными будут
,
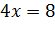
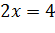
поскольку каждое из них имеет только один корень – двойку. Также равносильными будут
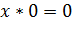и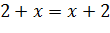 
,
поскольку их корнями могут быть любые числа, то есть множества их решений совпадают. Также равносильными будут уравнения
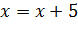и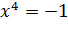 
,
каждое из которых не имеют действительных решений.
Для наглядности рассмотрим несколько примеров неравносильных уравнений.
Пример 2.
К примеру, таковыми будут
и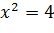 
,
поскольку их корни отличаются, так как второе уравнение имеет корень -2, который не является корнем первого уравнения. То же относится и к уравнениям
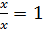и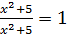 
,
так как корнями второго уравнения являются любые числа, а 0 не является корнем первого уравнения.
Озвученное определение равносильных уравнений относится как к уравнениям с одной переменной, так и к уравнениям с большим числом переменных. Однако для уравнений с двумя, тремя и т.д. переменными слово «корни» в определении нужно заменить словом «решения».
Определение: Равносильные уравнения – это уравнения, имеющие одни и те же решения, или не имеющие их.
Возьмем примеры уравнений, которые содержат несколько переменных и являются равносильными друг другу.
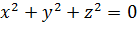и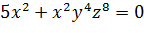 
Это равносильные уравнения с тремя переменными x, y, z, они оба имеют единственное решение (0, 0, 0). А уравнения с двумя переменным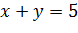и
и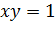 
не являются равносильными, так как пара значений x=2, y=3 является решением первого уравнения (при подстановке этих значений в первое уравнение получаем верное равенство 2+3=5), но не является решением второго (при подстановке этих значений во второе уравнение получаем неверное равенство 2*3=1).
Понятие уравнений-следствий
Процитируем несколько примеров определений уравнений-следствий, взятых из учебных пособий.
Определение: Следствием уравнения 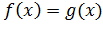будет уравнение 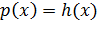при условии, что каждый корень первого уравнения будет в то же время корнем второго [3].
Определение: Если первое уравнение имеет те же корни, что и второе, то второе будет уравнением-следствием первого [4].
Возьмем несколько примеров таких уравнений.
Пример 3.
Уравнение 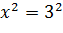является следствием уравнения 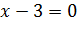, поскольку второе уравнение имеет единственный корень х=3, этот корень является и корнем уравнения 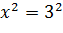, поэтому по определению уравнение 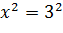– это следствие уравнения 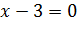. Еще один пример: уравнение 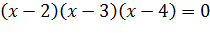будет следствием 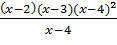, потому что второе уравнение имеет два корня, равные 2 и 3, которые в то же время будут корнями первого.
Из данного выше определения можно сделать вывод, что следствием любого уравнения, не имеющего корней, будет также любое уравнение. Приведем несколько очевидных следствий из определения равносильных уравнений и определения уравнения – следствия:
1. Если одно уравнение равносильно другому, то каждое из них будет следствием другого.
2. Если из двух уравнений каждое будет следствием другого, то данные уравнения будут равносильны друг другу.
3. Уравнения будут равносильны по отношению друг к другу только в том случае, если каждое из них будет следствием другого.
Дата: 2019-11-01, просмотров: 207.
